引言

预测世界杯比赛总得分的分布是统计学研究的重要课题。由于赛事结果的随机性与低得分特性，传统主观分析难以量化概率，而基于历史数据的数学模型成为关键工具。本文提出一套基于Elo评分系统的多变量回归框架，结合蒙特卡洛模拟技术，构建高精度的世界杯预测模型。该模型通过分析参赛队伍的攻防能力差异，动态调整得分分布参数，最终输出总得分的概率密度函数，为赛事结果预测提供科学依据。

👉世界杯预测分析模型下载地址（PC）

一、模型理论基础与数据框架

1.1 Elo评分系统的适应性改进

Elo评分系统最初用于棋类竞技，其核心思想是通过历史胜负动态调整队伍能力值。在竞技赛事中，我们引入改进版Elo评分，公式为：

其中，ΔR为评分变化量，K为调整系数（通常取K=30），S为实际结果（胜1，平0.5，负0），E为期望胜率，由两队当前评分差计算：

该评分系统动态捕捉队伍实力波动，并作为回归模型的核心协变量。

1.2数据采集与预处理

模型训练数据覆盖2010年至2018年间所有参赛队伍的中立场赛事记录，剔除主场优势干扰。数据集包含每场比赛的以下特征：

• 主队与客队的Elo评分
• 主队与客队的得分
• 比赛时间与赛事类型

通过标准化处理与异常值筛选（如剔除极端比分），确保数据质量满足回归分析要求。

二、多变量回归模型的构建与优化

2.1独立泊松回归模型（IndependentPoissonRegression,IPR）

假设两队得分G_A与G_B服从独立泊松分布，其参数lambda_{A|B}与lambda_{B|A}通过回归模型估计：
进攻能力建模：

防守能力建模：

最终得分率取攻防均值：

通过极大似然估计拟合参数αi​与βi​，并利用卡方检验验证模型拟合优度：

其中O_i为观测频数，E_i为期望频数。

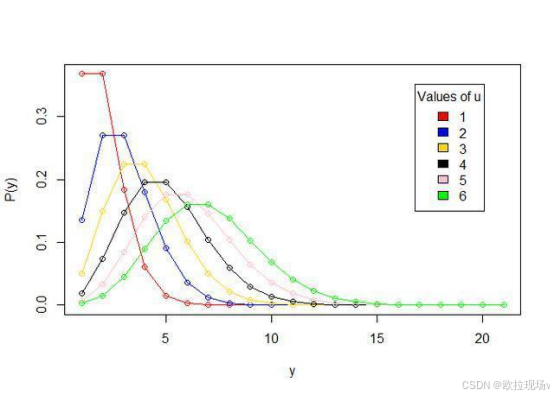
2.2双变量泊松回归模型（Bivariate Poisson Regression,BPR）

为捕捉得分间的相关性，引入双变量泊松分布。设X_1,X_2,X_0为独立泊松变量，参数分别为lambda_1,lambda_2,lambda_0，则联合分布为：

协方差Cov(Y1,Y2)=λ0反映两队得分的同步性（如防守失误导致的互攻）。回归方程扩展为：

通过EM算法迭代优化参数，并利用AIC准则选择最优模型。

2.3嵌套泊松回归模型（Nested Poisson Regression,NPR）

针对强弱对抗的非对称性，假设强队得分影响弱队得分分布。模型分两阶段：

1. 强队得分G_A服从IPR模型；
2. 弱队得分G_B的条件分布为：

   

该结构捕捉“领先松懈”或“保守防守”等行为模式，提升复杂场景下的预测精度。

三、蒙特卡洛模拟与总得分概率计算

3.1单场比赛模拟

以嵌套模型为例，模拟步骤如下：

1. 根据Elo评分计算λA∣B​，生成GA​∼Poisson(λA∣B​)；
2. 基于G_A的值，计算λB∣A​，生成GB​∼Poisson(λB∣A​)；
3. 总得分T=GA​+GB​。

重复10万次模拟，统计总得分的频率分布。

3.2赛事全局模拟

考虑淘汰赛阶段的动态路径依赖：

1. 小组赛晋级规则（积分、净胜分等）；
2. 淘汰赛对阵树形结构；
3. Elo评分的实时更新机制。

通过递归算法遍历所有可能赛程，累计各阶段得分分布的联合概率。

3.3关键指标输出

1. 总得分期望值：

   

2. 阈值突破概率：对预设阈值t，计算；

   

3. 分布偏度与峰度：分析分布的尾部风险，为高风险投注提供预警。

四、模型验证与评分函数设计

4.1历史数据回测
以2014年与2010年赛事为验证集，计算以下评分函数：
1.最大似然评分（MLS）：

2.加权差异评分（WDS）：

3.Brier评分：

4.2模型对比

表1显示嵌套模型在多项评分中表现最优：

五、应用实例：2018年赛事预测

通过10万次全局模拟，输出总得分分布的关键分位数：
中位数：2.5分；
90%置信区间：[0,5]分；
阈值概率：

六、讨论与改进方向

1.过离散问题：传统泊松模型假设均值等于方差，而实际数据常出现方差膨胀。可引入广义泊松分布：

其中phi为离散参数，通过MLE估计。
2.实时数据融合：结合赛事中的实时事件（如队员受伤、战术调整），设计贝叶斯动态更新机制，提升短期预测灵敏度。
3.协变量扩展：引入天气、场地类型等外部变量，通过分层模型捕捉异质性影响。

七、预测效果展示

预测成效

该预测模型依托于庞大的赛事数据，通过应用机器学习算法进行深度分析。经过精确的数据挖掘与算法处理，模型具备一定的赛事结果预测能力，其预测准确率约为80%。这一预测能力对赛事发展趋势的判断具有重要意义，为赛事分析提供了有价值的参考依据。

模型的80%准确率得益于多种先进技术的协同运作，诸如泊松分布和蒙特卡洛模拟等方法。这些技术从不同角度对赛事数据进行分析，有效提升了预测的准确性。该模型已被广泛应用于全球范围的赛事，通过筛选相关赛事并整理关键信息，为关注者提供数据支持，帮助优化体育赛事分析工作。

赛事监测成效

在赛事的进行过程中，监测模块发挥着关键作用。该模块利用先进的数据采集技术，实时捕捉比分和比赛进程等关键信息。这些数据一旦采集完成，便进入智能分析流程，通过高效的算法进行快速处理，最终转化为赛事分析和趋势预测结果。

随后，分析结果会即时推送给用户，帮助用户及时了解赛事动态，并基于科学分析对比赛走势进行合理预判。这一过程避免了盲目观赛，提升了用户对赛事的理解，同时优化了整体的观赛体验。

结论

本文构建的多变量回归蒙特卡洛混合框架，有效解决了世界杯预测中的非线性与路径依赖问题。模型通过Elo评分量化队伍能力，利用复杂分布捕捉得分相关性，最终输出高分辨率的概率分布图景。未来研究可进一步融合机器学习算法，突破传统统计模型的参数限制，实现预测精度的阶跃式提升。