差分方程模型系列：

差分方程模型（一）：模型介绍与Z变换

差分方程模型(二）：蛛网模型

差分方程模型(三）： 预测商品销售量

差分方程模型(四）：遗传模型

---

差分方程是包含未知函数的差分及自变数的方程。在求微分方程的数值解时，常用差分来近似微分，所导出的方程就是差分方程。通过解差分方程来求微分方程的近似解，是连续问题离散化的一个例子。

离散状态转移模型涉及的范围很广，可以用到各种不同的数学工具。下面我们对差 分方程作一简单的介绍，下一章我们将介绍马氏链模型。

目录

1 差分方程简介

 n 阶常系数线性差分方程及求解                  两个例题                              解的稳定性

2 常系数线性差分方程的 Z 变换解法

2.1 几个常用离散函数的 Z 变换            

2.2    Z 变换的性质

（i）线性性质                               （ii）平移性

---

1 差分方程简介

满足一差分方程的序列 称为差分方程的解。类似于微分方程情况，若解中含有 的独立常数的个数等于差分方程的阶数时，称此解为该差分方程的通解。若解中不含任 意常数，则称此解为满足某些初值条件的特解。

 n 阶常系数线性差分方程及求解

两个例题

 

解的稳定性

程（1）稳定的充要条件为其所有特征根的模均小于 1。

 

2 常系数线性差分方程的 Z 变换解法

常系数线性差分方程采用解析解法比较容易，而且对其解的意义也容易理解，但采 用这种解法求解常系数线性非齐次差分方程比较繁琐，通常是采用 Z 变换，将差分方 程变换为代数方程去求解。

2.1 几个常用离散函数的 Z 变换

（i）单位冲激函数δ (k) 的 Z 变换

（ii）单位阶跃函数U(k) 的 Z 变换

（iii）单边指数函数   的 Z 变换（a 为不等于 1 的正常数）

2.2    Z 变换的性质

（i）线性性质

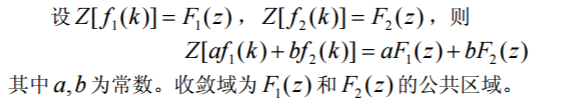
（ii）平移性

例 3  求齐次差分方程

---

差分方程模型系列：

差分方程模型（一）：模型介绍与Z变换

差分方程模型(二）：蛛网模型

差分方程模型(三）： 预测商品销售量

差分方程模型(四）：遗传模型

 

---