电力拖动系统——交流调速系统

总结内容：
三相异步电动机的起动、调速、制动、变压变频调速、SPWM、SVPWM 、CHBPWM调制、VC系统、FOC系统、DTC系统、3/2变换、2r/2s变换、双馈调速、串级调速。

---

提示：本文章是本人结合所学的课程进行总结所写，如果大家感兴趣，直接从目录里找需要的看。本文很长，切忌一口气读完

---

前言

简介：

大家好，接着之前的直流调速，现在我开始总结电力拖动系统中交流调速系统部分。截止到目前为止，算上这篇，数了数我已经写了16篇关于大学知识点总结的文章了，总算是在硬件部分把知识点总结了个遍，虽然还是没找到写这些文章的意义……但最起码感觉对得起自己这几个月以来的付出，今天我将进行本次大规模更新文章的最后一章，也是大学里关于硬件部分的最后一篇。作为电气专业，电力拖动系统可以说是我们的专业课中的必修课程，同时也是我学的最好的、最具有分量的几个课程之一（主要是老师教的好，(^▽)在此特别特别感谢赵红老师对我们的教导），正是因为它尤其的重要，所以我决定好好研究研究。以下便是我对直流调速系统所学知识的理解与总结。

本人学艺不精，有一些知识点地方可能存在瑕疵，希望各位大佬可以多多指教。

---

以下是本篇文章正文内容：

第一章——异步电动机变压调速系统

一、三相异步电动机的起动

与直流电动机相同，我们希望在起动时有较大起动转矩，较小起动电流。
改善起动性能的方法：笼型：采用特殊结构的转子（深槽、双鼠笼）；绕线型：转子串入附加电阻。

1.笼型异步电动机的降压起动

降压起动方法：起动时，施加低于额定值的定子电压。电动机的转速上升到接近额定转速后，再切换到额定电压下运行。
特点：起动电流下降，且起动转矩亦下降
应用：适用于对起动转矩要求不高的场合，如风机、离心泵等
（1） 自耦变压器降压起动

（2） Y-Δ 起动
适用于在正常运行时定子绕组按三角形连接的电机。起动时，使定子绕组为星形连接，待转速上升到额定转速后，再换接成三角形连接。
（3）定子串电抗器或电阻起动
串电阻降压：电阻消耗能量，电机效率低，适合小容量。
定子串电抗(电阻)起动特点：简单，但起动性能效果较差

2.线绕型异步电动机的起动

（1）转子回路串电阻分级起动
转子回路中通过集电环串入附加电阻，限制起动电流，提高起动转矩。起动后把附加电阻切除，使正常运行有较高效率。
（2）转子回路串频敏变阻器起动

二、三相异步电动机的调速

异步电动机的公式：n = 60f₁(1 - s) / p

1.变频调速

改变 f₁→改变n（无级调速：n可连续调节），当我们采用变频调速时，通常希望电动机的主磁通Φm保持不变。因为增大Φm将引起磁路过分饱和，激磁电流大大增加，功率
因数降低，若Φm太小，则电机容量得不到充分利用。
根据公式：U₁ ≈ E = 4.44 f₁ N₁K _N1Φm，故当U₁ / f₁ = 常数，Φm不变。

2.变极调速（笼型）

• 定子绕组需有特殊的绕法，使绕组的极对数能随外部接线的改变而改变。属于有级调速，具有两种不同转速的电动机称为双速电动机。要想实现极对数的改变，只要改变定子半相绕组的电流方向即可。
• 变极调速一般适用于笼型异步电动机（其转子极对数可自动改变）

3.改变转差率调速

（1）降压调速

（2）转子外串附加电阻调速（绕线型）
转子外串附加电阻会导致转子铜耗增大，输出功率下降，效率也随之降低，机械特性变软，负载变化时转速将发生显著变化。

（3）转子外串附加电动势调速（绕线型）
当转子回路串入与转子电动势 sE₂ 频率相同而相位相反的附加电动势E_f后，转子电流如下所示，其调速范围小，功率因数低，用于大功率绕线异步电动机。

刚串入E_f时，I2↓ → T↓ < TL → n↓ → s↑ → I2↑ → T↑ → 直到 T = T_L → n不变（但已比原来的小）

三、三相异步电动机的制动

（1）能耗制动：切掉定子绕组，同时将其中两相通入直流电源。
其原理是通过定子绕组的直流励磁建立一个恒定磁场，旋转转子和恒定磁场间相互作用，产生制动性电磁转矩，使拖动系统快速停车或使位能性负载匀速下放，制动过程中，大部分动能或势能均消耗在转子回路的电阻上。
（2）反接制动：分为转速反向、两相反接两种方法。
转速反向：通过外部条件令转子反转。
两相反接：通过改变外加三相电源的相序。
对于反抗性负载：将三相电源的两相对调。
●对于位能性负载：重物提升时，电机工作在电动机状态，当重物下降时，由于转速反向，导致机械轴上的输出功率反向，此时电机的运行状态与反抗性负载两相绕组反接情况相同。
●反接制动过程中，电机既从转子轴上输入节选功率，又从电网中吸收电磁功率，这两部分功率都最终通过转子回路电阻消耗掉——转子将严重发热，不能长时间运行在此状态。
（3）回馈制动：异步电动机的转子转速超过同步转速的一种制动状态。
在位能性负载作用下，可以产生回馈制动。（与他励直流拖动情况类似），需要说明的是，回馈制动时电机尽管工作在发电状态，但是仍需从电网吸收滞后无功功率。

四、异步电动机变压调速原理及电路

1.交流调速系统的主要类型

异步电机：现有文献中介绍的异步电机调速方法种类繁多，常见的有：
①降电压调速
②转差离合器调速
③转子串电阻调速
④绕线转子电动机串级调速和双馈电动机调速
⑤变极对数调速
⑥变压变频调速
按照交流异步电机的原理，从定子传入转子的电磁功率 P_m可分成两部分：
P_mech : 拖动负载的有效功率，称作机械功率；P_s：传输给转子电路的转差功率,与转差率s成正比，存在以下关系
P_m = P_mech + P_s ；P_mech = (1 - s) P_m ；P_s = sP_m
从能量转换的角度上看，转差功率是否增大，是消耗掉还是得到回收，是评价调速系统效率高低的标志。从这点出发，可以把异步电机的调速系统分成三类。
（1）转差功率消耗型调速系统
此类型的全部转差功率都转换成热能消耗在转子回路中，上述的第①、②、③三种调速方法都属于这一类。
优点：可是这类系统结构简单，设备成本最低，所以还有一定的应用价值。
缺点：在三类异步电机调速系统中，这类系统的效率最低，而且越到低速时效率越低，它是以增加转差功率的消耗来换取转速的降低的（恒转矩负载时）。

（2）转差功率馈送型调速系统
第④种调速方法属于这一类。
优点：在这类系统中，除转子铜损外，大部分转差功率在转子侧通过变流装置馈出或馈入，转速越低，能馈送的功率越多，无论是馈出还是馈入的转差功率，扣除变流装置本身的损耗后，最终都转化成有用的功率，因此这类系统的效率较高。
缺点：复杂，需要增加一些设备，价格贵。

（3）转差功率不变型调速系统
第⑤、⑥两种调速方法属于此类
优点：转差功率只有转子铜损，而且无论转速高低，转差功率基本不变，因此效率更高，其中变极对数调速是有级的，应用场合有限。只有变压变频调速应用最广，可以构成高动态性能的交流调速系统，取代直流调速；
缺点：但在定子电路中须配备与电动机容量相当的变压变频器，相比之下，设备成本最高。

2.异步电动机的变压调速原理

变压调速：就是通过改变定子外加电压来改变电磁转矩，从而在一定的输出转矩下达到改变电动机转速的目的。
不可逆控制：TVC的变压控制方式：相位控制、周期控制
可逆和制动控制：晶闸管1至6控制电动机正转运行，反转时，可由晶闸管1，4 和 7至10 提供逆相序电源，同时也可用于反接制动。
当需要能耗制动时，例如让 1，2，6 三个器件导通，其余均关断，就可使定子绕组中流过半波直流电流，对旋转着的电动机转子产生制动作用。必要时，还可以在制动电路中串入电阻以限制制动电流。

3.异步电动机改变电压时的机械特性

假定条件：①忽略空间和时间谐波，②忽略磁饱和，③忽略铁损。

可以看出其机械特性中，T_e及T_emax与U_s²成正比 s_m与 U_s无关。
这样，不同电压下的机械特性如下图所示，当带恒转矩负载时，普通笼型异步电机变电
压时的稳定工作点为A，B，C，转差率s 的变化范围不超过0至s_m，调速范围有限。如果带风机类负载运行，则工作点为D，E，F调速范围可以大一些。

★为了能在恒转矩负载下扩大调速范围，并使电机能在较低转速下运行而不致过热，就要求电机转子有较高的电阻值，由此我们引出交流力矩电机的概念。
优点：带恒转矩负载时的变压调速范围增大了，堵转工作也不致烧坏电机，这种电机又称作交流力矩电机。
缺点：机械特性较软。

五、闭环控制的变压调速系统及其静特性

采用普通异步电机的变电压调速时，调速范围很窄，采用高转子电阻的力矩电机可以增大调速范围，但机械特性又变软，因而当负载变化时静差率很大，开环控制很难解决这个矛盾。根据直流电机的经验，既然开环不行，那咱试试闭环，引入转速负反馈。

当系统带负载在A 点运行时，如果负载增大引起转速下降，反馈控制作用能提高定子电压，从而在右边一条机械特性上找到新的工作点 A´ 。同理，当负载降低时，会在左边一条特性上得到定子电压低一些的工作点A"，按照反馈控制规律，将 A´，A，A" 连接起来便是闭环系统的静特性。
●尽管异步电机的开环机械特性和直流电机的开环特性差别很大, 但是在不同电压的开环机械特性上各取一个相应的工作点，连接起来便得到闭环系统静特性，这样的分析方法对两种电机是完全一致的。
●跟直流电机类似，尽管异步力矩电机的机械特性很软，但由系统放大系数决定的闭环系统静特性却可以很硬。如果采用PI调节器，照样可以做到无静差。改变给定信号，则静特性平行地上下移动，达到调速的目的。

★异步电机闭环调压调速系统与直流电机闭环闭环调压调速系统的不同之处
静特性左右两边都有极限，它们分别是是额定电压下和最小输出电压下的机械特性。当负载变化时，如果电压调节到极限值，闭环系统便失去控制能力，系统的工作点只能沿着极限开环特性变化

六、变压控制在软起动器和轻载降压节能运行中的应用

除了调速系统以外，异步电动机变压控制在软起动器和轻载降压节能运行中也得到了广泛的应用。

1.软起动器

异步电动机起动时起动转矩不大，而起动电流很大，将使电压损失过大，起动转矩不够无法起动；绕组发热，绝缘老化，缩短使用寿命；造成过流保护装置误动作、跳闸；影响其他设备的正常运行。所以，电动机起动时，在保证一定大小起动转矩的前提下，还要求限制起动电流在允许的范围内。

小容量电机：只要供电网络和变压器的容量足够大（一般要求比电机容量大4倍以上），而供电线路并不太长（起动电流造成的瞬时电压降落低于10%~15%），可以直接通电起动。如7.5kW以下的电机可直接启动。
中、大容量电动机：其起动电流大，会使电网压降过大，影响其他用电设备的正常运行，甚至使该电动机本身根本起动不起来。这时，必须采取措施来降低其起动电流，常用的办法是降压起动。
（1）降压起动的矛盾：当电压降低时，起动电流将随电压成正比地降低，从而可以避开起动电流冲击的高峰，但是起动转矩与电压的平方成正比，起动转矩的减小将比起动电流的降低更快，降压起动时又会出现起动转矩够不够的问题。因此降压起动只适用于中、大容量电动机空载（或轻载）起动的场合。
（2）软起动方法
控制目的：限制起动电流并保持恒值，直到转速升高后电流自动衰减下来（图中曲线c）。
使用设备：带电流闭环的电子控制软起动器。主电路采用晶闸管交流调压器，用连续地改变其输出电压来保证恒流起动，稳定运行时可用接触器给晶闸管旁路，以免晶闸管不必要地长期工作

起动电流的确定：视起动时所带负载的大小，起动电流可在(0.5至4) I_sN 之间调整，以获得最佳的起动效果。
优点：起动时间也短于一级降压起动。
限制：不宜于满载起动。负载略重或静摩擦转矩较大时，可在起动时突加短时的脉冲电流，以缩短起动时间。

2.轻载降压节能运行

三相异步电动机运行时的总损耗可用下式表达：
∑p = p_Cus + p_Fe + p_Cur + p_mech + p_stray
（p_Cus——定子铜损；p_Fe——铁损；p_Cur——转子铜损；p_mech——机械损耗；p_stray——杂散损耗）
●当电动机在额定工况下运行时，由于输出功率大，总损耗只占很小的成分，所以额定效率 η_N 较高，一般可达75% ~ 95%。电动机在正常运行时，气隙磁通 m 基本不变，因此轻载时转子电流 Ir’很小，P_Cur很小，但铁耗P_Fe，机械损耗P_mech，以及杂散损耗P_stray基本不变。所以效率公式中分母的减小要小于分子，所以整个分数变得更小，效率将急剧降低。如果电动机长期轻载运行，将无谓地消耗许多电能。
●由上述分析可知，为了减少轻载时的能量损耗，关键是降低气隙磁通Φm，这样可以同时降低铁损P_Fe和励磁电流I₀，降低定子电压可以达到此目的。
所以综上两点轻载时要降压运行。

但是，如果过份降低电压和磁通，转子电流Ir’必然增大，则定子电流Is 反而可能增加，铁损的降低将被铜损的增加填补，效率反而更差了。所以降压确实是刚需，但得在降压时采用最佳电压值。

第二章——异步电机变压变频调速系统

异步电机的变压变频调速系统一般简称为变频调速系统。由于在调速时转差功率不随转速而变化，调速范围宽，无论是高速还是低速时效率都较高，在采取一定的技术措施后能实现高动态性能，可与直流调速系统媲美。

一、变压变频调速的基本控制方式

在进行电机调速时，常须考虑的一个重要因素是：希望保持电机中每极磁通量Φm 为额定值不变。对于直流电机，励磁系统是独立的，只要对电枢反应有恰当的补偿，Φm 保持不变是很容易做到的，而在交流异步电机中，磁通Φm 由定子和转子磁势合成产生，要保持磁通恒定就需要费一些周折了。
●异步电机定子每相电动势有效值E_g = 4.44f₁N_sk_NsΦm
E_g——气隙磁通在定子每相中感应电动势的有效值
所以只要控制好 E_g 和 f₁ ，便可达到控制磁通Φm的目的，对此，需要考虑基频（额定频率）以下和基频以上两种情况。
（1）基频以下调速
要保持Φm 不变，当频率f₁ 从额定值f_1N 向下调节时，必须同时降低E_g ，使 E_g / f₁ = 常值，即采用恒值电动势频率比的控制方式。然而，绕组中的感应电动势是难以直接控制的，但是当电动势值较高时，可以忽略定子绕组的漏磁阻抗压降，而认为定子相电压U_s ≈ E_g，则得 U_s / f₁ = 常值，这是恒压频比的控制方式。
但是，在低频时 U_s 和 E_g 都较小，定子阻抗压降所占的份量就比较显著，不再能忽略，这时需要人为地把电压Us 抬高一些，以便近似地补偿定子压降。
在实际应用中，由于负载大小的不同，需要补偿的定子压降值也不一样，在控制软件中，需备有不同斜率的补偿特性，以便用户选择。

（2）基频以上调速
在基频以上调速时，频率应该从f_1N向上升高，定子电压Us却不可能超过额定电压U_sN，最多只能保持Us = U_sN，这将迫使磁通与频率成反比地降低，相当于直流电机弱磁升速的情况。
如果电机在不同转速时所带的负载都能使电流达到额定值，即都能在允许温升下长期运行，则转矩基本上随磁通变化，因为T_e = KΦmI_rcosφ_r
按照电力拖动原理，在基频以下，磁通恒定时转矩也恒定，属于“恒转矩调速”性质，而在基频以上，转速升高时转矩降低，基本上属于“恒功率调速”。

二、异步电动机电压－频率协调控制方式下的机械特性

1.恒压恒频正弦波供电时异步电动机的机械特性

根据一系列的公式变换，当定子电压Us和电源角频率ω1恒定时，可取得其机械特性。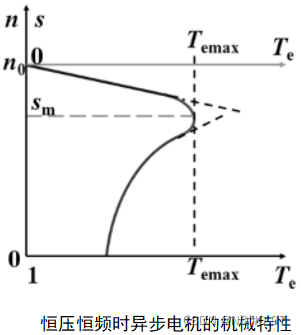

该特性称为自特性（或固有特性）

2.基频以下电压-频率协调控制时的机械特性

（1）恒压频比控制（Us / ω₁ = constant）
当电动势值较高时，可以忽略定子绕组的漏磁阻抗压降，而认为定子相电压U_s ≈ E_g = 4.44f₁N_sk_NsΦm，则得 U_s / f₁ = 常值，气隙磁通 Φm 近似不变。
●当 U_s / f₁ 为恒值时，对于同一转矩Te，sω₁ 是基本不变的，因而 Δn 也是基本不变的。这就是说，在恒压频比的条件下改变频率ω₁时，机械特性基本上是平行下移。
●恒转矩负载下，转差功率与转速无关，故称作**“转差功率不变型”调速方法**。
●与直流调压调速不同的是，当转矩增大到最大值以后，转速再降低，特性就折回来了，而且频率越低时最大转矩值越小。

这时有一个特点，最大转矩T_emax 是随着的 ω₁降低而减小的。频率很低时，T_emax太小将限制电机的带载能力，因此采用定子压降补偿：适当地提高电压Us，可增强带载能力。

（2）恒 E_g / ω₁ 控制（保持气隙磁通恒定）
E_g：气隙（或互感）磁通在定子每相绕组中的感应电动势
E_s：定子全磁通在定子每相绕组中的感应电动势
E_r：转子全磁通在转子绕组中的感应电动势(折合到定子边)
●如果在电压－频率协调控制中，恰当地提高电压Us的数值，使它在克服定子阻抗压降以后，能维持 E_g / ω₁ 为恒值（基频以下），无论频率高低，每极磁通 Φm 均为常值。而这就是补偿电压的目标，就是为了使U_s = E_g 。
●恒压频比Us / ω₁控制与恒E_g / ω₁ 控制的性能比较，见下图。
值得注意的是，当 E_g / ω₁ 为恒值时，T_emax 恒定不变，其稳态性能优于恒Us / ω₁控制的性能。这正是恒 U_s / ω₁ 控制中补偿定子压降所追求的目标。

（3）恒 E_r/ ω₁ 控制（保持转子磁通恒定）
E_r：转子全磁通在转子绕组中的感应电动势(折合到定子边)
此时不必再作任何近似，转矩Te即与转差率s成正比，这时的机械特性完全是一条直线，见上图。
显然，恒 E_r’ / ω₁ 控制的稳态性能最好，可以获得和直流电机一样的线性机械特性。这正是高性能交流变频调速所要求的性能。
转子全磁通的感应电动势 Er 应该对应于 转子全磁通幅值Φrm：E_r = 4.44f₁N_sk_NsΦrm
由此可见，只要能够按照转子全磁通幅值 Φrm = 恒值进行控制，就可以获得恒E_r / ω₁ 了。这正是矢量控制系统所遵循的原则。

（4）几种协调控制方式的比较
综上所述，在正弦波供电时，按不同规律实现电压－频率协调控制可得不同类型的机械特性。
●恒压频比（Us / ω₁ = 恒值 ）控制最容易实现，它的变频机械特性基本上是平行下移，硬度也较好，能够满足一般的调速要求，但低速带载能力有些差强人意，须对定子压降实行补偿。
●恒E_g / ω₁ 控制是通常对恒压频比控制实行电压补偿的标准,可以在稳态时达到Φm = 恒值，从而改善了低速性能。但机械特性还是非线性的，产生转矩的能力仍受到限制。
●恒 E_r / ω₁ 控制可以得到和直流他励电机一样的线性机械特性，按照转子全磁通Φrm恒定进行控制，即得E_r / ω₁ = 恒值，而且，在动态中也尽可能保持Φrm 恒定是矢量控制系统的目标，当然实现起来是比较复杂的。

3.基频以上恒压变频时的机械特性

当角频率提高时，同步转速随之提高，最大转矩减小，机械特性上移，而形状基本不变，如图所示。由于频率提高而电压不变，气隙磁通势必减弱，导致转矩的减小，但转速升高了，可以认为输出功率基本不变。所以基频以上变频调速属于弱磁恒功率调速。

在基频以下，磁通恒定时转矩也恒定，属于“恒转矩调速”性质，而在基频以上，转速升高时转矩降低，基本上属于“恒功率调速”。

以上所分析的机械特性都是在正弦波电压供电下的情况。如果电压源含有谐波，将使机械特性受到扭曲，并增加电机中的损耗。因此在设计变频装置时，应尽量减少输出电压中的谐波。

三、电力电子变压变频器的主要类型

变频器是将固定频率和电压的交流电变换为频率和电压连续可调的交流电的装置。变频器是运动控制系统的功率变换单元和执行部件。

1.交-直-交和交-交变压变频器

（1）交-直-交变压变频器
交-直-交变压变频器先将工频交流电源通过整流器变换成直流，再通过逆变器变换成可控频率和电压的交流。在这类装置中，一般用不可控整流，则输入功率因数不变；用PWM逆变，则输出谐波可以减小。
PWM逆变器需要全控式电力电子器件，其输出谐波减小的程度取决于PWM的开关频率，而开关频率则受器件开关时间的限制。

PWM变压变频器的优点：
●在主电路整流和逆变两个单元中，只有逆变单元可控，通过它同时调节电压和频率，结构简单。采用全控型的功率开关器件，只通过驱动电压脉冲进行控制，电路也简单，效率高。
●输出电压波形虽是一系列的PWM波，但由于采用了恰当的PWM控制技术，正弦基波的比重较大，影响电机运行的低次谐波受到很大的抑制, 因而转矩脉动小, 提高了系统的调速范围和稳态性能。
●逆变器同时实现调压和调频，动态响应不受中间直流环节滤波器参数的影响，系统的动态性能也得以提高。
●采用不可控的二极管整流器，电源侧功率因素较高，且不受逆变输出电压大小的影响。

（2）交-交变压变频器
交-交变压变频器只有一个变换环节，把恒压恒频的交流电源直接变换成VVVF输出，因此又称直接式变压变频器。 有时为了突出其变频功能，也称作周波变换器。
常用的交-交变压变频器输出的每一相都是一个由正、反两组晶闸管可控整流装置反并联的可逆线路, 也就是说，每一相都相当于一套直流可逆调速系统的反并联可逆线路。

●交-交变压变频器的控制方式——整半周控制方式
正、反两组按一定周期相互切换，在负载上就获得交变的输出电压 u₀。u₀的幅值决定于各组可控整流装置的控制角α，u₀的频率决定于正、反两组整流装置的切换频率。如果控制角一直不变，则输出平均电压是方波

●三相交交变频电路可以由3个单相交交变频电路组成，如果每组可控整流装置都用桥式电路，含6个晶闸管（当每一桥臂都是单管时），则三相可逆线路共需36个晶闸管。

交－交变压变频器的特点及用途：
●所用的器件数量多，总体设备相当庞大;
●这些设备都是直流调速系统中常用的可逆整流装置，在技术上和制造工艺上都很成熟。
●输入功率因数较低，谐波电流含量大，频谱复杂，因此须配置谐波滤波和无功补偿设备。
●最高输出频率不超过电网频率的1/2
●主要用途：用于轧机主传动、球磨机、水泥回转窑等大容量、低转速的调速系统，供电给低速电机直接传动时，可以省去庞大的齿轮减速箱。

（3）交-交变频器和交-直交变频器主要特点比较

2.电压源型逆变器和电流源型逆变器

在交-直-交变压变频器中，按照中间直流环节直流电源性质的不同，逆变器可以分成电压源型和电流源型两类，两种类型的实际区别在于直流环节采用怎样的滤波器。
●在交—直—交变压变频装置中，当中间直流环节采用大电容滤波时，直流电压波形比较平直，在理想情况下是一个内阻抗为零的恒压源，输出交流电压是矩形波或阶梯波，这类变频装置叫做电压源型变频器。
●当交—直—交变压变频装置的中间直流环节采用大电感滤波时，直流电流波形比较平直，因而电源内阻抗很大，对负载来说基本上是一个电流源，输出交流电流是矩形波或阶梯波，这类变频装置叫做电流源型变频器。
●电压源型和电流源型逆变器性能比较

3.180º导通型和120º导通型（电压型）逆变器

交-直-交变压变频器中的逆变器一般接成三相桥式电路，以便输出三相交流变频电源，下图为6个电力电子开关器件VT1 ~ VT6 组成的三相逆变器主电路，图中用开关符号代表任何一种电力电子开关器件。
控制各开关器件轮流导通和关断，可使输出端得到三相交流电压。在三相桥式逆变器中，有180°导通型和120°导通型两种换流方式。

（1）180°导通型控制方式
定义：同一桥臂上、下两管之间互相换流的逆变器称作180°导通型逆变器。
由于每隔60°有一个器件开或关，在180°导通型逆变器中，除换流期间外，每一时刻总有3个开关器件同时导通，导通顺序：561-612-123-234-345-456-561

●注意：必须防止同一桥臂的上、下两管同时导通，否则将造成直流电源短路，谓之“直通”。
在换流时，必须采取**“先断后通”的方法，即先给应关断的器件发出关断信号，待其关断后留一定的时间裕量，叫做“死区时间”**，再给应导通的器件发出开通信号。死区时间的长短视器件的开关速度而定，器件的开关速度越快时，所留的死区时间可以越短。
为了安全起见，设置死区时间是非常必要的，但它会造成输出电压波形的畸变。

（2）120°导通型控制方式
定义：换流是在不同桥臂中同一排左、右两管之间进行的。
每个开关器件一次连续导通120°，在同一时刻只有两个器件导通。开关导通顺序：61-12-23-34-45-56-61。如果负载电机绕组是Y联结，则只有两相导电，另一相悬空。

（3）二者对比
●在120°方式中，在同一时刻只有两个器件导通，上下两管之间有60°的间隙，对换流的安全有利，但是管子的利用率较低，并且若电机采用星形接法，则始终有一相绕组断开，在换流时会引起较高的感应电势，应采取过电压保护措施。
●而180°导通方式在同一时刻有三个器件导通，无论电动机在三角形还是星形接法时，正常工作都不会产生过电压，因此对于电压型逆变器，180°导通方式应用较为普遍。

四、变压变频调速系统中的脉宽调制(PWM)技术

左边是不可控整流桥，将三相交流电整流成电压恒定的直流电压。中间滤波环节是为了减小直流电压脉动而设置的。右边是逆变器，将直流电压变换为频率与电压均可调的交流电。

1.正弦波脉宽调制(SPWM)技术

（1）SPWM调制原理：按照波形面积相等的原则，每一个矩形波的面积与相应位置的正弦波面积相等，因而这个序列的矩形波与期望的正弦波等效。

（2）SPWM调制方法：以正弦波作为逆变器输出的期望波形，以频率比期望波高得多的等腰三角波作为载波，并用频率和期望波相同的正弦波作为调制波。用调制波与载波相交的交点确定逆变器开关器件的通断时刻，从而获得在正弦调制波的半个周期内呈两边窄中间宽的一系列等幅不等宽的矩形波。

（3）SPWM控制方式：
●单极性控制方式：如果在正弦调制波的半个周期内，三角载波只在正或负的一种极性范围内变化，所得到的SPWM波也只处于一个极性的范围内，叫做单极性控制方式。
●双极性控制方式：如果在正弦调制波半个周期内，三角载波在正负极性之间连续变化，则SPWM波也是在正负之间变化，叫做双极性控制方式。

（4）控制电路采样方法介绍：
●自然采样法：是按照正弦波和三角波的实际交点进行脉冲宽度和间隙时间的实时计算获得开关管的导通时间和导通间隙,从而生成SPWM波形。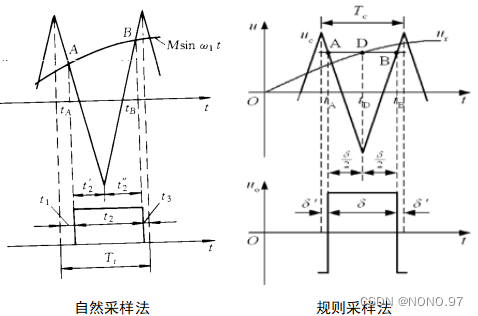

●规则采样法：三角波两个正峰值之间为一个采样周期T_c，自然采样法中，脉冲中点不和三角波一周期的中点（即负峰点）重合，规则采样法使两者重合，每个脉冲的中点都以相应的三角波中点为对称，使计算大为简化。
★在三角波的负峰时刻t_D对正弦信号波采样得D点，过 D作水平直线和三角波分别交于A、B点，在A点时刻 t_A和B点时刻 t_B控制开关器件的通断。脉冲宽度δ 和 用自然采样法得到的脉冲宽度非常接近。

2.电流滞环跟踪PWM(CHBPWM)控制技术

应用PWM控制技术的变压变频器一般都是电压源型的，它可以按需要方便地控制其输出电压，为此前面的SPWM控制技术都是以输出电压近似正弦波为目标的，但是，在交电流电机中，实际需要保证的应该是正弦波电流，因为在交流电机绕组中只有通入三相平衡的正弦电流才能使合成的电磁转矩为恒定值，不含脉动分量。因此，若能对电流实行闭环控制，以保证其正弦波形，显然将比电压开环控制能够获得更好的性能。由此我们引入电流滞环跟踪PWM控制技术。
（1）电流滞环跟踪控制的原理
图中，电流控制器是带滞环的比较器HBC，环宽为2h。将给定电流 i*_a 与输出电流 i_a进行比较，电流偏差 Δi_a超过时 ±h，经滞环控制器HBC控制逆变器 A相上（或下）桥臂的功率器件动作。

（2）在i*_a的正半周，VT1与VD4交替工作。
●如果 Δi_a = i_a - i_a，滞环控制器HBC输出正电平，驱动VT1导通, 变压变频器输出正电压，使 i_a增大。
●当增长到与 i*_a相等时*，虽然 Δi_a = 0，但HBC仍保持正电平输出，保持导通，使i_a继续增大。
●直到达到 i_a = i*_a + h ，Δi_a = –h ，使滞环翻转，HBC输出负电平，关断VT1，并经延时保护后驱动VT4。但此时VT4未必能够导通，由於电机绕组的电感作用，电流i
a不会反向，而是通过二极管VD4续流，使VT4受到反向钳位而不能导通。
●此后，i_a逐渐减小，直到 i_a = i*_a + h时，到达滞环偏差的下限值，使HBC再翻转，又重复使VT1导通。
这样，VT1与VD4交替工作，使输出电流给定值之间的偏差保持在范围内，在正弦波上下作锯齿状变化。从图中可以看到, 输出电流是十分接近正弦波的。可以看出，在半个周期内围绕正弦波作脉动变化，不论在的上升段还是下降段，它都是指数曲线中的一小部分，其变化率与电路参数和电机的反电动势有关。

（3）CHBPWM的特点
●优点：精度高、响应快，且易于实现。
●不足：但功率开关器件的开关频率不定，电流跟踪控制的精度与滞环的环宽有关，同时还受到功率开关器件允许开关频率的制约。

当环宽选得较大时，可降低开关频率，但电流波形失真较多，谐波分量高；如果环宽太小，电流波形虽然较好，却使开关频率增大了。所以在实用中，应在充分利用器件开关频率的前提下，正确地选择尽可能小的环宽。

3.电压空间矢量PWM(SVPWM)控制技术(或称磁链跟踪控制技术)

经典的SPWM控制主要着眼于使变压变频器的输出电压尽量接近正弦波，并未顾及输出电流的波形。而电流滞环跟踪控制则直接控制输出电流，使之在正弦波附近变化，这就比只要求正弦电压前进了一步。然而交流电动机需要输入三相正弦电流的最终目的是在电动机空间形成圆形旋转磁场，从而产生恒定的电磁转矩。如果对准这一目标，把逆变器和交流电动机视为一体，按照跟踪圆形旋转磁场来控制逆变器的工作，其效果应该更好。这种控制方法称作“磁链跟踪控制”。
（1）空间矢量的定义
交流电动机绕组的电压、电流、磁链等物理量都是随时间变化的，分析时常用时间相量来表示。如果考虑到它们所在绕组的空间位置，也可以定义为空间矢量u_A0，u_B0，u_C0。空间矢量u_A0，u_B0，u_C0的方向始终处于各相绕组的轴线上，而大小则随时间按正弦规律脉动，时间相位互相错开的角度也是120°。

合成空间矢量u_s ：与电机原理中三相脉动磁动势相加后产生旋转磁动势相仿，由三相定子电压空间矢量相加合成的空间矢量u_s 是一个旋转的空间矢量，它的幅值不变，是每相电压值的 3 / 2 倍。
u_s = 1.5U_me^jωt = U_se^jωt
当电源频率不变时，合成空间矢量 u_s 以电源角频率 ω₁ 为电气角速度作恒速旋转。当某一相电压为最大值时，合成电压矢量 u_s 就落在该相的轴线上。

（2）电压与磁链空间矢量的关系
三相对称定子绕组由三相平衡电压供电时，每一相都可以写出一个电压平衡方程式。将这三相的电压平衡方程式相加，即得用合成空间矢量表示的定子电压方程式为 u_s = R_si_s + dΨ_s / dt，当电动机转速不是很低时，定子电阻压降在式（6-40）中所占
的成分很小，可忽略不计，则定子合成电压与合成磁链空间矢量的近似关系为 u_s = dΨ_s / dt，或 Ψ_s = ∫ u_sdt + Ψ_s(0)
●磁链运动轨迹：当电动机由三相平衡正弦电压供电时，电动机定子磁链幅值恒定，其空间矢量Ψs以恒速旋转，磁链矢量顶端的运动轨迹呈圆形（一般简称为磁链圆），即 Ψ_s = Ψ_me^jωt。
联立上式，得 u_s ≈ jωΨ_me^jωt = ωΨ_me^j(ωt + π/2)^，上式表明，当磁链幅值一定时，u_s的大小与ω（或供电电压频率f1）成正比，其方向则与磁链矢量正交，即磁链圆的切线方向。
●磁场轨迹与电压空间矢量运动轨迹的关系：如下图所示，当磁链矢量Ψ_s在空间旋转一周时，电压矢量 u_s 也连续地按磁链圆的切线方向运动2π弧度，其轨迹与磁链圆重合。这样，电动机旋转磁场的轨迹问题就可转化为电压空间矢量的运动轨迹问题。

（3）六拍阶梯波逆变器与正六边形空间旋转磁场
逆变器采用上、下管换流(180°导通型)，功率开关器件共有8种工作状态（见上表述），其中6种有效开关状态: 612，123，234，345，456，561。上桥臂开关导通用“1”表示，上桥臂开关关断用“0”表示。

以上以两个电压矢量为例，这样，在一个周期中6 个电压空间矢量共转过2π弧度，形成一个封闭的正六边形，如图所示。如前所述，这样一个由电压空间矢量运动所形成的正六边形轨迹也可以看作是异步电动机定子磁链矢量端点的运动轨迹。

需注意几点：
●磁链矢量的增量大小与其上作用的电压矢量大小成正比，方向与其方向一致。
●在任何时刻，所产生的磁链增量的方向决定于所施加的电压矢量的方向，其幅值则正比于施加电压矢量的幅值及作用时间。

4.电压空间矢量的线性组合与SVPWM控制

如果交流电动机仅由常规的六拍阶梯波逆变器供电，磁链轨迹便是六边形的旋转磁场，这显然不象在正弦波供电时所产生的圆形旋转磁场那样能使电动机获得匀速运行，而且将导致转矩和转速脉动。如果想获得更多边形或逼近圆形的旋转磁场，就必须在每一个π/3期间内出现多个工作状态，以形成更多的相位不同的电压空间矢量。为此，采用SVPWM控制对逆变器的控制模式进行改造，以使旋转磁链轨迹的逼近圆形。为此引出一个圆形旋转磁场逼近方法——线性组合法。
①基本思路
如果要逼近圆形，可以增加切换次数，假如磁链增量ΔΨ₁由图中的ΔΨ₁₁，ΔΨ₁₂，ΔΨ₁₃，ΔΨ₁₄这4段组成。这时，每段施加的电压空间矢量的相位都不一样，可以用基本电压矢量线性组合的方法获得。
②线性组合的方法
如图：由电压空间矢量和的线性组合构成新的电压矢量。设在一段换相周期时间T₀中,可以用两个矢量之和表示由两个矢量线性组合后的电压矢量u_s，新矢量的相位为θ。

线性组合公式：ΔΨ_i = u_iΔt，u_i = U_d，u₂ = U_de^jπ/3，u_s = t₁u₁ / T₀ + t₂u₂ / T₀ = u_scosθ + ju_ssinθ

④零矢量的使用：当零矢量作用时，定子磁链矢量的增量ΔΨ_s = 0，表明定子磁链矢量停留不动。
换相周期 T₀ 应由旋转磁场所需的频率决定，当零矢量的引入时 T₀ 与 t1+ t2 未必相等，其间隙时间可用零矢量 u7 或 u8来填补。为了减少功率器件的开关次数，一般使u7 和 u8 各占一半时间，因此 t₇ = t₈ = 0.5（T₀ - t₁ - t₂）≥ 0，Δt = NT₀ = π / 3ω₁
⑤电压空间矢量的扇区划分
为了讨论方便起见，可把逆变器的一个工作周期用6个电压空间矢量划分成6个区域，称为扇区，如图所示的Ⅰ, Ⅱ, … , Ⅵ，每个扇区对应的时间均为 π / 3 。由于逆变器在各扇区的工作状态都是对称的，分析一个扇区的方法可以推广到其他扇区。
在常规六拍逆变器中一个扇区仅包含两个开关工作状态。实现SVPWM控制就是要把每一扇区再分成N个对应时间为T0 的小区间。按照上述方法插入若干个线性组合的新电压空间矢量u_s，以获得优于正六边形的多边形（逼近圆形）旋转磁场。
T₀ = Δt / N = π / 3ω₁N

⑥按最小开关损耗原则确定开关状态的顺序
在实际系统中，不同开关状态的顺序必须遵守下述原则：每次切换开关状态时，只切换一个功率开关器件，以满足最小开关损耗。尽量使PWM输出波型对称，以减少谐波分量。

一个扇区内所分的小区间越多，就越能逼近圆形旋转磁场。实际的定子磁链矢量轨迹在期望的磁链圆周围波动。N越大，磁链轨迹越接近于圆，但开关频率随之增大。由于N是有限的，所以磁链轨迹只能接近于圆，而不可能等于圆。

★小结——SVPWM控制模式有以下特点：
●逆变器的一个工作周期分成6个扇区，每个扇区相当于常规六拍逆变器的一拍。为了使电动机旋转磁场逼近圆形，每个扇区再分成若干个小区间 T0 ， T0 越短，旋转磁场越接近圆形，但 T0 的缩短受到功率开关器件允许开关频率的制约。
●在每个小区扇间内虽有多次开关状态的切换，但每次切换都只涉及一个功率开关器件，因而开关损耗较小。
●每个小扇区间均以零电压矢量开始，又以零矢量结束。
●利用电压空间矢量直接生成三相PWM波，计算简便。
●采用SVPWM控制时，逆变器输出线电压基波最大值为直流侧电压，这比一般的SPWM逆变器输出电压提高了15%。

五、基于异步电动机稳态模型的变压变频调速

风机和水泵等负载，并不需要很高的动态性能，只要在一定范围内能实现高效率的调速就行，因此可以只根据电机的稳态模型来设计其控制系统。依据前述异步电机的稳态数学模型来实现电压-频率协调控制，可以采用转速开环恒压频比带低频电压补偿的控制方案，这就是常用的通用变频器控制系统。如果要求更高一些的调速范围和起制动性能，可以采用转速闭环转差频率控制的方案。

1.一种典型的数字控制通用变频器

●主电路——由二极管整流器UR、PWM逆变器UI和中间直流电路三部分组成，一般都是电压源型的，采用大电容C滤波，同时兼有无功功率交换的作用。
●限流电阻——为了避免大电容C在通电瞬间产生过大的充电电流，在整流器和滤波电容间的直流回路上串入限流电阻（或电抗），通上电源时，先限制充电电流，再延时用开关K将短路，以免长期接入时影响变频器的正常工作，并产生附加损耗。
●泵升电压——由于二极管整流器不能为异步电机的再生制动提供反向电流的通路，所以除特殊情况外，通用变频器一般都用电阻吸收制动能量。当电动机减速停车时，驱动信号被封锁，VT1～VT6截止。电动机轴上的机械能要可逆转换为电能，负载发出来的电能会通过VD1～VD6续流管组成的三相整流器向直流侧滤波电容C供电，造成直流母线电压的瞬间急剧升高，这个电压叫泵升电压。其危害是将整流器件瞬间击穿。
●泵升限制电路：当泵升电压升高到一定的限制值时，通过泵升限制电路使开关器件VTb导通，将电机释放的动能消耗在制动电阻上。为了便于散热，制动电阻器常作为附件单独装在变频器机箱外边。
●进线电抗器——二极管整流器虽然是全波整流装置，但由于其输出端有滤波电容存在，因此输入电流呈脉冲波形。为了抑制谐波电流，对于容量较大的PWM变频器，都
应在输入端设有进线电抗器，有时也可以在整流器和电容器之间串接直流电抗器。还可用来抑制电源电压不平衡对变频器的影响。
●检测与保护电路——各种故障的保护由电压、电流、温度等检测信号经信号处理电路进行分压、光电隔离、滤波、放大等综合处理，再进入A/D转换器，输入给CPU作为控制算法的依据，或者作为开关电平产生保护信号和显示信号
●U / f设定——由于通用变频器-异步电动机系统是转速或频率开环、恒压频比控制系统，低频时，或负载的性质和大小不同时，都得靠改变 U / f 函数发生器的特性来补偿，使系统达到 Eg / f₁ 恒定，在通用产品中称作“电压补偿”或“转矩补偿”。
实现补偿的方法有两种：
• 一种是在微机中存储多条不同斜率和折线段的U / f 函数，根据用户需要选择最佳特性；
• 另一种办法是采用霍耳电流传感器检测定子电流或直流回路电流，按电流大小自动补偿定子电压。但无论如何都存在过补偿或欠补偿的可能，这是开环控制系统的不足之处。

●给定积分——由于系统本身没有自动限制起制动电流的作用，因此，频定设定信号必须通过给定积分算法产生平缓升速或降速信号，升速和降速的积分时间可以根据负载需要由操作人员分别选择。

2.转速闭环转差频率控制的变压变频调速系统

任何电力拖动自动控制系统都服从于基本运动方程式：T_e - T_L = Jdω / dt，提高调速系统动态性能主要依靠控制转速的变化率 dω / dt ，根据基本运动方程式，控制电磁转矩Te就能控制dω / dt，因此，归根结底，调速系统的动态性能就是控制转矩的能力。因此，怎样能够通过控制电压（电流）和频率来控制电磁转矩，这是寻求提高动态性能时需要解决的问题。
（1）转差频率控制的基本概念
直流电机的转矩与电枢电流成正比，控制电流就能控制转矩，因此，把直流双闭环调速系统转速调节器的输出信号当作电流给定信号，也就是转矩给定信号。而在交流异步电机中，影响转矩的因素较多，控制异步电动机的问题也就比较复杂。

当电机稳态运行时，s 值很小，因而 ω_s也很小，T_e ≈ K_mΦ_m²ω_s / R’_r，表明，在s 值很小的稳态运行范围内，如果能够保持气隙磁通Φm不变，异步电机的转矩就近似与转差角频率 ω_s 成正比。
这就是说，在异步电机中控制 ω_s ，就和直流电机中控制电流一样，能够达到间接控制转矩的目的。控制转差频率就代表控制转矩，这就是转差频率控制的基本概念，是转差频率控制的基本规律之一。

（2）前提条件：上述规律是在保持Φm恒定的前提下才成立的，于是问题又转化为，如何能保持Φm 恒定？我们知道，按恒 E_g / ω₁ 控制时可保持Φm恒定。由此可见，要实现恒 E_g / ω₁ 控制，须在Us / ω₁ = 恒值的基础上再提高电压Us 以补偿定子电流压降。

上述关系表明，只要 Us和ω₁及 I_s 的关系符合左图所示特性，就能保持恒 E_g / ω₁ 控制，也就是保持 Φm 恒定。这是转差频率控制的基本规律之二。

（3）转差频率控制的规律是：
●在 ω_s ≤ ω_sm的范围内，转矩Te 基本上与ω_s成正比, 条件是气隙磁通不变。
●在不同的定子电流值时, 按上图的函数关系: Us = f (ω₁ , I_s) 去控制定子电压和频率，就能保持气隙磁通Φm恒定。

（4）转差频率控制的变压变频调速系统

控制原理：
频率控制——转速调节器ASR的输出信号是转差频率给定 ω*_s，与实测转速信号ω相加，即得定子频率给定信号ω*₁
即：ω*_s + ω = ω*₁
电压控制——由ω₁和定子电流反馈信号 I_s 从微机存储的 Us = f(ω₁，I_s) 函数中查得定子电压给定信号 U_s* ，用U_s* 和 ω₁* 控制PWM电压型逆变器，即得异步电机调速所需的变压变频电源。

（5）性能评价：
●转差角频率ω*_s与实测转速信号ω相加后得到定子频率输入信号ω*₁这一关系是转差频率控制系统突出的特点或优点。
它表明，在调速过程中，实际频率ω₁随着实际转速ω同步地上升或下降，有如水涨而船高，因此加、减速平滑而且稳定。
●同时，由于在动态过程中转速调节器ASR饱和，系统能用对应于ω_sm的限幅转矩T_em 进行控制，保证了在允许条件下的快速性。
●由此可见，转速闭环转差频率控制的交流变压变频调速系统能够像直流电机双闭环控制系统那样具有较好的静、动态性能，是一个比较优越的控制策略，结构也不算复杂。

★然而它的静、动态性能还不能完全达到直流双闭环系统的水平，存在差距的原因有以下几个方面：
●在分析转差频率控制规律时，是从异步电机稳态等效电路和稳态转矩公式出发的，所谓的“保持磁通Φm恒定”的结论也只在稳态情况下才能成立。在动态中Φm如何变化还没有深入研究，但肯定不会恒定，这不得不影响系统的实际动态性能。
●Us = f(ω₁，I_s) 函数关系中只抓住了定子电流的幅值，没有控制到电流的相位，而在动态中电流的相位也是影响转矩变化的因素。
●在频率控制环节中，取ω₁ = ω_s + ω ，使频率得以与转速同步升降，这本是转差频率控制的优点。然而，如果转速检测信号不准确或存在干扰，也就会直接给频率造成误差，因为所有这些偏差和干扰都以正反馈的形式毫无衰减地传递到频率控制信号上来了。

六、异步电动机的动态数学模型和坐标变换

1.异步电动机动态数学模型的性质

电磁耦合是机电能量转换的必要条件，电流与磁通的乘积产生转矩，转速与磁通的乘积得到感应电动势。无论是直流电动机，还是交流电动机均如此。但是交、直流电动机结构和工作原理的不同，其表达式差异很大。
他励式直流电动机的励磁绕组和电枢绕组相互独立，励磁电流和电枢电流单独可控，励磁和电枢绕组各自产生的磁动势在空间无交叉耦合。气隙磁通由励磁绕组单独产生，而电磁转矩正比于磁通与电枢电流的乘积。保持励磁电流恒定，只通过电枢电流来控制电磁转矩。因此它的动态数学模型只是一个单输入和单输出系统。

交流电机数学模型的性质：
●多变量、强耦合的模型结构
输入变量：异步电机变压变频调速时需要进行电压（或电流）和频率的协调控制，有电压（电流）和频率两种独立的输入变量。
输出变量：除转速外，磁通也得算一个独立的输出变量。因为电机只有一个三相输入电源，磁通的建立和转速的变化是同时进行的，为了获得良好的动态性能，也希望对磁通施加某种控制，使它在动态过程中尽量保持恒定，才能产生较大的动态转矩。
由于这些原因，异步电机是一个多变量（多输入、多输出）系统，而电压（电流）、频率、磁通、转速之间又互相都有影响，所以是强耦合的多变量系统。
●模型的非线性：在异步电动机无法单独对磁通进行控制，电流乘磁通产生转矩，转速乘磁通产生感应电动势，在数学模型中含有两个变量的乘积项。
●模型的高阶性：在三相异步电机定子有三个绕组，转子也可等效为三个绕组，每个绕组产生磁通时都有自己的电磁惯性，再算上运动系统的机电惯性，和转速与转角的积分关系，即使不考虑变频装置的滞后因素，也是一个八阶系统。

总起来说，异步电机的动态数学模型是一个高阶、非线性、多变量、强耦合的系统。

2.三相异步电动机的多变量非线性数学模型

在研究异步电动机的多变量非线性数学模型时，常作如下假设：忽略空间谐波，设三相绕组对称，在空间互差120°电角度，所产生的磁动势沿气隙周围按正弦规律分布；忽略磁路饱和，各绕组的自感和互感都是恒定的；忽略铁心损耗；不考虑频率变化和温度变化对绕组电阻的影响。
无论电机转子是绕线型还是笼型的，都将它等效成三相绕线转子，并折算到定子侧，折算后的定子和转子绕组匝数都相等这样，实际电机绕组就等效成如下图所示的三相异步电机的物理模型。

这时，异步电机的数学模型由:电压方程、磁链方程、转矩方程和运动方程组成。其中磁链方程和转矩方程为代数方程，电压方程和运动方程为微分方程
uA, uB, uC, ua, ub, uc ——定子和转子相电压的瞬时值；
iA, iB, iC, ia, ib, ic ——定子和转子相电流的瞬时值；
ΨA, ΨB, ΨC, Ψa, Ψb, Ψc ——各相绕组的全磁链；
（1）电压方程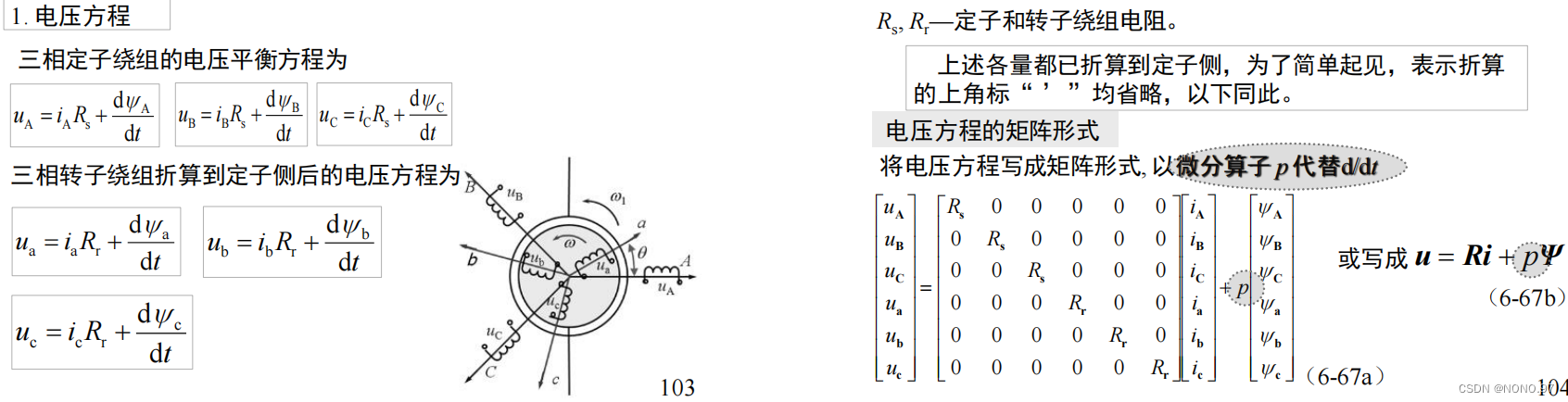

（2）磁链方程
每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和，因此，六个绕组的磁链可表达为下式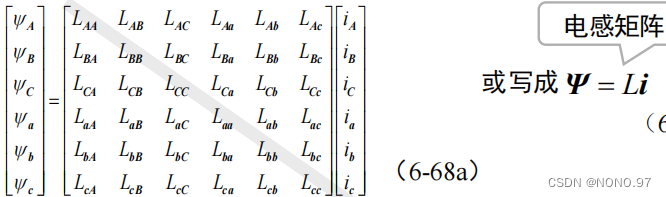

式中，L是6×6电感矩阵，其中对角线元素L_AA，L_BB，L_CC，L_aa，L_bb，L_cc是各有关绕组的自感，其余各项则是绕组间的互感。实际上，与电机绕组交链的磁通主要只有两类：一类是穿过气隙的相间互感磁通，另一类是只与一相绕组交链而不穿过气隙的漏磁通，前者是主要的。

●电感的种类和计算
•定子漏感L_ls ——定子各相漏磁通所对应的电感，由于绕组的对称性，各相漏感值均相等；
•转子漏感L_lr ——转子各相漏磁通所对应的电感。
•定子互感L_ms——与定子一相绕组交链的最大互感磁通
•转子互感L_mr——与转子一相绕组交链的最大互感磁通。
由于折算后定、转子绕组匝数相等，且各绕组间互感磁通都通过气隙，磁阻相同，故可认为 L_ms = L_mr

●自感表达式：对于每一相绕组来说，它所交链的磁通是互感磁通与漏感磁通之和，因此，定子各相自感为L_AA = L_BB = L_CC = L_ms = L_ls，转子各相自感为L_aa = L_bb = L_cc = L_mr + L_lr = L_ms + L_lr，两相绕组之间只有互感。

●互感表达式：
①第一类固定位置绕组的互感：定子三相彼此之间和转子三相彼此之间位置都是固定的，故互感为常值；
三相绕组轴线彼此在空间的相位差是±120°，在假定气隙磁通为正弦分布的条件下，互感值应为L_mscos120° = L_mscos(-120°) = -0.5L_ms于是L_AB = L_BC = L_CA = L_BA = L_CB = L_AC = -0.5L_ms， L_ab = L_bc = L_ca = L_ba = L_cb = L_ac = -0.5L_mr = -0.5L_ms
②第二类变化位置绕组的互感：定子任一相与转子任一相之间的位置是变化的，互感是角位移θ的函数。
定、转子绕组间的互感，由于相互间位置的变化可分别表示为L_Aa = L_Bb = L_Cc = L_aA = L_bB = L_cC = L_mscosθ，L_Ac = L_Ba = L_Cb = L_cA = L_aB = L_bC = L_mscos(θ - 120°)，L_Ab = L_Bc = L_Ca = L_bA = L_cB = L_aC = L_mscos(θ + 120°)。
当定、转子两相绕组轴线一致时，两者之间的互感值最大，就是每相最大互感 L_ms 。

（3）磁链方程



应该指出，上述公式是在线性磁路、磁动势在空间按正弦分布的假定条件下得出来的，但对定、转子电流对时间的波形未作任何假定，式中的i 都是瞬时值。因此，上述电磁转矩公式完全适用于变压变频器供电的含有电流谐波的三相异步电机调速系统。

（4）电力拖动系统运动方程：若忽略电力拖动系统传动机构中的粘性摩擦和扭转弹性，则系统的运动方程式是 T_e - T_L = Jdω / n_pdt，ω = dθ / dt

（5）三相异步电机的数学模型：将上述5个公式综合起来，便构成在恒转矩负载下三相异步电机的多变量非线性数学模型。

异步电动机三相原始模型的性质：
●非线性强耦合性：非线性耦合体现在电压方程、磁链方程与转矩方程。既存在定子和转子间的耦合，也存在三相绕组间的交叉耦合。
●非线性变参数：旋转电动势和电磁转矩中都包含变量之间的乘积，这是非线性的基本因素。定转子间的相对运动，导致其夹角q不断变化，使得互感矩阵为非线性变参数矩阵。

3.坐标变换和变换矩阵

上节中虽已推导出异步电机的动态数学模型，但是，要分析和求解这组非线性方程显然是十分困难的。在实际应用中必须设法予以简化，简化的基本方法是坐标变换。
（1）直流电机的物理模型：直流电机的数学模型比较简单，先分析一下直流电机的磁链关系。

虽然电枢本身是旋转的，但其绕组通过换向器电刷接到端接板上，电刷将闭合的电枢绕组分成两条支路。当一条支路中的导线经过正电刷归入另一条支路中时，在负电刷下又有一根导线补回来。这样电刷两侧每条支路中导线的电流方向总是相同的，因此，电枢磁动势的轴线始终被电刷限定在q 轴位置上，其效果好像一个在q 轴上静止的绕组一样。但电枢绕组实际上是旋转的，会切割d 轴的磁通而产生旋转电动势，这又和真正静止的绕组不同。通常把这种等效的静止绕组称作“伪静止绕组”。
●电枢磁动势的作用可以用补偿绕组磁动势抵消,或者由于其作用方向与 d 轴垂直而对主磁通影响甚微。
●所以直流电机的主磁通基本上唯一地由励磁绕组的励磁电流决定，这是直流电机的数学模型及其控制系统比较简单的根本原因。

（2） 坐标变换的基本思路
从上节分析异步电机数学模型的过程中可以看出，这个数学模型之所以复杂，关键是因为有一个复杂的6X6 电感矩阵，它体现了影响磁链和受磁链影响的复杂关系。因此，要简化数学模型，须从简化磁链关系入手。

交流电机物理模型的等效变换：如果能将交流电机的物理模型等效地变换成类似直流电机的模式，分析和控制就可以大大简化。而坐标变化恰恰是按照这条思路进行的。在这里，不同电机模型彼此等效的原则是：在不同坐标下所产生的磁动势完全一致。
在交流电动机三相对称的静止绕组A,B,C中，通以三相平衡的正弦电流，所产生的合成磁动势是旋转磁动势F，它在空间呈正弦分布，以同步转速（即电流的角频率）顺着A-B-C的相序旋转。根据数学定理，任意对称的多相绕组，通入平衡的多相电流，都能产生旋转磁动势，当然以两相最为简单。所以，三相绕组可以用相互独立的两相正交对称绕组等效代替，等效的原则是产生的磁动势相等。
★注：独立是指两相绕组间无约束条件。对称是指两相绕组的匝数和阻值相等。正交是指两相绕组在空间互差90°

●图b中绘出了两相静止绕组 α和β ，它们在空间互差90°，通以时间上互差90°的两相平衡交流电流，也产生旋转磁动势F 。当图a和b的两个旋转磁动势大小和转速都相等时，即认为图b的两相绕组与图a的三相绕组等效。再看图c中的两个匝数相等且互相垂直的绕组 M 和 T，其中分别通以直流电流 i_m 和 i_t，产生合成磁动势F ，其位置相对于绕组来说
是固定的。
●如果让包含两个绕组在内的整个铁心以同步转速旋转，则磁动势 F 自然也随之旋转起来，成为旋转磁动势。把这个旋转磁动势的大小和转速也控制成与图 a 和图 b 中的磁动势一样，那么这套旋转的直流绕组也就和前面两套固定的交流绕组都等效了。
●当观察者也站到铁心上和绕组一起旋转时，在他看来，M和T 是两个通以直流而相互垂直的静止绕组。
如果控制磁通的位置在M 轴上，就和直流电机物理模型没有本质上的区别了。这时绕组M相当于励磁绕组，T 相当于伪静止的电枢绕组。

由此可见，以产生同样的旋转磁动势为准则，图a的三相交流绕组、图b的两相交流绕组和图c中整体旋转的直流绕组彼此等效。或者说，在三相坐标系下的 i_A、i_B 、i_C，在两相坐标系下的 i_α、i_β和在旋转两相坐标系下的直流i_m、i_t 是等效的，它们能产生相同的旋转磁动势。
有意思的是：就图c 的 M、T 两个绕组而言，当观察者站在地面看上去，它们是与三相交流绕组等效的旋转直流绕组；如果跳到旋转着的铁心上看，它们就的的确确是一个直流电机模型了。这样，通过坐标系的变换，可以找到与交流三相绕组等效的直流电机模型。

（3）三相-两相变换（3/2变换）
现在先考虑上述的第一种坐标变换—— 在三相静止绕组A、B、C和两相静止绕组α、β 之间的变换，或称三相静止坐标系和两相静止坐标系间的变换，简称3/2 变换。


（4）两相静止—两相旋转变换（2s/2r变换）
从图 b的等效两相交流电机绕组到图c的旋转直流电机绕组的物理模型变换，即从两相静止α，β坐标系到两相旋转坐标系M、T变换称作两相—两相旋转变换，简称 2s / 2r 变换，其中 s 表示静止，r 表示旋转。 把两个坐标系画在一起，即得下图。

图中，两相交流电流 i_α、i_β和两个直流电流 i_m、i_t产生同样的以同步转速ω₁旋转的合成磁动势Fs。
●由于各绕组匝数都相等，可以消去磁动势中的匝数，直接用电流表示，例如Fs可以直接标成 i_s 。但必须注意，这里的电流都是空间矢量，而不是时间相量。
●M，T 轴和矢量F_s( i_s)都以转速ω₁旋转，分量 i_m、i_t的长短不变，相当于M，T绕组的直流磁动势。
●但 α、β 轴是静止的，α轴与M 轴的夹角φ 随时间而变化，因此 i_s 在 α、β 轴上的分量的长短也随时间变化，相当于绕组交流磁动势的瞬时值。

4.三相异步电动机在两相坐标系上的数学模型

前面介绍的仅只是数学模型方面的代数变换，没有涉及到电压、磁链等基本方程。
要把三相静止坐标系上的电压方程，磁链方程和转矩方程都变换到两相旋转坐标系上来，可以先利用3/2 变换将方程式中定子和转子的电压、电流、磁链和转矩都变换到两相静止坐标系α、β上，然后再用旋转变换阵C_2s/2r 将这些变量变换到两相旋转坐标系dq 上。
具体的变换运算比较复杂，此处从略，这里直接给出结果。
（1）磁链方程

L_s = 1.5L_ms + L_ls = L_m + L_ls，dq坐标系定子等效两相绕组的自感（定子）
L_r = 1.5L_ms + L_lr = L_m + L_lr，dq坐标系转子等效两相绕组的自感（转子）
两相绕组互感L_m是原三相绕组中任意两相间最大互感（当轴线重合时）的1.5倍，这是因为用两相绕组等效地取代了三相绕组的缘故。由异步电机变换到dq坐标系上的物理模型可见，定子和转子的等效绕组都落在同样的两根轴d和q上，而且两轴互相垂直，它们之间
没有耦合关系。互感磁链只在同轴绕组间存在，所以式中每个磁链分量只剩下两项，电感矩阵比ABC坐标系的6X6 矩阵简单多了。

七、基于动态模型按转子磁链定向的矢量控制系统

前述表明，异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统，通过坐标变换可以使之降阶并化简，但其非线性、多变量的本质并没有改变。需要高动态性能的异步电机调速系统必须在其动态模型的基础上进行分析和设计，但要完成这一任务并非易事。

1.矢量控制系统的基本思路

上节已经叙述，以产生同样的旋转磁动势为准则，在三相坐标系上的定子交流电流 iA、 iB 、iC ，通过三相/两相变换可以等效成两相静止坐标系上的交流电流i_α、i_β ，再通过同步旋转变换，可以等效成同步旋转坐标系上的直流电流i_m 和 i_t 。
把上述等效关系用结构图的形式画出来，如下图所示。从整体上看，输入为A，B，C三相电压，输出为转速ω ，是一台异步电机。从内部看，经过3/2变换和同步旋转变换，变成一台由i_m 和 i_t输入，由ω输出的直流电机。

按转子磁链定向矢量控制的基本思想：
●通过坐标变换，在按转子磁链定向同步旋转正交坐标系中，得到等效的直流电动机模型。
●仿照直流电动机的控制方法控制电磁转矩与磁链，然后将转子磁链定向坐标系中的控制量反变换得到三相坐标系的对应量，以实施控制。

由于变换的是矢量，所以这样的坐标变换也可称作矢量变换，相应的控制系统称为矢量控制（VC）系统或按转子磁链定向控制（FOC）系统。

2.按转子磁链定向的矢量控制方程及其解耦作用

上述只是矢量控制的基本思路，其中的矢量变换包括三相/两相变换和同步旋转变换。实际上，异步电动机包含定子和转子，定、转子电流都要变换，情况要复杂一些，还必须用动态数学模型来分析。
在进行两相同步旋转坐标变换时，只规定了d，q两轴的相互垂直
关系和与定子频率同步的旋转速度，并未规定两轴与电机旋转磁场的相对位置，对此是有选择余地的。现在d轴是沿着转子总磁链矢量的方向，并称之为M轴，而q 轴再逆时针转90°,即垂直于转子总磁链矢量，称之为T轴。这样的两相同步旋转坐标系就具体规定为 M，T 坐标系，即按转子磁链定向的坐标系。


下图中前述的等效直流电机模型被分解成 ω和Ψ_r两个子系统。可以看出，虽然通过矢量变换，将定子电流解耦成 i_sm和 i_st两个分量，但是，从 ω和Ψ_r两个子系统来看，由于Te同时受到 i_st和 Ψ_r 的影响，两个子系统仍旧是耦合着的。
按照矢量控制系统原理结构图模仿直流调速系统进行控制时，可设置磁链调节器AΨR和转速调节器ASR分别控制Ψ_r和ω 。
为了使两个子系统完全解耦，除了坐标变换以外，还应设法抵消转子磁链Ψ_r对电磁转矩Te的影响。比较直观的办法是，把ASR的输出信号除以Ψ_r。

当控制器的坐标反变换与电机中的坐标变换对消，且变频器的滞后作用可以忽略时，此处的（÷ Ψ_r ）便可与电机模型中的（x Ψ_r ）对消，两个子系统就完全解耦了。这时，带除法环节的矢量控制系统可以看成是两个独立的线性子系统，可以采用经典控制理论的单变量线性系统方法或相应的工程设计方法来设计两个调节器AΨR和ASR。
★应该注意，在异步电机矢量变换模型中的转子磁链 Ψ_r 和它的定向相位角 φ 都是实际存在的，而用于控制器的这两个量都难以直接检测，只能采用观测值或模型计算值，在图中冠以符号“^”以示区别。

3.转子磁链模型(转子磁链观测器)

要实现按转子磁链定向的矢量控制系统，很关键的因素是要获得转子磁链信号，以供磁链反馈和除法环节的需要。在过去人们曾采用尝试直接检测磁链的方法，如：在电机槽内埋设探测线圈，又或是②利用贴在定子内表面的霍尔元件或其它磁敏元件。从理论上：直接检测应该比较准确，但实际上这样做都会遇到不少工艺和技术问题，而且由于齿槽影响，使检测信号中含有较大的脉动分量，越到低速时影响越严重。现多采用间接计算的方法, 即利用容易测得的电压、电流或转速等信号，利用转子磁链模型，实时计算磁链的幅值与相位。

计算转子磁链的方法：
①电流模型：适合于低速，例如在两相静止坐标系上的转子磁链电流模型、在两相旋转坐标系上的转子磁链电流模型。
②电压模型：适合于中、高速。(低速时定子电阻压降影响大)
③组合模型：低速用电流模型，中、高速用电压模型。

八、基于动态模型按定子磁链控制的直接转矩控制系统

直接转矩控制系统简称DTC系统，是继矢量控制系统之后发展起来的另一种高动态性能的交流电动机变压变频调速系统。在它的转速环里面，利用转矩反馈直接控制电机的电磁转矩，因而得名。

1.直接转矩控制系统的原理和特点

结构特点：与VC系统一样，它也是分别控制异步电动机的转速和磁链（定子磁链）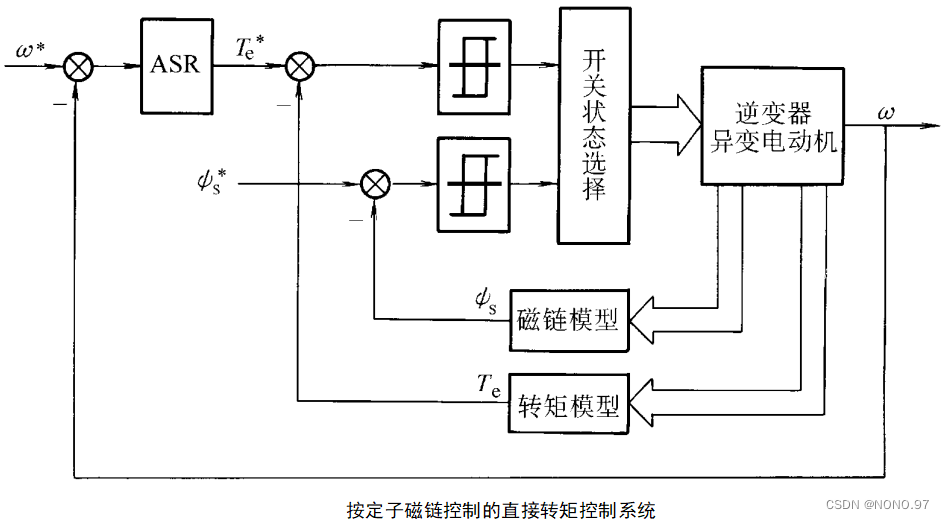

转速、磁链双闭环：ASR的输出作为电磁转矩的给定信号；设置转矩控制内环。
转矩和磁链的控制器：用滞环控制器(双位式砰-砰控制器)取代通常的PI调节器

DTC系统与VC系统不同的控制特点：
（1）转矩和磁链的控制采用双位式砰-砰控制器，并在PWM 逆变器中直接用这两个控制信号产生电压的SVPWM 波形，从而避开了将定子电流分解成转矩和磁链分量，省去了旋转变换和电流控制，简化了控制器的结构。
（2）选择定子磁链作为被控量，而不象VC系统中那样选择转子磁链，这样一来，计算磁链的模型可以不受转子参数变化的影响，提高了控制系统的鲁棒性。如果从数学模型推导按定子磁链控制的规律，显然要比按转子磁链定向时复杂，但是，由于采用了砰-砰控制，这种复杂性对控制器并没有影响。
（3）由于采用了直接转矩控制，在加减速或负载变化的动态过程中，可以获得快速的转矩响应，但必须注意限制过大的冲击电流，以免损坏功率开关器件，因此实际的转矩响应的快速性也是有限的。
从总体控制结构上看，直接转矩控制(DTC)系统和矢量控制(VC)系统是一致的，都是分别控制异步电动机的转速和磁链，都能获得较高的静、动态性能。

2.直接转矩控制系统的控制规律和反馈模型

除转矩和磁链砰-砰控制外，DTC系统核心问题是：转矩和定子磁链反馈信号的计算模型、如何根据两个砰-砰控制器的输出信号来选择电压空间矢量和逆变器的开关状态。


DTC系统存在的问题：
（1）由于采用砰-砰控制，实际转矩必然在上下限内脉动，而不是完全恒定的。
（2）由于磁链计算采用了带积分环节的电压模型，积分初值、累积误差和定子电阻的变化都会影响磁链计算的准确度。
这两个问题的影响在低速时都比较显著，因而使DTC系统的调速范围受到限制。

3.直接转矩控制系统与矢量控制系统的比较

DTC系统和VC系统都是已获实际应用的高性能交流调速系统。两者都采用转矩（转速）和磁链分别控制，这是符合异步电动机动态数学模型的需要的。但两者在控制性能上却各有千秋。
●VC系统强调Te与Ψr的解耦，有利于分别设计转速与磁链调节器。其次实行连续控制，可获得较宽的调速范围，但按Ψr 定向受电动机转子参数变化的影响，降低了系统的鲁棒性。
●DTC系统则实行Te 与Ψs 砰-砰控制，避开了旋转坐标变换，简化了控制结构；控制定子磁链而不是转子磁链，不受转子参数变化的影响；但不可避免地产生转矩脉动，低速性能较差，调速范围受到限制。

第三章——绕线转子异步电机双馈调速系统——转差功率馈送型调速系统

转差功率是研究异步电动机调速方法时所关心的问题，交流调速系统按转差功率的处理方式可分为三种类型。
（1）转差功率消耗型——异步电机采用调压等调速方式，转速越低时，转差功率的消耗越大，效率越低；但这类系统结构简单，备成本最低，所以有一定的应用价值。
（2）转差功率不变型——变频调速方法转差功率很小，而且不随转速变化，效率较高；但在定子电路中须配备与电动机容量相当的变压变频器，相比之下，设备成本最高。
（3）转差功率馈送型——控制绕线转子异步电动机的转子电压，利用其转差功率并达到调节转速的目的，这种调节方式具有良好的调速性能和效率；但要增加一些设备。
前两章已分别讨论了转差功率消耗型和不变型两种调速方法，本章将讨论转差功率馈送型调速方法。

一、异步电机双馈调速工作原理

1.双馈调速的概念和适用范围

（1）双馈调速适合的电机类型
在异步电机中，减少转差功率可提高电机效率。要利用转差功率，就必须使异步电动机的转子绕组有与外界实现电气联接的条件。因此，双馈调速适用于绕线转子异步电动机。
定义：定子功率和转差功率可以分别向定子和转子馈入，也可以从定子或转子输出，故称作双馈电机。
至于电功率是馈入定子绕组和/或转子绕组，还是由定子绕组和/或转子绕组馈出，则要视电机的工况而定。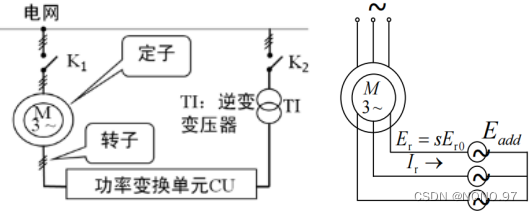

（2）双馈调速的概念和结构：所谓“双馈”，就是指把绕线转子异步电机的定子绕组与交流电网连接，转子绕组与其他含电动势的电路相连接，使它们可以进行电功率的相互传递。从电路拓扑结构上看，可认为是在转子绕组回路中附加一个交流电动势。

2.异步电机转子附加电动势的作用

结论：在绕线转子异步电动机的转子侧引入一个可控的附加电动势，就可调节电动机的转速。

3.异步电机的功率变换单元

前述提及：在转子侧引入一个可控的附加电动势即可以实现调速，该调速过程必然在转子侧有功率的传递。从功率传送的角度看，双馈调速是用控制异步电动机转子中转差功率的大小与流向来实现对电动机转速的控制。

异步电机的功率关系：
P_m = sP_m + (1 - s)P_m
P_m — 从定子传入转子(或由转子传出给定子)的电磁功率（气隙功率）
sP_m — 输入或输出转子电路的功率，即转差功率；
(1-s)P_m — 电机轴上输出或输入的功率，机械功率

串级调速的基本能量关系：是串入附加电动势，吸收转子降速引起的转差功率，并将吸收的功率回馈电网。

二、异步电机在次同步电动状态下的双馈系统——串级调速系统

在异步电机转子回路中附加交流电动势调速的关键就是在转子侧串入一个可变频、可变幅的电压。对于只用于次同步电动状态的情况来说，比较方便的办法是将转子电压先整流成直流电压，然后再引入一个附加的直流电动势，控制此直流附加电动势的幅值，就可以调节异步电动机的转速。这样，就把交流变压变频这一复杂问题，转化为与频率无关的直
流变压问题，对问题的分析与工程实现都方便多了。

为了满足平滑可调、节能（产生附加直流电动势的装置能够吸收从异步电动机转子侧传递来的转差功率并加以利用）的要求，本章采用工作在有源逆变状态的晶闸管可控整流装置 (有源逆变器) 作为产生附加直流电动势的电源。按照上述原理组成的异步电机在低于同步转速下作电动状态运行的双馈调速系统，习惯上称之为电气串级调速系统。

串级调速系统的工作原理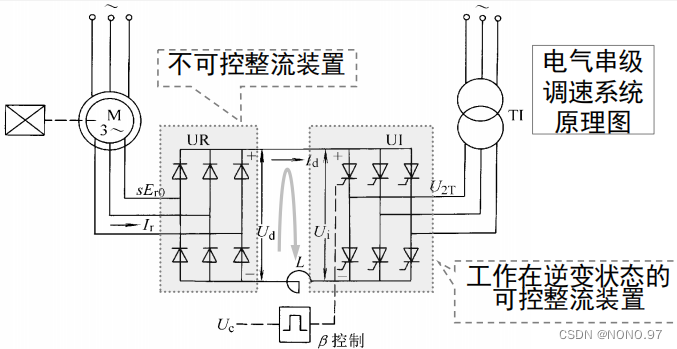

UR — 三相不可控整流装置，将异步电机转子相电动势 sE_r0整流为直流电压U_d。
UI — 三相可控整流装置，工作在有源逆变状态：可提供可调的直流电压 Ui ，作为电机调速所需的附加直流电动势；可将转差功率变换成交流功率，回馈到交流电网。
U_d = 2.34sE_r0，U_i = 2.34U_2Tcosβ
转子直流回路电压方程：2.34sE_r0 = 2.34U_2Tcosβ + I_dR，β为工作在逆变状态的可控整流装置UI的逆变角，R为转子直流回路总电阻。可见，转差率s与I_d和β有确定的关系。

（1）起动
●起动条件：起动应有足够大的转子电流Ir或足够大的整流后直流电流 I_d ，为此，转子整流电压U_d 与逆变电压U_i 间应有较大的差值。
●起动控制(起动过程特点：启动时s=1,随n增加，s降低)
•控制逆变角β 使在起动开始的瞬间，U_d与U_i 的差值能产生足够大的I_d ，以满足所需的电磁转矩，但又不超过允许的电流值，这样电动机就可在一定的动态转矩下加速起动。
•随着转速的增高，s下降，U_d随之下降，为维持加速时动态转矩基本恒定，则相应地增大β 角以减小值U_i 。

（2）调速
调速原理：通过改变β 角的大小调节电动机的转速。
调速过程：β↑ → U_i↓ → I_d↑ → T_e↑ → n↑ → K₁sE_r0↓ → I_d↓
直到2.34s₂E_r0 = 2.34U_T2cosβ₂ + I_dLR，系统稳定。此时 s₂ < s，升速。
同理减小β 角时可使电动机在降低了的转速下稳定运行。

（3）停车
串级调速系统没有制动停车功能。由于在串级调速系统中与转子连接的是不可控的整流装置，因此不可能向转子输入电功率，只能靠减小 β 角逐渐减速，并依靠负载阻转矩的作用自由停车。

（4）小结
●串级调速系统能够靠调节逆变角 β 实现平滑无级调速
●系统能把异步电动机的转差功率回馈给交流电网，从而使扣除装置损耗后的转差功率得到有效利用，大大提高了调速系统的效率。

三、异步电动机串级调速时的机械特性（不进行推导）

在串级调速系统中，异步电动机转子侧整流器的输出量U_d和I_d分别与异步电动机的转速和电磁转矩有关。因此，可以从电动机转子直流回路着手来分析异步电动机在串级调速时的机械特性。

（1）理想空载转速
在异步电动机转子回路串电阻调速时，其理想空载转速就是其同步转速，而且恒定不变，调速时机械特性变软，调速性能差。在串级调速系统中，由于电动机的极对数与旋转磁场转速都不变，因此同步转速也是恒定的，但是它的理想空载转速却能够连续平滑地调节。

●当系统在理想空载状态下运行时（I_d = 0），转子直流回路的电压平衡方程式变成： s₀ = U_T2cosβ / E_r0，其中，s₀ — 异步电动机在串级调速时对应于某一β角的理想空载转差率（变化）
●理想空载转速方程：n₀ = n_syn(1 - s₀) = n_syn(1 - U_T2cosβ / E_r0) ，式中 n_syn— 异步电动机的同步转速。
由上式可知，在串级调速时，理想空载转速与同步转速是不同的。当改变逆变角 β 时，理想空载转差率和理想空载转速都相应改变。除此之外，在不同的 β 角下，异步电动机串级调速时的机械特性是近似平行的，(s与Te曲线斜率不变)，其工作段类似于直流电动机变压调速的机械特性（随 β 的变化而变化）。

由此，总结出特征１:串级调速的同步转速是恒定的，但理想空载转速能够连续平滑地调节（随 β 的变化而变化）。

（2）机械特性的斜率与最大转矩
串级调速时，转子回路中接入了串级调速装置（包括两套整流装置、平波电抗器、逆变变压器等），实际上相当于在电动机转子回路中接入了一定数量的等效电阻和电抗，它们的影响在任何转速下都存在。
当电机在最高速的特性上( β = 90°)带额定负载，也难以达到其额定转速。
由此，总结出特征２：异步电动机串级调速时的机械特性是近似平行的，但比异步电动机的固有机械特性要软得多。

（3）由于转子回路电抗的影响, 整流电路换相重叠角将加大，并产生强迫延迟导通现象，使串级调速时的最大电磁转矩比电动机在正常接线时的最大转矩有明显的降低。
由此，总结出特征3：串级调速时的最大电磁转矩比电动机在正常接线时的最大转矩有明显的降低，（减少17.4%）。

四、串级调速系统的效率分析

（1）串级调速系统功率流程
在串级调速时，P_s未被全部消耗掉，而是扣除了转子铜损 P_Cur、杂散损耗和附加的串级调速装置损耗 P_tan后通过转子整流器与逆变器返回电网，这部分返回电网的功率称作回馈功率 P_f 。
对整个串级调速系统来说，它从电网吸收的净有功功率应为 P_in = P₁ – P_f 。
P_m = P₁ – P_cus -P_Fe，P_mech = （1 - s）P_m ，P_s = sP_m

（2）串级调速系统效率及比较

在串级调速系统中，当电动机的转速降低时，如果负载转矩不变， ∑p 和 p_tan都基本不变，分子和分母中的 Pm(1-s) 项随着 s 的增大而同时减少，对 η_sch 值的影响并不太大。忽略各种损耗时效率达100%。

（3）转子回路串电阻调速的效率
当电动机转子回路串电阻调速时，调速系统的效率是：

其中，P_m(1- s) 项随s 的变化和串级调速时一样，而所串电阻越大时，p_Cur 越大，∑p 也越大，因而效率 η_R 越低，几乎是随着转速的降低而成比例地减少。

（4）效率的比较
串级调速系统的总效率是比较高的，且当电动机转速降低时，η_sch 的减少并不多。而绕线转子异步电动机转子回路串电阻调速时的效率几乎随转速的降低而成比例地减少。

总结

小小的总结：

完成硬件部分的最后一门！历时好几天吧？(ಥ_ಥ) 反正比直流电机用时长，经过我的深抠之下，总算是完成了~~交流调速系统的知识虽然看起来很多而且很难，但它最侧重分析以及对知识点的理解（靠背和理解），总结起来费了不少劲，而且有很多公式推导，也不知道整理的意义何在，不过我反而对我自己有了更深的认识……由于老师要求我们不能将课件私自上传到网上，所以这里我就不向大家分享老师的PPT了，这篇文章是调速系统的最后一部分，也是我大规模更新的最后一章，之后我打算放飞一段时间，这段时间，为了赶这个，着实花了不少心思，现在电量仅有8的电，CSDN的实时保存还是很费电的。
我的隔离早已结束了，正常的校园生活回来啦，所以，这一阶段的总结就到此为止了，千言万语都不能表达我对此刻的欣喜若狂（主要是电脑只有百分之7的电了），毕竟总结知识点相当繁琐。这段时间非常感谢大家的支持！如果后边我还有空闲，那么我就试着更新软件部分。

学习附件

链接：https://pan.baidu.com/s/1TbCgggatPoXR-ZE2YEgOKA
提取码：osub