Unet网络

即卷积pad=0,这使得图像进行一次卷积会失去边界（图像一周）像素点。

木子kk

2493人浏览 · 2023-04-20 10:55:16

木子kk · 2023-04-20 10:55:16 发布

1、卷积与逆卷积

卷积是有一种，多对一的关系；
逆卷积是有一种，一对多的关系；

无填充卷积unpadded convolutions：即卷积pad=0,这使得图像进行一次卷积会失去边界（图像一周）像素点

1.1 卷积的三种类型

是对卷积核移动范围的不同限制

full mode：从filter和image刚相交开始做卷积，不足的部分padding 0。filter的运动范围如图所示。

same mode：当filter的中心(K)与image的边角重合时，开始做卷积运算，可见filter的运动范围比full模式小了一圈。注意：这里的same还有一个意思，卷积之后输出的feature map尺寸保持不变(相对于输入图片)。当然，same模式不代表完全输入输出尺寸一样，也跟卷积核的步长有关系。same模式也是最常见的模式，因为这种模式可以在前向传播的过程中让特征图的大小保持不变，调参不需要精准计算其尺寸变化(因为尺寸根本就没变化)。

valid mode：当filter全部在image里面的时候，进行卷积运算，可见filter的移动范围较same更小了。

1.2 反卷积（转置卷积）

输入图像通过卷积神经网络（CNN）提取特征后，输出的尺寸往往会变小，但是我们需要将图像恢复到原来的尺寸以便进行进一步的计算，整个扩大图像尺寸，实现图像由小分辨率到大分辨率的映射的操作，叫做上采样（Upsample）。反卷积是上采样的一种方式，反卷积也叫转置卷积。

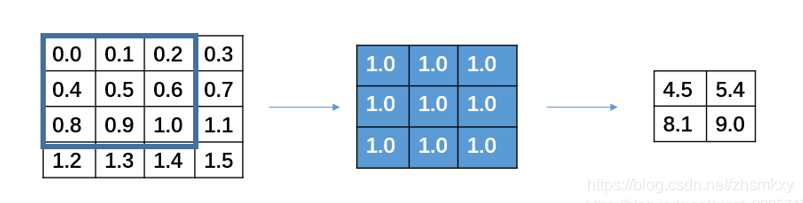
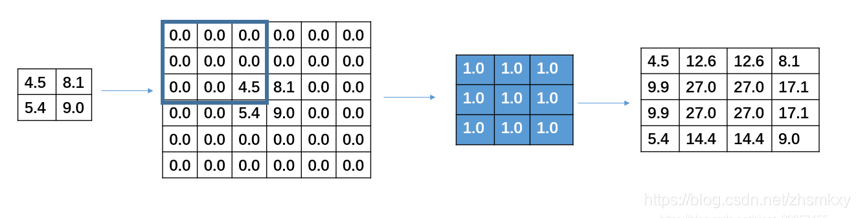
反卷积的工作过程，与卷积过程的主要区别在于反卷积输出的图片尺寸会大于输入图片的尺寸，通过增加padding来实现这一操作，下图展示的是一个stride为1的反卷积过程。在实际进行逆卷积的操作的时候，我们是会在input周围填充0

可以看到，在填充后，input左上角的方框会被计算9次，相当于是和output的9个数字是有关系的。

在进行反卷积的时候设置的stride并不是指反卷积在进行卷积时候卷积核的移动步长，而是被卷积矩阵填充的padding。比如下图中原输入是一个3×3的输入，此时要进行反卷积过程，且设置的stide=2，操作是在3×3的每一行每一列插入一行和一列的0的填充。

在这里插入图片描述

通过反卷积并不能还原之间的矩阵，只能从大小上进行还原，反卷积的本质还是卷积，只是在进行卷积之前，会进行一个自动的padding补充0，从而使得输出的矩阵和指定输出的矩阵的shape相同。

在这里插入图片描述

2、overlap-tile策略

医学图像是一般相当大，分割时候不可能将原图直接输入网络。所以需要用一个滑动窗口把原图扫一遍，使用原图的切片进行训练或测试。

在这里插入图片描述

红框是要分割区域。但是在切图时要包含周围区域，overlap一个重要原因是周围overlap部分可以为分割区域边缘部分提供纹理等信息。这样的策略会带来一个问题，图像边界的图像块没有周围像素，卷积会使图像边缘处的信息丢失。因此对周围像素采用了镜像扩充。图中红框部分为原始图片，其周围扩充的像素点均由原图沿白线对称得到。这样，边界图像块也能得到准确的预测。

但这样的操作会带来图像重叠问题，即第一块图像周围的部分会和第二块图像重叠。因此在卷积时只使用有效部分。可能的解释是使用valid卷积和crop裁剪，最终传到下一层的只有中间原先图像块（黄色框内）的部分。

3、弹性变换

弹性变化是对像素点各个维度产生（-1,1）区间的随机标准偏差，并用高斯滤波（0,sigma）对各维度的偏差矩阵进行滤波，最后用放大系数alpha控制偏差范围。因而由A（x，y）得到的A’(x+delta_x,y+delta_y)。A’的值通过在原图像差值得到，A’的值充当原来A位置上的值。一般来说，alpha越小，sigma越大，产生的偏差越小，和原图越接近。

因为unet论文的数据集是细胞组织的图像，细胞组织的边界每时每刻都会发生不规则的畸变，所以采用弹性变形的增广是非常有效的。

4、BiCubic（双三次插值）

假设源图像A大小为m*n，缩放K倍后的目标图像B的大小为M*N，即K=M/m。A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一像素点(X,Y)的值，必须先找出像素(X,Y)在源图像A中对应的像素(x,y)，再根据源图像A距离像素(x,y)最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数，利用BiCubic基函数求出16个像素点的权重，图B像素(x,y)的值就等于16个像素点的加权叠加。

根据比例关系x/X=m/M=1/K，我们可以得到B(X,Y)在A上的对应坐标为

A(x,y)=A(X*(m/M),Y*(n/N))=A(X/K,Y/K)。

如图所示P点就是目标图像B在(X,Y)处对应于源图像A中的位置，P的坐标位置会出现小数部分，所以我们假设 P的坐标为P(x+u,y+v)，其中x,y分别表示整数部分，u,v分别表示小数部分（蓝点到a11方格中红点的距离）。那么我们就可以得到如图所示的最近16个像素的位置，在这里用a(i,j)(i,j=0,1,2,3)来表示，如上图。

双立方插值的目的就是通过找到一种关系，或者说系数，可以把这16个像素对于P处像素值得影响因子找出来，从而根据这个影响因子来获得目标图像对应点的像素值，达到图像缩放的目的。BiCubic基函数形式如下：

这里写图片描述

要求出BiCubic函数中的参数x,从而获得16个像素所对应的权重W(x)。BiCubic基函数是一维的，而像素是二维的，所以将像素点的行与列分开计算。BiCubic函数中的参数x表示该像素点到P点的距离。
例如：a(0,0)距离P(x+u,y+v)的距离为(1+u,1+v)，因此a(0,0)的横坐标权重k_i_0=W(1+u)，纵坐标权重k_j_0=W(1+v)。

同理我们可以得到所有行和列对应的系数：

k_i_0=W(1+u), k_j_0=W(1+v)
k_i_1=W(u), k_j_1=W(v)

k__i_2=W(1-u), k_j_2=W(1-v)

k_i_3=W(2-u), k_j_3=W(2-v)

这样我们就分别得到了行和列方向上的系数。由k_i_j=k_i*k_j我们就可以得到每个像素a(i,j)对应的权值了。a(i,j)对B(X,Y)的贡献值为:

(aij像素值）* k_i_0*k_ j_0。

B(X,Y)像素值为:

$B(X,Y) = \sum_{i=0}^{3} \sum_{j=0}^{3} a_{ij} \times W(i) \times W(j)$

5、Momentum（动量）

梯度下降算法中，学习率太大，函数无法收敛，甚至发散。学习率足够小，理论上是可以达到局部最优值的（非凸函数不能保证达到全局最优），但学习率太小却使得学习过程过于缓慢。合适的学习率应该是能在保证收敛的前提下，能尽快收敛。

对于深度网络中，参数众多，参数值初始位置随机，同样大小的学习率，对于某些参数可能合适，对另外一些参数可能偏小（学习过程缓慢），对另外一些参数可能太大（无法收敛，甚至发散）。而学习率一般而言对所有参数都是固定的，所以无法同时满足所有参数的要求。通过引入Momentum可以让那些因学习率太大而来回摆动的参数，梯度能前后抵消，从而阻止发散。

进一步讲解：深度学习入门之Momentum_深度学习momentum_赵孝正的博客-CSDN博客

6、Unet模型

因为网络的结构很像个U，所以称为Unet。Unet 网络是针对像素点的分类，判断像素点输属于前景还是背景。

下采样：通过减少图像size，增加图像channel来提取特征。

上采样：将逐步还原图像的size，上采样的输入特征图不仅仅是上一步的输出，还包含了左边对应特征信息。

蓝色箭头代表3x3的卷积操作，并且stride是1，padding策略是vaild，因此，每个该操作以后，featuremap的大小会减2。
红色箭头代表2x2的maxpooling操作，需要注意的是，此时的padding策略也是vaild，这就会导致如果pooling之前featuremap的大小是奇数，会损失一些信息。所以要选取合适的输入大小，因为2*2的max-pooling算子适用于偶数像素点的图像长宽。
绿色箭头代表2x2的反卷积操作，会将featuremap的大小乘2。
反卷积过后，将反卷积的结果与编码部分中对应步骤的特征图拼接起来(concat)（也就是将深层特征与浅层特征进行融合，使得信息变得更丰富）。（白/蓝块）
灰色箭头表示复制和剪切操作，可以发现，在同一层左边的最后一层要比右边的第一层要大一些，这就导致了，想要利用浅层的feature，就要进行一些剪切。左边深蓝虚线部分就是要裁剪的部分，它对应右边的白色长方块部分。
输出的最后一层，使用了1x1的卷积层做了分类。将64通道的特征图转化为特定类别数量（分类数量）的结果。

对feature map,一个大小为256*256*64的feature map(w为256，h为256，c为64)，和一个大小为256*256*32的feature map进行Concat融合，你就会得到一个大小为256*256*96的feature map
在实际使用中，Concat融合的两个feature map的大小不一定相同，例如256*256*64的feature map和240*240*32的feature map进行Concat，有两种方法：

将大的256*256*64的feature map进行裁剪，裁剪为240*240*64的feature map，比如上下左右，各舍弃8 pixel，裁剪后再进行Concat，得到24024096的feature map。
将小的240*240*32的feature map进行padding操作，padding为256*256*32的feature map，比如上下左右，各补8 pixel，padding后再进行Concat，得到25625696的feature map。

UNet采用的Concat方案就是第二种，将小的feature map进行padding，padding的方式是补0，一种常规的常量填充。

7、评价指标

7.1 pixel error

评估分割的最简单方法是测量原始标签和分割标签之间的像素误差。让 $L_{i}$ 表示图像位置 i 处边界标记 L 的值。L 相对于另一个二进制标记 $L^{*}$ 的像素误差是两个标记不一致的像素位置数。这也可以写成欧几里得距离的平方 $||L - L^{*}||^{2}$ ，这相当于汉明距离，因为标签是二进制值的。

pixel error虽简单，但它对边界位置的微小位移过于敏感，即使将一种人类边界标记与另一种人类边界标记进行比较，这种位移也无处不在。这些分歧不会导致图像解释的质差异，但可能导致像素误差的巨大定量差异。

warping error 和 Rand error则相对缓和，更倾向于形态和整体的分割质量，在生物医学图像分割上是较为合理的评价指标。

7.2 Warping error

warping error是基于拓扑不变性衡量分割质量。

如果 $L^{*}$ 可以通过一系列像素翻转转换为 L，则每个像素

保留一组所需的拓扑属性仅出现在掩码 M 内的位置
仅出现在掩码 M 内的位置

那我们就会说L是 $L^{*}$ 的warping，或者 $L\triangleright L^{*}$ 。第一个条件约束 L 和 $L^{*}$ 在拓扑上等价。第二个条件可用于约束 L 在几何上与 $L^{*}$ 相似。

将ground truth $L^{*}$ 保留拓扑不变性（没有分裂、合并、产生或消去空洞、增加或减少物体数量等），并只在一定范围产生像素变化，得到许多L，计算预测输出T和 L 间的最小距离作为warping error结果。

In other words, the warping error between two segmentations is the minimum mean square error between the pixels of the target segmentation and the pixels of a topology-preserving warped source segmentation.

7.3 Rand error

Rand error是根据Rand Index而来，是一种聚类的评价指标。即将分割看做是一种对像素的聚类过程，来衡量分割质量。

7.3.1 Rand Index（RI）

兰德指数需要给定实际类别信息C，假设K是聚类结果，a表示在C与K中都是同类别的元素对数，b表示在C与K中都是不同类别的元素对数。评价同一object在两种分类结果中是否被分到同一类别。

计算方法1：列举法

对于数据a和b而言：

X：都被归为了第1类

Y：都被归为了第2类

同理，对于数据a和c而言：

X：分别被归为了第1和2类，不是同一类

Y：分别被归为了第2和3类，不是同一类

所以数据a和c对于算法X和算法Y来说是一致的。

以这个上述数据为例，则所有pair结果如下：

一致的对数有7对，总对数有10对，所以 Rand Index = 7/10=0.7

计算方法2：混淆矩阵

如果我们把这三个簇想象成三个黑色的布袋。那么对于任意一个布袋来说：

如果你从里面任取两个样本出来均是同一个类别，这就表示这个布袋中的所有样本都算作是聚类正确的
如果你从里面任取两个样本出来不是同一个类别，这就表示这个布袋中的部分样本是算作是聚类错误的

其次，对于任意两个布袋来说：

如果你任意从两个布袋中各取一个样本发现两者均是不同类别，这就表示两个布袋中的样本都被聚类正确了
如果你任意从两个布袋中各取一个样本发现两者均是相同类别，这就表示两个布袋中的样本有的被聚类错误了

由此，可以做出如下定义：

TP：表示两个同类样本点在同一个布袋中的情况数量；

FP：表示两个非同类样本点在同一个布袋中的情况数量；

TN：表示两个非同类样本点分别在两个布袋中的情况数量；

FN：表示两个同类样本点分别在两个布袋中的情况数量；

则RI的计算公式为：

RI的取值范围：（0,1），RI越大表示聚类效果越好。

我们先计算TP值，根据例子图所示，很容易计算出该结果，其含义是：

Cluster1中：5个绿色三角中取2个

Cluster2中：4个蓝色圆形中取2个

Cluster3中：3个红色正方形中取2个

Cluster3中：2个绿色三角中取2个

而接下来的FP、TN和FN好像都不怎么好计算，不过我们可以换个思路，直接联合计算：

TP+FP：实际上就是从同一个布袋中取2个样本的数目

TP+FN：实际上就是任意两个同类样本点分布在同一个簇和非同一个簇的所有情况总和，也就是找出随便从同类样本中抽2个样本的所有情况（在同一个cluster和不在同一个cluster）

TP+FP+TN+FN：该值其实是所有样本中随机抽2个样本

根据这些组合结果以及TP的值，我们便可以得到混淆矩阵的所有结果

根据公式可计算出RI = 92/136 =0.6765

7.3.2 调整 Rand Index（ARI）

RI在极端的情况下，例如把17个样本分成17个类，若TP=0，FP=0，FN=44，TN=92，此时RI=92/136 =0.6765，这是因为聚类过于严格，导致每个样本单独成类，理论上我们认为这种聚类是不好的，它与把样本分成3类有一样的RI值。为了解决这个问题，引入了ARI。

在计算调整兰德系数时，思路会发生一定的改变。我们此时不依赖于混淆矩阵，而是比较聚类算法得到的标签和自身真实标签之间的差异。

C：根据聚类算法得到的聚类结果，C1,C2…Cr一共r种聚类结果

T：根据真实标签得到的真实结果，T1,T2…Tc一共c种真实结果

Xr, c：每种情况下相交的统计数值

则ARI的计算公式如下：

还是之前的例子：

我们用T1表示绿色的三角，T2表示蓝色的圆形，T3表示红色的正方形：

计算ARI的过程如下：

有数学家证明，ARI其实可以通过混淆矩阵直接计算得到：

两种方法得到的结果是一样的。

7.3.2 Rand error

Rand error定义 $S_{1}$ 和 $S_{2}$ 表示图片 $I$ 上的两个分割的结果。图片 $I$ 包括 n 个像素，不同位置的像素两两配对，共有 $C_{n}^{2}$ 个像素对。定义 $a$ 表示在 $S_{1}$ 和 $S_{2}$ 上都属于同一类的像素对数量。 $b$ 表示在 $S_{1}$ 和 $S_{2}$ 上都属于不同类的像素对数量。Rand Index（兰德指数）的计算公式为：

Rand error （RE）是两个分割在一对像素属于相同还是不同对象方面存在分歧的频率，计算公式如下为：

7.3.4 Warping error 和 Rand error

乍一看，warping error似乎只测量边界检测性能。但它也是衡量细分性能的良好指标。这是因为数字拓扑告诉我们任何单个像素如何影响图像的全局拓扑。warping error是 T 中拓扑相关边界标注误差数量的上限（如果使用几何掩码，则warping error还包括几何性质的标注误差）。因此，如果通过找到它们的连接分量从T和 $L^{*}$ 生成分割，那么warping error应该是分割之间拓扑分歧的合理度量。

rand error可用于比较分割，其中区域是非连续像素聚类。这种分割不等同于边界标记，因此无法应用warping error。在许多应用中，这不是一个重要的限制。

在其他方面，warping error可以与rand error区分开来。warping error可以惩罚所有类型的拓扑错误，包括孔和手柄的存在，但rand error只会惩罚连接错误。在某些医学成像情况下，对拓扑的这些方面的控制尤为重要。rand error会轻微地惩罚边界位置的变化，而warping error则完全忽略它们。warping error根据误差本身涉及的像素数对拓扑误差进行加权，而rand error根据与误差关联的对象中的像素数对拆分或合并进行加权

7.4 IoU（交并比）

IoU通常被应用在目前目标检测算法的评价中，IOU值越高，说明算法对目标的预测精度越高。

假设分子的两个集合，一个集合是Ground Truth，另外一个集合是神经网络给出的预测值。不要被图中的正方形的形状限制了想想，对于分割任务来说，一般是像素级的不规则图案。如果预测正确，也就是分子中的蓝色交汇的部分，称之为True Positive，属于True Positive的像素的数量就是分子的值。分母的值是Ground Truth的所有像素的数量和预测结果中所有像素的数量的和再减去重叠的部分的像素数量。

对于IoU的预测好坏的直观理解就是：重叠的越多，IoU越接近1，预测效果越好

参考：

【图像分割】Unet系列深度讲解（FCN、UNET、UNET++）

什么是反卷积（快速理解）_丶夜未央丶的博客-CSDN博客

UNet网络解读_joejoeqian的博客-CSDN博客

[深度学习] 增加样本——弹性变换算法实现_lhanchao的博客-CSDN博客

论文原文： https://arxiv.org/pdf/1505.04597.pdf

双三次插值（BiCubic插值）_bicubic函数_咖喱姬姬的博客-CSDN博客

图像缩放之双三次插值法_淡雅与立夏的博客-CSDN博客

U-Net网络理解与应用_u-net优点_梅森姑娘的博客-CSDN博客

U-Net - 知乎

Topology preserving warping error

评价聚类的指标：纯度、兰德系数以及调整兰德系数 - 简书

如若侵权，请私信我，谢谢。

2048 AI社区

有“AI”的1024 = 2048，欢迎大家加入2048 AI社区

更多推荐

UFW防火墙安全指南

UFW（Uncomplicated Firewall）是Ubuntu/Debian系统中简化防火墙管理的工具，通过直观命令帮助用户有效控制网络流量，提升系统安全性。文章详细介绍了UFW的基本命令，包括启停防火墙、添加规则、限制连接速率和日志配置等操作，并提供了安全最佳实践，如默认拒绝策略、IP地址限制和服务级规则管理。同时，还涵盖高级配置技巧，例如多网络接口设置、规则优先级调整、IPv6支持及与f