1、案例概述

1.1 任务描述

随着电信行业的不断发展，运营商们越来越重视如何扩大其客户群体。据研究，获取新客户所需的成本远高于保留现有客户的成本，因此为了满足在激烈竞争中的优势，保留现有客户成为一大挑战。对电信行业而言，可以通过数据挖掘等方式来分析可能影响客户决策的各种因素，以预测他们是否会产生流失（停用服务、转投其他运营商等）。

1.2 研究背景

1. 通过对用户流失的预测能够有效的降低营销的成本，同时新用户的开发成本远高于保留现有客户成本；
2. 明确增值服务，给予更好的用户体验；
3. 有效区分价格敏感型何价格非敏感型客户，为公司获取更高的销售回报。

1.3 数据集

使用数据集来自Kaggle平台，可以从这里下载。数据集一共提供了7043条用户样本，每条样本包含21列属性，由多个维度的客户信息以及用户是否最终流失的标签组成，客户信息具体如下：
基本信息：包括性别、年龄、经济情况、入网时间等；
开通业务信息：包括是否开通电话业务、互联网业务、网络电视业务、技术支持业务等；
签署的合约信息：包括合同年限、付款方式、每月费用、总费用等。

1.4 方法概述

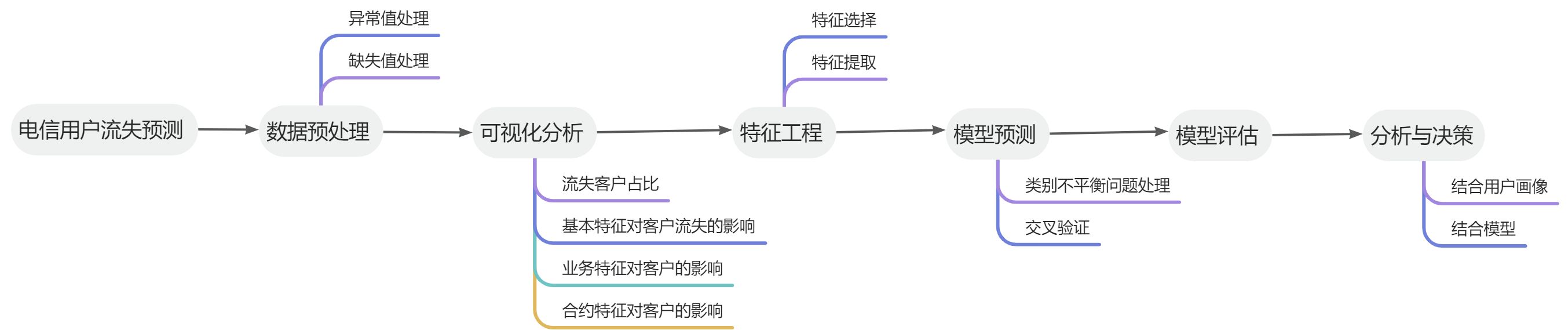
2、数据介绍

2.1 数据读取

import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings('ignore') #  忽略弹出的warnings信息

data = pd.read_csv('G:/study/数据分析训练集/datasets银行信用评估/datasets/Telco-Customer-Churn.csv')
df = pd.read_csv('G:/study/数据分析训练集/datasets银行信用评估/datasets/Telco-Customer-Churn.csv')
pd.set_option('display.max_columns', None)    # 显示所有列
data.head(10)
df.head(10)

2.2 数据观察

变量名	描述	数据类型	取值	所属特征群或标签
customerID	客户ID	字符串	7043个不重复取值	基本信息
gender	性别	字符串	Male，Female	基本信息
SeniorCitizen	是否为老人	整型	1，0	基本信息
Partner	是否有配偶	字符串	Yes，No	基本信息
Dependents	是否有家属	字符串	Yes，No	基本信息
tenure	入网月数	整型	0~72	基本信息
PhoneService	是否开通电话业务	字符串	Yes，No	开通业务信息
MultipleLines	是否开通多线业务	字符串	Yes，No，No phone service	开通业务信息
InternetService	是否开通互联网业务	字符串	DSL数字网络，Fiber optic光纤网络，No	开通业务信息
OnlineSecurity	是否开通在线安全业务	字符串	Yes，No，No Internet service	开通信息业务
OnlineBackup	是否开通在线备份业务	字符串	Yes，No，No Internet service	开通信息业务
DeviceProtection	是否开通设备保护业务	字符串	Yes，No，No Internet service	开通信息业务
TechSupport	是否开通技术支持业务	字符串	Yes，No，No Internet service	信息开通业务
StreamingTV	是否开通网络电视业务	字符串	Yes，No，No Internet service	信息开通业务
StreamingMocies	是否开通网络电影业务	字符串	Yes，No，No Internet service	信息开通业务
Contract	合约期限	字符串	Month-to-month，One year，Two year	签署的合约信息
PaperlessBilling	是否采用电子结算	字符串	Yes，No	签署的合约信息
PaymentMethod	付款方式	字符串	Bank transfer（automatic），Credit card（automatic），Electronic check，Mailed check	签署的合约信息
MonthlyCharges	每月费用	浮点型	18.25~118.75	签署的合约信息
TotalCharges	总费用	字符串	有部分空格字符，除此之外的字符串对应的浮点数取值范围在18.80~8684.80之间	签署的合约信息
Chum	客户是否流失	字符串	Yes,No	目标变量

3、数据预处理

查看数据当中是否存在缺失值。

dupNum = data.shape[0] - data.drop_duplicates().shape[0]
print("数据集中有%s列重复值" % dupNum)

没有重复值，继续进行下一步。

3.1 缺失值处理

统计数据集中缺失值情况：

data.isnull().any()

统计结果显示数据集当中没有存在缺失值，但是可能存在这样一种情况：采用
‘Null’，‘NaNcy’，‘ ’等字符（串）表示缺失，数据集中就有这样一列TotalCharges特征，存在如下所示的11条样本，其特征值为空格字符串（‘ ’）：

# 查看TotalCharges的缺失值
data[data['TotalCharges'] == ' '][['MonthlyCharges', 'TotalCharges']]

对于TotalCharges这列原本为字符串类型的特征，由于其特征值含有数值意义，应该首先将其转换为数值形式（浮点数）。此外，对其中不可转换的空格字符，可以用conwert_objects()函数转换成标准的数值型缺失值NaNcy。

#  convert_numeric如果为True，则尝试强制转换为数字，不可转换的变为NaN
data['TotalCharges'] = data['TotalCharges'].apply(pd.to_numeric, errors='coerce') 

print("此时TotalCharges是否已经转换为浮点型：", data['TotalCharges'].dtype == 'float')
print("此时TotalCharges存在%s行缺失样本。" % data['TotalCharges'].isnull().sum())

传统方法较常采用固定值来进行数值型特征的缺失值补充，我们先采用0进行补充：

# 固定值填充
fnDf = data['TotalCharges'].fillna(0).to_frame()

print("如果采用固定值填充方法还存在%s行缺失样本。" % fnDf['TotalCharges'].isnull().sum())

更进一步的，可以发现缺失样本左手拿个tenure特征（表示客户的入网时间）均为0，且在整个数据集中tenure为0与TotalCharges为缺失值是一一对应的。结合实际业务分析，这些样本对应的客户可能当月就流失了，但仍然要收取当月的费用，因此总费用即为该用户的每月费用（MonthlyCharges）。因此最终采用MonthlyCharges的数值对TotalCharges进行填充。

# 用MonthlyCharges的数值填充TotalCharges的缺失值
data['TotalCharges'] = data['TotalCharges'].fillna(data['MonthlyCharges'])    

data[data['tenure'] == 0][['MonthlyCharges', 'TotalCharges']]    # 观察处理后缺失值变化情况

3.2 异常值处理

查看数值类特征的统计信息：

data.describe()

数据集中大部分为类别型特征，上表中的SeniorCitizen特征取值只有0和1,也可视为类别特征。因此只有tenure、MonthlyCharges是数值特征，继续结合箱型图进行分析：

# 箱型图观察异常值情况
import seaborn as sns
import matplotlib.pyplot as plt    # 可视化
# 在Jupyter notebook里嵌入图片
%matplotlib inline

# 分析百分比特征
fig = plt.figure(figsize=(15,6)) # 建立图像

# tenure特征
ax1 = fig.add_subplot(311)    # 子图1
list1 = list(data['tenure'])
ax1.boxplot(list1, vert=False, showmeans=True, flierprops = {"marker":"o","markerfacecolor":"steelblue"})
ax1.set_title('tenure')

# MonthlyCharges特征
ax2 = fig.add_subplot(312)    # 子图2
list2 = list(data['MonthlyCharges'])
ax2.boxplot(list2, vert=False, showmeans=True, flierprops = {"marker":"o","markerfacecolor":"steelblue"})
ax2.set_title('MonthlyCharges')

# TotalCharges
ax3 = fig.add_subplot(313)    # 子图3
list3 = list(data['TotalCharges'])
ax3.boxplot(list3, vert=False, showmeans=True, flierprops = {"marker":"o","markerfacecolor":"steelblue"})
ax3.set_title('TotalCharges')

plt.tight_layout(pad=1.5)    # 设置子图之间的间距
plt.show() # 展示箱型图

由箱型图直观可见，这三列数值特征值均不含离群点（即异常值）。同时，其他类别特征的取值也未见异常，因此不需要进行异常值处理。

4、可视化分析

4.1 流失客户占比

# 观察是否存在类别不平衡现象
p = data['Churn'].value_counts()    # 目标变量正负样本的分布

plt.figure(figsize=(10,6))    # 构建图像

# 绘制饼图并调整字体大小
patches, l_text, p_text = plt.pie(p,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
# l_text是饼图对着文字大小，p_text是饼图内文字大小
for t in p_text:
    t.set_size(15)
for t in l_text:
    t.set_size(15)
    
plt.show()    # 展示图像

由饼状图课件，流失用户占比26.54，存在类别不平衡现象，后续需要进行相应处理。

4.2 基本特征对客户流失影响

### 性别、是否老年人、是否有配偶、是否有家属等特征对客户流失的影响
baseCols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents']

for i in baseCols:
    cnt = pd.crosstab(data[i], data['Churn'])    # 构建特征与目标变量的列联表
    cnt.plot.bar(stacked=True)    # 绘制堆叠条形图，便于观察不同特征值流失的占比情况
    plt.show()    # 展示图像

由图可知：
1、性别对客户流失基本没有影响；
2、年龄对客户流失有影响，老年人流失占比高于年轻人；
3、是否有配偶对客户流失有影响，无配偶客户流失占比高于有配偶客户；
4、是否有家属对客户流失有影响，无家属客户流失高于有家属客户。

### 观察流失率与入网月数的关系
# 折线图
groupDf = data[['tenure', 'Churn']]    # 只需要用到两列数据
groupDf['Churn'] = groupDf['Churn'].map({'Yes': 1, 'No': 0})    # 将正负样本目标变量改为1和0方便计算
pctDf = groupDf.groupby(['tenure']).sum() / groupDf.groupby(['tenure']).count()    # 计算不同入网月数对应的流失率
pctDf = pctDf.reset_index()    # 将索引变成列

plt.figure(figsize=(10, 5))
plt.plot(pctDf['tenure'], pctDf['Churn'], label='Churn percentage')    # 绘制折线图
plt.legend()    # 显示图例
plt.show()

pctDf.head()

由图可知：除刚入网（tenure=0）的客户之外，流失率随着入网时间的延长呈下降趋势；当入网超过两个月时，流失率小于留存率，这段时间可以看作用户的适应期。

4.3 业务特征对客户流失的影响

# 电话业务
posDf = data[data['PhoneService'] == 'Yes']
negDf = data[data['PhoneService'] == 'No']

fig = plt.figure(figsize=(10,4)) # 建立图像

ax1 = fig.add_subplot(121)
p1 = posDf['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (PhoneService = Yes)')

ax2 = fig.add_subplot(122)
p2 = negDf['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (PhoneService = No)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

由图可知，是否开通电话业务对客户流失影响很小。

# 多线业务
df1 = data[data['MultipleLines'] == 'Yes']
df2 = data[data['MultipleLines'] == 'No']
df3 = data[data['MultipleLines'] == 'No phone service']

fig = plt.figure(figsize=(15,4)) # 建立图像

ax1 = fig.add_subplot(131)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (MultipleLines = Yes)')

ax2 = fig.add_subplot(132)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (MultipleLines = No)')

ax3 = fig.add_subplot(133)
p3 = df3['Churn'].value_counts()
ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax3.set_title('Churn of (MultipleLines = No phone service)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

由图可知，是否开通多线业务对客户流失影响很小。此外MultipleLines取值为‘No’和‘No phone service’的两种情况基本一致，后续可以合并在一起。

# 互联网业务
cnt = pd.crosstab(data['InternetService'], data['Churn'])    # 构建特征与目标变量的列联表
cnt.plot.barh(stacked=True, figsize=(15,6))    # 绘制堆叠条形图，便于观察不同特征值流失的占比情况
plt.show()    # 展示图像

由图可知，未开通互联网的客户总数最少，而流失比例最低（7.40%）；开通光纤网络的客户总数最多，流失比例也最高（41.89%）；开通数字网络的客户则剧中（18.96%）。可以推测应该有更深层次的因素导致光纤用户流失更多的客户，下一步观察与互联网相关的各项业务。

# 与互联网相关的业务
internetCols = ['OnlineSecurity', 'OnlineBackup', 'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies']

for i in internetCols:
    df1 = data[data[i] == 'Yes']
    df2 = data[data[i] == 'No']
    df3 = data[data[i] == 'No internet service']

    fig = plt.figure(figsize=(10,3)) # 建立图像
    plt.title(i)
    
    ax1 = fig.add_subplot(131)
    p1 = df1['Churn'].value_counts()
    ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))    # 开通业务

    ax2 = fig.add_subplot(132)
    p2 = df2['Churn'].value_counts()
    ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))    # 未开通业务

    ax3 = fig.add_subplot(133)
    p3 = df3['Churn'].value_counts()
    ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))    # 未开通互联网业务
  
    plt.tight_layout()    # 设置子图之间的间距
    plt.show() # 展示饼状图

由图可知：所有互联网相关业务中未开通互联网的客户流失率均为7.40%，可以判断原因是上述六列特征均只在客户开通互联网业务之后才有实际意义，因而不会影响未开通互联网的客户；开通了这些新业务之后，用户的流失率会有不同程度的降低，可以认为多绑定业务有助于用户的留存；'StreamingTV’和 'StreamingMovies’两列特征对客户流失基本没有影响。此外，由于 ‘No internet service’ 也算是 ‘No’ 的一种情况，因此后续步骤中可以考虑将两种特征值进行合并。

4.4 合约特征对客户流失影响

# 合约期限
df1 = data[data['Contract'] == 'Month-to-month']
df2 = data[data['Contract'] == 'One year']
df3 = data[data['Contract'] == 'Two year']

fig = plt.figure(figsize=(15,4)) # 建立图像

ax1 = fig.add_subplot(131)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (Contract = Month-to-month)')

ax2 = fig.add_subplot(132)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (Contract = One year)')

ax3 = fig.add_subplot(133)
p3 = df3['Churn'].value_counts()
ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax3.set_title('Churn of (Contract = Two year)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

由图可知：合约期限越长，用户的流失率越低。

# 是否采用电子结算
df1 = data[data['PaperlessBilling'] == 'Yes']
df2 = data[data['PaperlessBilling'] == 'No']

fig = plt.figure(figsize=(10,4)) # 建立图像

ax1 = fig.add_subplot(121)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (PaperlessBilling = Yes)')

ax2 = fig.add_subplot(122)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (PaperlessBilling = No)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

由图可知：采用电子结算的客户流失率较高，原因可能时电子结算多为按月支付的形式。

# 付款方式
df1 = data[data['PaymentMethod'] == 'Bank transfer (automatic)']    # 银行转账（自动）
df2 = data[data['PaymentMethod'] == 'Credit card (automatic)']    # 信用卡（自动）
df3 = data[data['PaymentMethod'] == 'Electronic check']    # 电子支票
df4 = data[data['PaymentMethod'] == 'Mailed check']    # 邮寄支票

fig = plt.figure(figsize=(10,8)) # 建立图像

ax1 = fig.add_subplot(221)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (PaymentMethod = Bank transfer')

ax2 = fig.add_subplot(222)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (PaymentMethod = Credit card)')

ax3 = fig.add_subplot(223)
p3 = df3['Churn'].value_counts()
ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax3.set_title('Churn of (PaymentMethod = Electronic check)')

ax4 = fig.add_subplot(224)
p4 = df4['Churn'].value_counts()
ax4.pie(p4,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax4.set_title('Churn of (PaymentMethod = Mailed check)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

由图可知：四种付款方式中采用电子支票的客户流失率远高于其他三种。

# 每月费用核密度估计图
plt.figure(figsize=(10, 5))    # 构建图像

negDf = data[data['Churn'] == 'No']
sns.distplot(negDf['MonthlyCharges'], hist=False, label= 'No')
posDf = data[data['Churn'] == 'Yes']
sns.distplot(posDf['MonthlyCharges'], hist=False, label= 'Yes')

plt.show()    # 展示图像

# 总费用核密度估计图
plt.figure(figsize=(10, 5))    # 构建图像

negDf = data[data['Churn'] == 'No']
sns.distplot(negDf['TotalCharges'], hist=False, label= 'No')
posDf = data[data['Churn'] == 'Yes']
sns.distplot(posDf['TotalCharges'], hist=False, label= 'Yes')

plt.show()    # 展示图像

由图可知：客户的流失率的基本趋势是随每月费用的增加而增长，这与实际业务较为符合；当客户的总费用积累越多，流失率越低，这说明这些客户已经称为稳定的客户，不会轻易流失；此外，当每月费用处于70～110之间时流失率较高。

5、特征工程

5.1 特征提取

### 数值特征标准化
from sklearn.preprocessing import StandardScaler    # 导入标准化库

'''
注：

新版本的sklearn库要求输入数据是二维的，而例如data['tenure']这样的Series格式本质上是一维的
如果直接进行标准化，可能报错 "ValueError: Expected 2D array, got 1D array instead"
解决方法是变一维的Series为二维的DataFrame，即多加一组[]，例如data[['tenure']]
'''
scaler = StandardScaler()
data[['tenure']] = scaler.fit_transform(data[['tenure']])
data[['MonthlyCharges']] = scaler.fit_transform(data[['MonthlyCharges']])
data[['TotalCharges']] = scaler.fit_transform(data[['TotalCharges']])

data[['tenure', 'MonthlyCharges', 'TotalCharges']].head()    # 观察此时的数值特征

将数值特征缩放到同一尺度下，避免对特征重要性产生误判。

### 类别特征编码
# 首先将部分特征值进行合并
data.loc[data['MultipleLines']=='No phone service', 'MultipleLines'] = 'No'

internetCols = ['OnlineSecurity', 'OnlineBackup', 'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies']
for i in internetCols:
    data.loc[data[i]=='No internet service', i] = 'No'

print("MultipleLines特征还有%d条样本的值为 'No phone service'" % data[data['MultipleLines']=='No phone service'].shape[0])
print("OnlineSecurity特征还有%d条样本的值为 'No internet service'" % data[data['OnlineSecurity']=='No internet service'].shape[0])
print("...")

# 部分类别特征只有两类取值，可以直接用0、1代替；另外，可视化过程中发现有四列特征对结果影响可以忽略，后续直接删除
# 选择特征值为‘Yes’和 'No' 的列名
encodeCols = list(data.columns[3: 17].drop(['tenure', 'PhoneService', 'InternetService', 'StreamingTV', 'StreamingMovies', 'Contract']))     
for i in encodeCols:
    data[i] = data[i].map({'Yes': 1, 'No': 0})    # 用1代替'Yes’，0代替 'No'
# 顺便把目标变量也进行编码    
data['Churn'] = data['Churn'].map({'Yes': 1, 'No': 0})

# 其他无序的类别特征采用独热编码    
onehotCols = ['InternetService', 'Contract', 'PaymentMethod']
churnDf = data['Churn'].to_frame()    # 取出目标变量列，以便后续进行合并
featureDf = data.drop(['Churn'], axis=1)    # 所有特征列

for i in onehotCols:
    onehotDf = pd.get_dummies(featureDf[i],prefix=i) 
    featureDf = pd.concat([featureDf, onehotDf],axis=1)    # 编码后特征拼接到去除目标变量的数据集中

data = pd.concat([featureDf, churnDf],axis=1)    # 拼回目标变量，确保目标变量在最后一列
data = data.drop(onehotCols, axis=1)    # 删除原特征列

5.2 特征选择

'customerID’特征的每个特征值都不同，因此对模型预测不起贡献，可以直接删除。 ‘gender’、‘PhoneService’、‘StreamingTV’ 和 ‘StreamingMovies’ 则在可视化环节中较为明显地观察到其对目标变量的影响较小，因此也删去这四列特征。

# 删去无用特征 'customerID'、'gender'、 'PhoneService'、'StreamingTV'和'StreamingMovies'
data = data.drop(['customerID', 'gender', 'PhoneService', 'StreamingTV', 'StreamingMovies'], axis=1)
data.head(10)    # 观察此时的数据集

此外，还可以采用相关系数矩阵衡量连续型特征之间的相关性、用卡方检验衡量离散型特征与目标变量的相关关系等等，从而进行进一步的特征选择。例如，可以对数据集中的三列连续型数值特征 ‘tenure’, ‘MonthlyCharges’, ‘TotalCharges’ 计算相关系数，其中 ‘TotalCharges’ 与其他两列特征的相关系数均大于0.6，即存在较强相关性，因此可以考虑删除该列，以避免特征冗余。

nu_fea = data[['tenure', 'MonthlyCharges', 'TotalCharges']]    # 选择连续型数值特征计算相关系数
nu_fea = list(nu_fea)    # 特征名列表
pearson_mat = data[nu_fea].corr(method='spearman')    # 计算皮尔逊相关系数矩阵

plt.figure(figsize=(8,8)) # 建立图像
sns.heatmap(pearson_mat, square=True, annot=True, cmap="YlGnBu")    # 用热度图表示相关系数矩阵
plt.show() # 展示热度图

data = data.drop(['TotalCharges'], axis=1)

data.head(10)    # 观察此时的数据集

6、模型预测

6.1 类别不平衡问题处理

在可视化环节中，我们观察到正负样本的比例大概在1:3左右，因此需要对正样本进行升采样或对负样本进行降采样。考虑到本数据集仅有7千多条样本，不适合采用降采样，进行升采样更为合理，本案例采用升采样中较为成熟的SMOTE方法生成更多的正样本。

# SMOTE方法代码如下（代码来自博客 https://blog.csdn.net/Yaphat/article/details/52463304）
import random
from sklearn.neighbors import NearestNeighbors    # k近邻算法

class Smote:
    def __init__(self,samples,N,k):
        self.n_samples,self.n_attrs=samples.shape
        self.N=N
        self.k=k
        self.samples=samples
        self.newindex=0

    def over_sampling(self):
        N=int(self.N)
        self.synthetic = np.zeros((self.n_samples * N, self.n_attrs))
        neighbors=NearestNeighbors(n_neighbors=self.k).fit(self.samples)    # 1.对每个少数类样本均求其在所有少数类样本中的k近邻
        for i in range(len(self.samples)):
            nnarray=neighbors.kneighbors(self.samples[i].reshape(1,-1),return_distance=False)[0]
            self._populate(N,i,nnarray)
        return self.synthetic

    # 2.为每个少数类样本选择k个最近邻中的N个；3.并生成N个合成样本
    def _populate(self,N,i,nnarray):
        for j in range(N):
            nn=random.randint(0,self.k-1)
            dif=self.samples[nnarray[nn]]-self.samples[i]
            gap=random.random()
            self.synthetic[self.newindex]=self.samples[i]+gap*dif
            self.newindex+=1

# 每个正样本用SMOTE方法随机生成两个新的样本
posDf = data[data['Churn'] == 1].drop(['Churn'], axis=1)    # 共1869条正样本, 取其所有特征列
posArray = posDf.values    # pd.DataFrame -> np.array, 以满足SMOTE方法的输入要求
newPosArray = Smote(posArray, 2, 5).over_sampling()
newPosDf = pd.DataFrame(newPosArray)    # np.array -> pd.DataFrame

newPosDf.head(10)    # 观察此时的新样本   

# 调整为正样本在数据集中应有的格式
newPosDf.columns = posDf.columns    # 还原特征名
cateCols = list(newPosDf.columns.drop(['tenure', 'MonthlyCharges']))   # 提取离散特征名组成的列表
for i in cateCols:
    newPosDf[i] = newPosDf[i].apply(lambda x: 1 if x >= 0.5 else 0)    # 将特征值变回0、1二元数值
newPosDf['Churn'] = 1    # 添加目标变量列

newPosDf.head(10)    # 观察此时的新样本

print("原本的正样本有%d条" % posDf.shape[0])
print("原本的负样本有%d条" % (data.shape[0] - posDf.shape[0]))

为保证正负样本平衡，从新生成的样本中取出（5174 - 1869 = 3305）条样本，并加入原数据集进行shuffle操作。

# 构建类别平衡的数据集
from sklearn.utils import shuffle    

newPosDf = newPosDf[:3305]    # 直接选取前3305条样本
data = pd.concat([data, newPosDf])    # 竖向拼接
# data = shuffle(data).reset_index(drop=True)

print("此时数据集的规模为：", data.shape)

6.2 交叉验证

同样考虑到样本数较少的问题，本案例采用K折交叉验证的方式进行预测，提高数据利用率；此外，采用逻辑回归、SVM、随机森林、AdaBoost、XGBoost等算法构建模型，从中选择预测效果较好的模型进行最终的预测。

# K折交叉验证代码
# from sklearn.cross_validation import KFold
from sklearn.model_selection import KFold

def kFold_cv(X, y, classifier, **kwargs):
    """
    :param X: 特征
    :param y: 目标变量
    :param classifier: 分类器
    :param **kwargs: 参数
    :return: 预测结果
    """
    kf = KFold(n_splits=5, shuffle=True) 
    y_pred = np.zeros(len(y))    # 初始化y_pred数组
    
    for train_index, test_index in kf.split(X):  
        X_train = X[train_index]    
        X_test = X[test_index]
        y_train = y[train_index]    # 划分数据集
        clf = classifier(**kwargs)    
        clf.fit(X_train, y_train)    # 模型训练
        y_pred[test_index] = clf.predict(X_test)    # 模型预测
    
    return y_pred  

# 模型预测
from sklearn.linear_model import LogisticRegression as LR    # 逻辑回归
from sklearn.svm import SVC    # SVM
from sklearn.ensemble import RandomForestClassifier as RF    # 随机森林
from sklearn.ensemble import AdaBoostClassifier as Adaboost    # AdaBoost
from xgboost import XGBClassifier as XGB    # XGBoost

# X = data.iloc[:, :-1].as_matrix()
X = data.iloc[:, :-1].iloc[:,:].values # Kagging
y = data.iloc[:, -1].values

# 此处仅做演示，因此未进行调参过程
lr_pred = kFold_cv(X, y, LR)
svc_pred = kFold_cv(X, y, SVC)
rf_pred = kFold_cv(X, y, RF)
ada_pred = kFold_cv(X, y, Adaboost)
xgb_pred = kFold_cv(X, y, XGB)

7、模型评估

对于电信用户流失预测问题，通常更加需要关心的是真正流失的用户，因此我们需要寻找一个能够较好衡量这一现象的评价指标。
在机器学习领域，混淆矩阵（confusion matrix），又称为可能性表格或错误矩阵。它是一种特定的矩阵用来呈现算法性能的可视化效果，通常是有监督学习。观察下面混淆矩阵：

		预测
		1	0	合计
实际	1	True Postive TP	Frue Negative FN	Actual Postive （TP+FN）
	0	False Postive FP	True Negative TN	Actual Negative （FP+TN）
合计		Predicted Postive （TP+FP）	Predicted Negative （FN+TN）	TP+FN+FP+TN

通常会用精确率、召回率等来评价结果，其中，精确率（P）和召回率（R）的定义如下：
&id=eJFtC)

对于本案例：
精确率：在所有我们预测为流失的样本中，真正流失的样本数；
召回率：在真正流失的样本中，我们预测到多少条样本。
很明显，召回率是运营商们主要关心的指标，即宁可把流失的客户预测为流失客户而进行多余的留客行为，也不遗漏任何一名真正流失的客户。
本案例采用精确率、召回率以及综合两者的F1值，但主要的重点还是放在召回率上面。

from sklearn.metrics import precision_score, recall_score, f1_score    # 导入精确率、召回率、F1值等评价指标

scoreDf = pd.DataFrame(columns=['LR', 'SVC', 'RandomForest', 'AdaBoost', 'XGBoost'])
pred = [lr_pred, svc_pred, rf_pred, ada_pred, xgb_pred]
for i in range(5):
    r = recall_score(y, pred[i])
    p = precision_score(y, pred[i])
    f1 = f1_score(y, pred[i])
    scoreDf.iloc[:, i] = pd.Series([r, p, f1])

scoreDf.index = ['Recall', 'Precision', 'F1-score']
scoreDf

由上表能够看出在五种模型当中RandomForest随机森林算法的表现效果是最好的，其次是XGBoost算法。也可以采用召回率最高的RandomForest和XGBoost进行加权平均融合或者Stacking融合。本案例采用RandomForest单模型进行演示。

# 特征重要性
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values

kf = KFold(n_splits=5, shuffle=True, random_state=0)
y_pred = np.zeros(len(y))    # 初始化y_pred数组
clf = RF()

for train_index, test_index in kf.split(X):
    X_train = X[train_index]    
    X_test = X[test_index]
    y_train = y[train_index]    # 划分数据集
    clf.fit(X_train, y_train)    # 模型训练
    y_pred[test_index] = clf.predict(X_test)    # 模型预测
    
feature_importances = pd.DataFrame(clf.feature_importances_,
                                   index = data.columns.drop(['Churn']),
                                    columns=['importance']).sort_values('importance', ascending=False)
feature_importances    # 查看特征重要性

8、分析与决策

8.1 结合用户画像

在可视化阶段能够发现较易流失的客户在各个特征的用户画像如下：

• 基本信息
  • 老年人
  • 未婚
  • 无家属
  • 入网时间段（2个月以内）
• 开通业务
  • 开通光纤业务
  • 未开通在线安全、在线备份、设备保护、技术主持等互联网增值业务签订合约
• 签订合约
  • 合约期限较短
  • 采用电子结算（多为按月支付）
  • 每月费用较高，特别是70~110之间
  • 总费用较低（侧面反应入网时间较短）

根据用户画像，可以从各个方面推出相应活动以求留下可能流失的客户：
1、增加用户的沉没成本（损失厌恶），会员等级、积分制、充值赠送、满减券、其他增值服务。。。
2、培养用户的条件反射（习惯），会员日、定期用户召回、签到、每日定时抽奖、小游戏。。。

• 对老人推出情亲套餐等优惠
• 对未婚、无家属的客户推出暖心套餐等优惠
• 对新入网用户提供一定时期的优惠活动，直到客户达到稳定期
• 提高电话业务、光纤网络、网络电视、网络电影等的客户体验，尝试提高用户的留存率，避免客户流失
• 对能够帮助客户留存的在线安全、在线备份、设备保护、技术支持等互联网增值业务，加大宣传推广的力度
• 对逐月付费用户推出年费优惠活动
• 对使用电子结算、电子支票的客户，推出其他支付方式的优惠活动
• 对美元费用在70~110之间推出一定的优惠活动

。。。

8.1.1 电子账单解锁新权益

现象：“开通电子账单”的人反而容易流失。
基本假设：价格敏感型客户。电子账单，让客户理性消费。
建议：让“电子账单”变成一项“福利。跟连锁便利店，联名发"商品满减券"，每月的账单时间，就将"商品满减券“和账单一起推送过去。文案：您上月消费了XX元，解锁了xx会员权益。
底层规律：增加沉没成本。

8.1.2 “单身用户”尊享亲情网

现象：“单身用户”容易流失。
基本假设：社交欲望较低。
建议：一个单身用户拥有建立3个人以内“亲情网”的权益。
底层规律：增加沉没成本。

8.1.3 每日会员签到

现象：用户对公司粘性较低。
基本假设：除了业务需求外用户很少跟运营商进行接触。
建议：运营商在APP中加入每日签到功能，每日签到都有一定的优惠券或积分，签到满多少天后赠送一定价值的礼品或者福利。
底层规律：培养用户的条件反射。

8.2 结合模型

在模型预测阶段，可以结合预测出的概率值决定对哪些客户进行重点留存：

# 预测客户流失的概率值
def prob_cv(X, y, classifier, **kwargs):
    """
    :param X: 特征
    :param y: 目标变量
    :param classifier: 分类器
    :param **kwargs: 参数
    :return: 预测结果
    """
    kf = KFold(n_splits=5, random_state=0)
    y_pred = np.zeros(len(y))    
    
    for train_index, test_index in kf.split(X):
        X_train = X[train_index]    
        X_test = X[test_index]
        y_train = y[train_index]    
        clf = classifier(**kwargs)    
        clf.fit(X_train, y_train)    
        y_pred[test_index] = clf.predict_proba(X_test)[:,1]    # 注：此处预测的是概率值
    
    return y_pred  

prob = prob_cv(X, y, RF)    # 预测概率值
prob = np.round(prob, 1)    # 对预测出的概率值保留一位小数，便于分组观察

# 合并预测值和真实值
probDf = pd.DataFrame(prob)
churnDf = pd.DataFrame(y)
df1 = pd.concat([probDf, churnDf], axis=1)
df1.columns = ['prob', 'churn']

df1 = df1[:7043]    # 只取原始数据集的7043条样本进行决策
df1.head(10)

# 分组计算每种预测概率值所对应的真实流失率
group = df1.groupby(['prob'])
cnt = group.count() # 每种概率值对应的样本数
true_prob = group.sum() / group.count() #真实流失率
df2 = pd.conact([cnt,true_prob],axis=1).reset_index()
df2.columns = ['prob','cnt','true_prob']

df2

由表可知：预测流失率越大的客户中越有可能真正发生流失。对运营商而言，可以根据各预测概率值分组的真实流失率设定阈值进行决策。例如假设阈值为true_prob = 0.6，即优先关注真正流失为60%以上的群体，也就表示运营商可以对预测结果中大于等于0.9的客户进行重点留存。
学习——DataFountain基于随机森林算法实现电信用户流失预测任务