SAS基本统计分析语句
SAS基本统计分析语句:包含t检验,方差分析,卡方检验,秩和检验,多元线性回归分析,logistic回归分析,广义线性模型,生存分析,判别聚类分析,主成分分析,结构方程模型等。
SAS基本统计分析语句
提示:以下是本篇文章正文内容,数据资料来自第5版医学统计学
一、正态性检验(univariate)
示例: 对样本x 进行正态性检验
data ex; /* 建立数据集 */
input x f @@;
cards;
3.17 2
3.37 3
3.57 9
3.77 14
3.97 22
4.17 30
4.37 21
4.57 15
4.77 10
4.97 6
5.17 4
5.37 2
;
proc univariate data=ex /* 调用univariate过程 */
normal; /* 做正态性检验 */
var x; /* 定义分析变量 */
run;
结果: 小样本量采用Shapiro-Wilk法,Pr<W为检验的显著性概率值,P=0.8757,P>0.05,H0成立,样本x 符合正态分布。

/*Code功能:清除日志、输出结果、ods结果*/
dm ' log; clear; output; clear; odsresult;clear;';
二、t检验(means univariate ttest)
示例(1):配对资料两样本均数比较t检验(H0:x1=x2,H1:x1≠x2; α=0.05)
data ex; /*建立数据集*/
input x1 x2 @@;
d=x1-x2; /*计算两个变量的差值*/
cards;
0.840 0.580
0.591 0.509
0.674 0.500
0.632 0.316
0.687 0.337
0.978 0.517
0.750 0.454
0.730 0.512
1.200 0.997
0.870 0.506
;
/*用MEANS作配对资料两个样本均数比较的t检验*/
proc means t prt;
var d; /*定义分析变量d*/
run;
/*用UNIVARIATE过程作配对资料两样本均数比较的t检验*/
proc univariate data=ex;
var d;
run;
结果:P<0.001,故拒绝H0,接受H1,x1,x2差异有统计学意义。
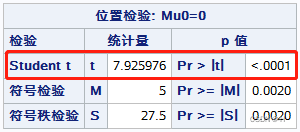
示例(2)独立资料两样本均数比较t检验
data ex; /*建立数据集*/
input x @@;
if _n_<9 then c=1; /*将x变量分为2组*/
else c=2;
cards;
0.66 0.76 0.79 0.88 0.78 0.66 0.75 0.88
0.58 0.69 0.59 0.70 0.69 0.68 0.58 0.60
;
proc ttest;/*调用ttest过程*/
var x; /*定义分析变量*/
class c;/*定义分组变量*/
run;
结果:P<0.05,拒绝H0,两组差异有统计学意义。
三、方差分析
1. 完全随机设计资料的方差分析(anova)
示例:
data ex; /*建立数据集*/
input c x ;/*x为分析变量,c为分组变量*/
cards;
1.00 2.97
1.00 3.30
1.00 4.04
1.00 3.53
1.00 3.56
1.00 3.85
1.00 4.07
1.00 3.52
1.00 3.93
1.00 4.19
1.00 2.96
1.00 2.36
1.00 2.56
1.00 2.52
1.00 2.27
1.00 2.98
1.00 3.72
1.00 2.80
1.00 3.57
1.00 4.02
2.00 1.65
2.00 4.02
2.00 3.53
2.00 3.59
2.00 3.34
2.00 1.66
2.00 4.59
2.00 3.13
2.00 2.64
2.00 2.56
2.00 3.50
2.00 3.25
2.00 3.48
2.00 2.42
2.00 2.41
2.00 2.66
2.00 4.29
2.00 3.70
2.00 3.04
2.00 1.81
3.00 .89
3.00 1.06
3.00 1.08
3.00 1.27
3.00 1.63
3.00 1.89
3.00 1.19
3.00 2.17
3.00 2.28
3.00 1.72
3.00 1.98
3.00 1.74
3.00 2.16
3.00 3.37
3.00 2.97
3.00 1.69
3.00 .94
3.00 2.11
3.00 2.81
3.00 2.52
;
proc anova;
class c;
model x=c;/*定义模型*/
means c/bon; /*用bonferroni法对多组均数两两比较,也可为/regwq(REGWQ 检验),/tukey(4组以上使用)*/
means c/hovtest;/*用Levene法,进行方差齐性检验*/
quit;
结果:H0:3组相同(不成立),H1:3组不全相同(成立),P<0.001。Levene检验:P值>0.05,符合方差齐性。bonferroni:两两比较,P>0.05,差异没有统计学意义。


2. 随机区组设计资料的方差分析(anova)
示例:
data ex;
input x a b @@; /*x为分析变量,a和b为分组变量*/
cards;
3300 1 1
3630 1 2
3800 1 3
3300 1 4
3600 1 5
3550 1 6
3400 1 7
3400 1 8
3700 1 9
3200 1 10
3500 2 1
3500 2 2
3200 2 3
2800 2 4
2900 2 5
3300 2 6
3250 2 7
2700 2 8
3100 2 9
2710 2 10
3260 3 1
2800 3 2
3500 3 3
2800 3 4
3260 3 5
3020 3 6
3200 3 7
2730 3 8
3800 3 9
2560 3 10
;
proc anova;
class a b;
model x=a b; /*定义模型,分析a和b对x的影响*/
means a/regwq;/*用regwq法对变量a的多组均数进行两两比较*/
quit;
结果::区组比较不全相同(成立),P<0.05。REGWQ:两两比较,没有显著差异。
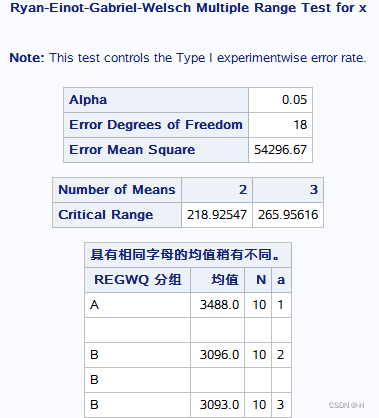
3. 两阶段交叉设计资料的方差分析(anova)
示例:
data ex;
input seq treat time x @@; /*seq为处理顺序变量,treat为处理因素,x为分析变量*/
cards;
1 1 1 760
2 2 1 860
3 1 1 568
4 1 1 780
5 2 1 960
6 2 1 940
7 1 1 635
8 2 1 440
9 1 1 528
10 2 1 800
1 2 2 770
2 1 2 855
3 2 2 602
4 2 2 800
5 1 2 958
6 1 2 952
7 2 2 650
8 1 2 450
9 2 2 530
10 1 2 803
;
proc anova;
class seq time treat;
model x=seq time treat; /*定义模型,分析seq,time和treat对x的影响*/
quit;
结果:
4. 两因素析因设计资料的方差分析(anova)
示例:
data ex;
input x a b @@;/*x为分析变量,a和b为处理因素变量*/
cards;
10.00 1.00 1.00
10.00 1.00 1.00
40.00 1.00 1.00
50.00 1.00 1.00
10.00 1.00 1.00
30.00 1.00 2.00
30.00 1.00 2.00
70.00 1.00 2.00
60.00 1.00 2.00
30.00 1.00 2.00
10.00 2.00 1.00
20.00 2.00 1.00
30.00 2.00 1.00
50.00 2.00 1.00
30.00 2.00 1.00
50.00 2.00 2.00
50.00 2.00 2.00
70.00 2.00 2.00
60.00 2.00 2.00
30.00 2.00 2.00
;
proc anova;
class a b;/*定义分组变量a和b*/
model x=a b a*b; /*定义模型,分析a、b以及ab的交互作用对x的影响*/
quit;
结果: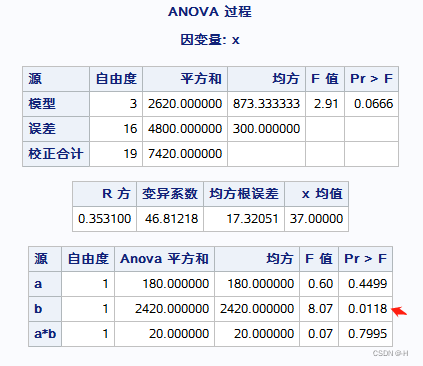
5. 正交设计资料的方差分析(anova)
示例:
data ex;
input x a b c d@@;
cards;
86 1 1 1 1
95 1 1 2 2
91 1 2 1 2
94 1 2 2 1
91 2 1 1 2
96 2 1 2 1
83 2 2 1 1
88 2 2 2 2
;
proc anova;
class a b c d;
model x=a b c d a*b;/*定义模型,分析a、b、c、d以及a和b交互作用对x的影响*/
quit;
结果: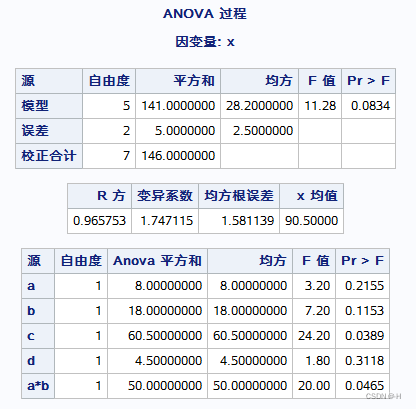
6. 嵌套设计资料的方差分析(glm)
示例:
data ex11_6;
input x a b @@;
cards;
6.91 1 1
6.04 1 1
6.48 1 1
7.08 1 2
6.71 1 2
6.88 1 2
7.41 1 3
7.06 1 3
6.54 1 3
7.33 2 4
7.44 2 4
8.21 2 4
7.33 2 5
7.95 2 5
7.82 2 5
8.78 2 6
8.23 2 6
8.55 2 6
8.35 3 7
8.61 3 7
9.25 3 7
9.11 3 8
8.89 3 8
9.39 3 8
10.14 3 9
9.44 3 9
10.22 3 9
;
proc glm;
class a b;
model x=a a(b);/*定义模型,a为一级处理因素,b为二级处理因素*/
quit;
结果:
7. 重复测量资料的方差分析(glm)
示例:
data ex;
input g t0-t4@@; /*t0-t4分别为5个时间点的分析变量,g为处理因素变量*/
cards;
1 20.69 20.36 20.91 22.99 23.07
1 20.34 19.89 21.43 24.02 24.11
1 20.52 20.41 22.12 23.68 23.24
1 20.86 20.41 22.12 24.02 23.59
1 21.9 21.96 23.5 25.23 24.62
2 20.86 21.79 21.94 24.89 26.52
2 21.03 21.96 22.12 24.54 25.83
2 22.07 23.34 23.32 25.58 27.38
2 20.17 20.52 20.74 23.51 25.49
2 20.34 20.76 21.6 23.51 25.83
3 22.59 21.62 21.94 25.58 25.14
3 22.24 22.33 22.46 27.82 25.66
3 21.21 22.31 22.29 26.96 26.35
3 21.21 21.96 21.6 27.3 24.62
3 21.55 22.48 21.94 26.78 25.31
;
proc glm;
class g;
model t0-t4=g; /*定义模型,分析g对变量t0-t4的影响*/
repeated time 5 /*命名重复因子为time,有5个水平*/
contrast(1) /*以第一时间点为对照点*/
/summary; /*汇总不同时间点与对照时间点比较的结果*/
quit;
结果:


8. 完全随机设计资料的协方差分析(glm)
示例:
data ex;
input g x y;/*x为协变量,y为分析变量,g为分组变量*/
cards;
.00 48.00 3.50
.00 33.00 4.60
.00 51.00 5.80
.00 43.00 5.80
.00 44.00 4.90
.00 63.00 8.70
.00 49.00 3.60
.00 42.00 5.50
.00 40.00 4.90
.00 47.00 5.10
.00 41.00 4.10
.00 41.00 4.60
.00 56.00 5.10
1.00 58.00 7.30
1.00 41.00 4.70
1.00 71.00 8.40
1.00 76.00 8.80
1.00 49.00 5.10
1.00 33.00 4.90
1.00 54.00 6.70
1.00 65.00 6.40
1.00 39.00 6.00
1.00 52.00 7.50
1.00 45.00 6.40
1.00 58.00 6.80
1.00 67.00 9.20
;
proc glm;
class g;
model y=x g;/*定义模型,分析x、g对y的影响*/
quit;
结果:

四、卡方检验
1.四格表资料的χ2检验 (freq)
示例:
data ex;
input id group eff @@;/*group 分组变量,eff观测指标*/
datalines;
1 1 1
2 1 1
3 1 1
4 1 1
5 1 2
6 1 1
7 1 1
8 1 2
9 1 2
10 1 2
11 1 1
12 1 1
13 1 2
14 2 1
15 2 1
16 2 2
17 2 1
18 2 2
19 2 2
20 2 2
21 2 2
22 2 2
23 2 2
24 2 2
25 2 1
26 2 2
27 2 2
28 2 2
29 2 2
30 2 2
31 2 2
32 2 1
33 2 2
34 2 2
35 2 2
36 1 2
37 2 1
38 2 2
;
proc freq;
tables group*eff
/chisq /*进行卡方检验*/
expected norow nopercent; /*输出每个格的理论频数,不输出行百分比和总百分比*/
run;
结果:
配对四格表χ2检验 ,示例:
data ex;
input A B f @@;/*A,B为配对变量,f为相应频数*/
datalines;
1.00 1.00 11.00
1.00 2.00 12.00
2.00 1.00 2.00
2.00 2.00 33.00
;
proc freq;
tables A*B/agree norow nopercent;
weight f; /*定义频数为 f*/
run;
结果:
2.Fisher确切概率法(freq)
示例:
data ex;
input group x freq @@;
datalines;
1.00 1.00 4.00
1.00 2.00 18.00
2.00 1.00 5.00
2.00 2.00 6.00
;
proc freq;
tables group*x/fisher;
weight freq;
run;
结果:
3.行x列表的χ2检验 (双向有序资料)(freq)
示例:
data ex;
input r c f @@;
datalines;
1 1 70
1 2 22
1 3 4
1 4 2
2 1 27
2 2 24
2 3 9
2 4 3
3 1 16
3 2 23
3 3 13
3 4 7
4 1 9
4 2 20
4 3 15
4 4 14
;
proc freq;
weight f;
tables r*c/chisq expected norow nopercent;
run;
结果: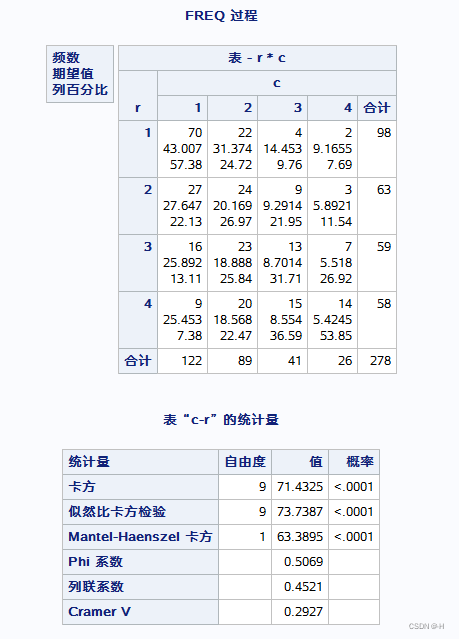
五、秩和检验
1. 配对样本差值的Wilcoxon符号秩检验(univariate)
示例:
data ex;
input x1 x2 @@;
d=x1-x2;
cards;
3.55 2.45
2.00 2.40
3.00 1.80
3.95 3.20
3.80 3.25
3.75 2.70
3.45 2.50
3.05 1.75
;
proc univariate;
var d;
run;
结果: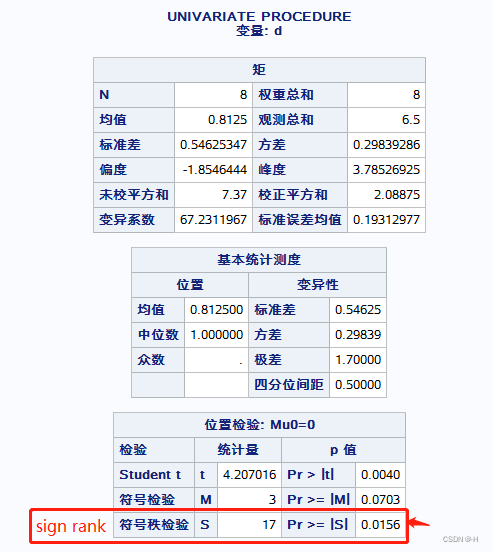
2.两独立样本比较的Wilcoxon秩和检验(npar1way wilcoxon)
示例:
data ex;
input x c @@;
cards;
2.78 1
3.23 1
4.20 1
4.87 1
5.12 1
6.21 1
7.18 1
8.05 1
8.56 1
9.60 1
3.23 2
3.50 2
4.04 2
4.15 2
4.28 2
4.34 2
4.47 2
4.64 2
4.75 2
4.82 2
4.95 2
5.10 2
;
proc npar1way wilcoxon;/*调用nparlway过程,进行Wilcoxon秩和检验*/
var x;
class c;
run;
结果:
2.多组等级资料比较的秩和检验(npar1way wilcoxon)
示例:
data ex;
input c g f @@;
cards;
1 1 49
1 2 31
1 3 5
1 4 15
2 1 45
2 2 9
2 3 22
2 4 4
3 1 15
3 2 28
3 3 11
3 4 20
;
proc npar1way wilcoxon;
var g;/*分析变量*/
class c;/*分组变量*/
freq f;/*频数变量*/
run;
结果:
2.完全随机设计多个样本比较的Kruskal-Wallis检验(npar1way wilcoxon)
示例:
data ex;
input c x @@;
cards;
1 32.5
1 35.5
1 40.5
1 46.0
1 49.0
2 16.0
2 20.5
2 22.5
2 29.0
2 36.0
3 6.5
3 9.0
3 12.5
3 18.0
3 24.0
;
proc npar1way wilcoxon;
var x;
class c;
run;
结果:
2.随机区组设计多个样本比较的Friedman检验(freq)
示例:
data ex;
input x a b @@;/*x为分析变量,a为分组变量,b为区组变量*/
cards;
8.4 1 1 9.6 2 1 9.8 3 1 11.7 4 1
11.6 1 2 12.7 2 2 11.8 3 2 12.0 4 2
9.4 1 3 9.1 2 3 10.4 3 3 9.8 4 3
9.8 1 4 8.7 2 4 9.9 3 4 12.0 4 4
8.3 1 5 8.0 2 5 8.6 3 5 8.6 4 5
8.6 1 6 9.8 2 6 9.6 3 6 10.6 4 6
8.9 1 7 9.0 2 7 10.6 3 7 11.4 4 7
7.8 1 8 8.2 2 8 8.5 3 8 10.8 4 8
;
proc freq;
tables b*a*x /*作列联表*/
/scores=rank /*对x进行排秩*/
cmh2; /*进行friedman检验*/
run;
结果:
六、多元线性回归分析
1. 两变量分析
1.1 直线回归分析(reg)
示例:
data ex;
input x y;
cards;
56 5.32
32 3.21
41 4.67
51 5.03
25 3.01
35 3.57
21 2.98
47 3.93
62 5.62
;
proc reg;
model y=x;/*y为应变量,x为自变量*/
quit;
/*model 添加关键字,可得其他统计量,如:
/stb:标准化偏回归系数
/p:每个观测实际值,预测值,残差
/cli:每个观测 预测值均数的双侧95%CI
/clm:每个观测 预测值的双侧95%CI
*/
结果:
1.2 直线相关分析(corr)
示例:
data ex;
input x y;
cards;
12.81 10.23
11.89 10.01
13.51 11.02
10.82 9.08
14.12 12.89
12.53 11.28
11.94 10.59
11.23 10.88
14.72 12.60
12.45 11.26
11.30 10.02
12.08 11.55
;
proc corr;
var x y;/*相关分析变量*/
run;
结果:
1.3 秩相关分析(corr spearman)
示例:
data ex;
input x y;
cards;
0.03 0.05
0.14 0.34
0.2 0.93
0.43 0.69
0.44 0.38
0.45 0.79
0.47 1.19
0.65 4.74
0.95 2.31
0.96 5.95
2.44 1.11
2.69 3.53
3.07 3.48
7.78 5.65
9.82 33.95
18.93 17.16
22.59 8.42
27.96 9.33
;
proc corr spearman;/*spearman相关分析*/
var x y;
run;
结果:
1.4 对数曲线回归分析(nlin)
示例:
data ex;
input x y;
cards;
0.005 34.11
0.050 57.99
0.500 94.49
5.000 128.50
25.000 169.98
;
proc nlin;
parms a=0 b=0;/*定义初始值*/
model y=a+b*log10(x);/*对数模型:y=应变量,x=自变量*/
quit;
结果:
1.5 指数曲线回归分析(nlin)
示例:
data ex;
input x y;
cards;
2 54
5 50
7 45
10 37
14 35
19 25
26 20
31 16
34 18
38 13
45 8
52 11
53 8
60 4
65 6
;
proc nlin;
parms a=4 b=0.03;/*定义初始值*/
model y=exp(a+b*x);/*指数模型:y=应变量,x=自变量*/
quit;
结果:
2. 多元回归分析(reg)
示例:
data ex;
input x1-x4 y @@;
cards;
5.68 1.90 4.53 8.2 11.2
3.79 1.64 7.32 6.9 8.8
6.02 3.56 6.95 10.8 12.3
4.85 1.07 5.88 8.3 11.6
4.60 2.32 4.05 7.5 13.4
6.05 .64 1.42 13.6 18.3
4.90 8.50 12.60 8.5 11.1
7.08 3.00 6.75 11.5 12.1
3.85 2.11 16.28 7.9 9.6
4.65 .63 6.59 7.1 8.4
4.59 1.97 3.61 8.7 9.3
4.29 1.97 6.61 7.8 10.6
7.97 1.93 7.57 9.9 8.4
6.19 1.18 1.42 6.9 9.6
6.13 2.06 10.35 10.5 10.9
5.71 1.78 8.53 8.0 10.1
6.40 2.40 4.53 10.3 14.8
6.06 3.67 12.79 7.1 9.1
5.09 1.03 2.53 8.9 10.8
6.13 1.71 5.28 9.9 10.2
5.78 3.36 2.96 8.0 13.6
5.43 1.13 4.31 11.3 14.9
6.50 6.21 3.47 12.3 16.0
7.98 7.92 3.37 9.8 13.2
11.54 10.89 1.20 10.5 20.0
5.84 .92 8.61 6.4 13.3
3.84 1.20 6.45 9.6 10.4
;
proc reg;
model y=x1-x4/*x=自变量,y=应变量*/
/*逐步回归添加下方语句*/
/selection=stepwise /*选择逐步回归方法*/
sle=0.10 /*定义入选变量界值*/
sls=0.15;/*定义剔除变量界值*/
;
quit;
手动筛选—结果:
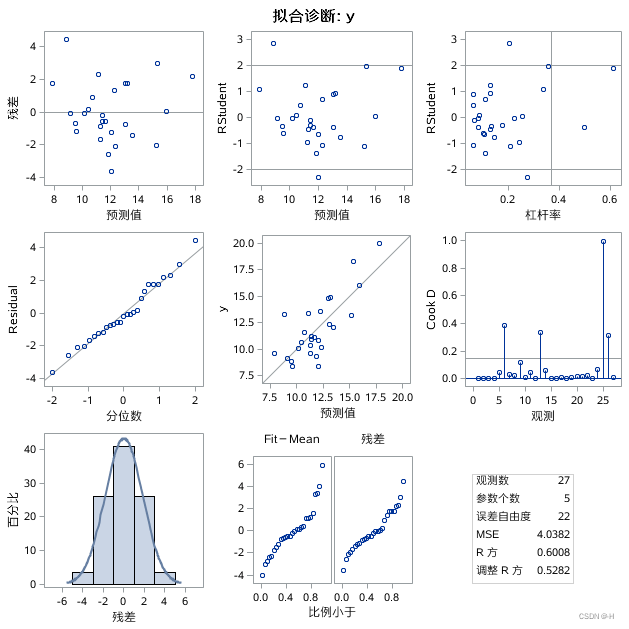
逐步回归—拟合结果:

七、logistic回归分析
1. 多个自变量的logistic回归分析(logistic)
示例:
data ex;
input x1-x8 y @@;
cards;
3 1 0 1 0 0 1 1 0
2 0 1 1 0 0 1 0 0
2 1 0 1 0 0 1 0 0
2 0 0 1 0 0 1 0 0
3 0 0 1 0 1 1 1 0
3 0 1 1 0 0 2 1 0
2 0 1 0 0 0 1 0 0
3 0 1 1 1 0 1 0 0
2 0 0 0 0 0 1 1 0
1 0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1 0
1 0 0 0 0 0 2 1 0
2 0 0 0 0 0 1 0 0
4 1 0 1 0 0 1 0 0
3 0 1 1 0 0 1 1 0
1 0 0 1 0 0 3 1 0
2 0 0 1 0 0 1 0 0
1 0 0 1 0 0 1 1 0
3 1 1 1 1 0 1 0 0
2 1 1 1 1 0 2 0 0
3 1 0 1 0 0 1 0 0
2 1 1 0 1 0 3 1 0
2 0 0 1 1 0 1 1 0
2 0 0 0 0 0 1 0 0
2 0 1 0 0 0 1 0 0
2 0 0 1 1 0 1 1 0
2 0 0 0 0 0 1 0 0
2 0 0 0 0 0 2 1 0
2 1 1 1 0 1 2 1 1
3 0 0 1 1 1 2 1 1
2 0 0 1 1 1 1 0 1
3 1 1 1 1 1 3 1 1
2 0 0 1 0 0 1 1 1
2 0 1 0 1 1 1 1 1
2 0 0 1 0 1 1 0 1
2 1 1 1 1 0 1 1 1
3 1 1 1 1 0 1 1 1
3 1 1 1 0 1 1 1 1
3 1 1 1 1 0 1 1 1
3 0 1 0 0 0 1 0 1
2 1 1 1 1 0 2 1 1
3 1 0 1 0 1 2 1 1
3 1 0 1 0 0 1 1 1
3 1 1 1 1 1 2 0 1
4 0 0 1 1 0 3 1 1
3 1 1 1 1 0 3 1 1
4 1 1 1 1 0 3 0 1
3 0 1 1 1 0 1 1 1
4 0 0 1 0 0 2 1 1
1 0 1 1 1 0 2 1 1
2 0 1 1 0 1 2 1 1
2 1 1 1 0 0 2 1 1
2 1 0 1 0 0 1 1 1
3 1 1 0 1 0 3 1 1
;
proc logistic decending;/*decending为y降序排列*/
model y=x1-x8;
quit;
结果: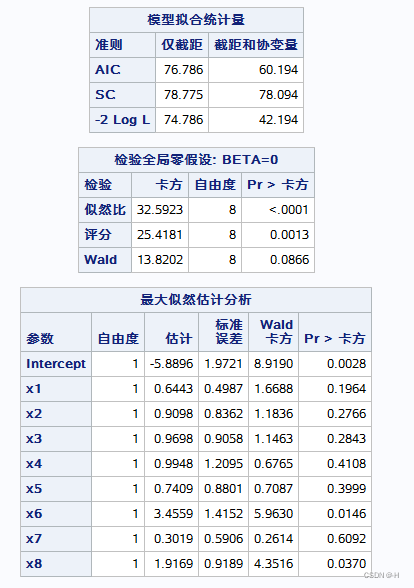

2. 1:M配对资料的logistic回归分析(phreg)
示例:
data ex;
input i y x1-x6 @@; /*i=区组变量,y=患者情况(1=实验组/0=对照组),x1-x6=危险因素*/
t=2-y; /*t=时间变量*/
cards;
1 1 3 5 1 1 1 0
1 0 1 1 1 3 3 0
1 0 1 1 1 3 3 0
2 1 1 3 1 1 3 0
2 0 1 1 1 3 2 0
2 0 1 2 1 3 2 0
3 1 1 4 1 3 2 0
3 0 1 5 1 3 2 0
3 0 1 4 1 3 2 0
4 1 1 4 1 2 1 1
4 0 1 1 1 3 3 0
4 0 2 1 1 3 2 0
5 1 2 4 2 3 2 0
5 0 1 2 1 3 3 0
5 0 2 3 1 3 2 0
6 1 1 3 1 3 2 1
6 0 1 2 1 3 2 0
6 0 1 3 2 3 3 0
7 1 2 1 1 3 2 1
7 0 1 1 1 3 3 0
7 0 1 1 1 3 3 0
8 1 1 2 3 2 2 0
8 0 1 5 1 3 2 0
8 0 1 2 1 3 1 0
9 1 3 4 3 3 2 0
9 0 1 1 1 3 3 0
9 0 1 4 1 3 1 0
10 1 1 4 1 3 3 1
10 0 1 4 1 3 3 0
10 0 1 2 1 3 1 0
11 1 3 4 1 3 2 0
11 0 3 4 1 3 1 0
11 0 1 5 1 3 1 0
12 1 1 4 3 3 3 0
12 0 1 5 1 3 2 0
12 0 1 5 1 3 3 0
13 1 1 4 1 3 2 0
13 0 1 1 1 3 1 0
13 0 1 1 1 3 2 0
14 1 1 3 1 3 2 1
14 0 1 1 1 3 1 0
14 0 1 2 1 3 3 0
15 1 1 4 1 3 2 0
15 0 1 5 1 3 3 0
15 0 1 5 1 3 3 0
16 1 1 4 2 3 1 0
16 0 2 1 1 3 3 0
16 0 1 1 3 3 2 0
17 1 2 3 1 3 2 0
17 0 1 1 2 3 2 0
17 0 1 2 1 3 2 0
18 1 1 4 1 3 2 0
18 0 1 1 1 2 1 0
18 0 1 2 1 3 2 0
19 1 1 3 2 2 2 0
19 0 1 1 1 2 1 0
19 0 2 2 2 3 1 0
20 1 1 4 2 3 2 1
20 0 1 5 1 3 3 0
20 0 1 4 1 3 2 0
21 1 1 5 1 2 1 0
21 0 1 4 1 3 2 0
21 0 1 2 1 3 2 1
22 1 1 2 2 3 1 0
22 0 1 2 1 3 2 0
22 0 1 1 1 3 3 0
23 1 1 3 1 2 2 0
23 0 1 1 1 3 1 1
23 0 1 1 2 3 2 1
24 1 1 2 2 3 2 1
24 0 1 1 1 3 2 0
24 0 1 1 2 3 2 0
25 1 1 4 1 1 1 1
25 0 1 1 1 3 2 0
25 0 1 1 1 3 3 0
;
proc phreg;
model t*y(0)=x1-x6;
strata i; /*定义区组变量*/
quit;
结果:

3. 应变量为有序资料的logistic回归分析(logistic)
示例:
data ex;
input x1 x2 y f;
cards;
1 1 1 9
1 2 1 18
1 2 2 1
1 3 1 15
1 3 2 8
2 1 2 3
2 2 1 2
2 2 2 15
2 2 3 2
2 3 2 14
2 3 3 4
3 1 2 1
3 2 2 2
3 2 3 12
3 3 3 23
;
run;
proc logistic descending;
freq f;
model y=x1 x2;
quit;
结果:

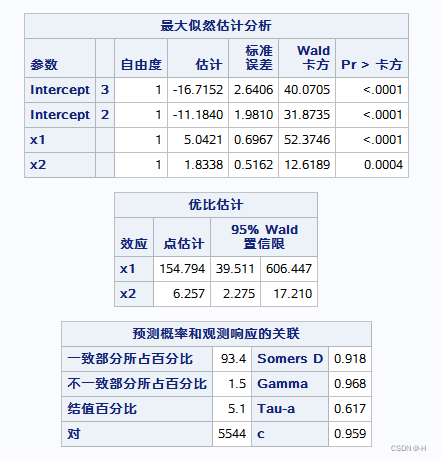
4. 应变量为多分类资料的logistic回归分析(logistic)
示例:
data ex;
input x1 x2 y f;/*y为多分类资料,x1-2为自变量,f为发生频数*/
cards;
1 1 1 9
1 2 1 18
1 2 2 1
1 3 1 15
1 3 2 8
2 1 2 3
2 2 1 2
2 2 2 15
2 2 3 2
2 3 2 14
2 3 3 4
3 1 2 1
3 2 2 2
3 2 3 12
3 3 3 23
;
run;
proc logistic;
freq f; /*定义频数变量为f*/
model y(ref='1')/*ref语句指明,对照组为y=1*/
=x1 x2
/link=glogit;/*指定多分类 应变量 回归模型*/
quit;
结果:


八、广义线性模型
1.对数线性模型(genmod)
示例:
data ex;
input x y count;
cards;
1 1 86
1 2 81
2 1 38
2 2 43
3 1 49
3 2 49
;
proc genmod data=ex order=data;;
class x y; /*定义分组变量*/
model count = x y x*y /*定义模型,count为应变量,x、y及xy交互为自变量*/
/link=log /*定义连接函数为对数log*/
dist= poi /*定义内部概率分布为泊松分布*/
obstats /*打印附加统计量表*/
residuals; /*将Pearson、偏差、似然残差加至附加统计量表中*/
run;
结果:


2.Poisson模型(genmod)
示例:
data ex;
Input agegr$ x n y @@; /*x为有无暴露,n为观察年数,y为死亡人数*/
x1=(x='1'); /*以无暴露x=1为对照,设置有暴露的哑变量x1*/
x2=(agegr='50-59'); /*以年龄40-49岁为对照,设置年龄50-59的哑变量x2*/
x3=(agegr='60-69'); /*以年龄40-49岁为对照,设置年龄60-69的哑变量x3*/
x4=(agegr='>=70');
lg=log(n); /*观察年数取对数*/
cards;
40-49 0 38336.7 14
40-49 1 11026.1 7
50-59 0 31019.1 38
50-59 1 10792.1 42
60-69 0 17495.5 58
60-69 1 6897.9 59
>=70 0 6842.4 41
>=70 1 2580.9 17
;
proc genmod;
model y=x1 x2-x4
/link=log /*定义连接函数为对数log*/
DIST=poisson /*定义内部概率分布为poisson分布*/
offset=lg /*设置偏移量*/
LRCI /*计算参数双侧CI*/
scale=DEVIANCE; /*设置尺度参数*/
run;
结果:

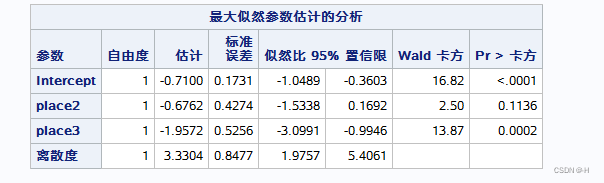
3.负二项模型(genmod)
示例:
data ex;
Input place$ outcome f @@;/*place=居住地,f=频数*/
place2=(place='slum'); /*以农村为对照,设置城市的哑变量*/
place3=(place='urban'); /*以农村为对照,设置平民区的哑变量*/
cards;
rural 0 136
rural 1 23
rural 2 10
rural 3 5
rural 4 2
rural 5 1
rural 6 1
rural 11 1
slum 0 38
slum 1 8
slum 2 2
urban 0 67
urban 1 5
;
proc genmod;
freq f;
model outcome=place2-place3 /*定义模型:outout=应变量,plece2-3=自变量*/
/link=log /*定义连接函数为对数log量*/
DIST=nb /*定义内部概率分布为负二项分布*/
LRCI ; /*计算参数双侧CI*/
run;
结果:

九、生存分析
1.Log-rank检验(lifetest)
示例:
data ex18_4;
input t d g @@;/*t=时间变量,d=截尾变量,g=分组变量*/
cards;
1 1 1
3 1 1
5 1 1
5 1 1
5 1 1
6 1 1
6 1 1
6 1 1
7 1 1
8 1 1
10 1 1
10 1 1
14 0 1
17 1 1
19 0 1
20 0 1
22 0 1
26 0 1
31 0 1
34 1 1
34 0 1
44 1 1
59 1 1
1 1 2
1 1 2
2 1 2
3 1 2
3 1 2
4 1 2
4 1 2
4 1 2
6 1 2
6 1 2
8 1 2
9 1 2
9 1 2
10 1 2
11 1 2
12 1 2
13 1 2
15 1 2
17 1 2
18 1 2
;
proc lifetest plots=(s);/*调用lifetest 制作生存曲线*/
time t*d(0); /*变量值为0表示结尾数据*/
strata g; /*定义g为分组变量*/
run;
结果:

2.Cox回归分析(phreg)
示例:
data ex;
input x1-x6 t y@@;/*x1-x6为危险因素变量,t=时间变量,y=截尾变量*/
cards;
54 0 0 1 1 0 52 0
57 0 1 0 0 0 51 0
58 0 0 0 1 1 35 1
43 1 1 1 1 0 103 0
48 0 1 0 0 0 7 1
40 0 1 0 0 0 60 0
44 0 1 0 0 0 58 0
36 0 0 0 1 1 29 1
39 1 1 1 0 1 70 0
42 0 1 0 0 1 67 0
42 0 1 0 0 0 66 0
42 1 0 1 1 0 87 0
51 1 1 1 0 0 85 0
55 0 1 0 0 1 82 0
49 1 1 1 0 1 76 0
52 1 1 1 0 1 74 0
48 1 1 1 0 0 63 0
54 1 0 1 1 1 101 0
38 0 1 0 0 0 100 0
40 1 1 1 0 1 66 1
38 0 0 0 1 0 93 0
19 0 0 0 1 0 24 1
67 1 0 1 1 0 93 0
37 0 0 1 1 0 90 0
43 1 0 0 1 0 15 1
49 0 0 0 1 0 3 1
50 1 1 1 1 1 87 0
53 1 1 1 0 0 120 0
32 1 1 1 0 0 120 0
46 0 1 0 0 1 120 0
43 1 0 1 1 0 120 0
44 1 0 1 1 0 120 0
62 0 0 0 1 0 120 0
40 1 1 1 0 1 40 1
50 1 0 0 1 0 26 1
33 1 1 0 0 0 120 0
57 1 1 1 0 0 120 0
48 1 0 0 1 0 120 0
28 0 0 0 1 0 3 1
54 1 0 1 1 0 120 1
35 0 1 0 1 1 7 1
47 0 0 0 1 0 18 1
49 1 0 1 1 0 120 0
43 0 1 0 0 0 120 0
48 1 1 0 0 0 15 1
44 0 0 0 1 0 4 1
60 1 1 1 0 0 120 0
40 0 0 0 1 0 16 1
32 0 1 0 0 1 24 1
44 0 0 0 1 1 19 1
48 1 0 0 1 0 120 0
72 0 1 0 1 0 24 1
42 0 0 0 1 0 2 1
63 1 0 1 1 0 120 0
55 0 1 1 0 0 12 1
39 0 0 0 1 0 5 1
44 0 0 0 1 0 120 0
42 1 1 1 0 0 120 0
74 0 0 0 1 1 7 1
61 0 1 0 1 0 40 1
45 1 0 1 1 0 108 0
38 0 1 0 0 0 24 1
62 0 0 0 1 0 16 1
;
proc phreg;
class x2-x6 /*定义分组变量x2-x6*/
/ref=first; /*ref语句指明,对照组为第一类*/
model t*y(0)=x1-x6; /*定义模型,变量值0表示截尾数据*/
quit;
结果:


十、判别和聚类分析
1.判别分析(discrim)
示例:
data ex;
input g x1-x4;/*g为分组变量,x1-x4用于进行判别分析的指标*/
cards;
1 16 0.88 51 0
1 16 0.62 53 2
1 20 1.03 48 6
1 22 0.82 54 0
1 24 0.97 54 0
1 32 0.79 52 9
1 20 0.85 54 0
1 25 0.71 58 12
1 17 0.54 55 6
1 15 1.03 50 0
1 29 0.48 53 2
1 24 1.01 54 0
1 17 0.85 51 0
1 20 0.78 52 2
1 20 0.7 54 5
1 21 0.97 50 1
1 21 0.51 52 0
1 22 0.68 52 0
1 19 0.71 53 0
1 18 0.67 54 1
1 20 1.04 49 0
1 20 0.52 51 0
1 16 1.03 51 3
1 19 1.51 50 2
1 17 0.71 54 11
1 16 1.07 52 7
1 19 1.03 54 2
1 21 0.66 52 4
1 20 1.08 51 6
1 19 0.75 54 2
1 16 0.5 52 14
1 25 0.82 51 0
1 20 0.95 51 0
1 20 0.73 50 0
1 22 0.91 53 0
1 18 0.8 53 0
1 16 2.94 51 0
1 19 0.64 50 0
1 20 0.93 55 6
1 24 0.44 54 7
2 11 1.48 58 29
2 10 0.92 54 20
2 8 0.94 55 51
2 16 0.82 57 43
2 12 0.7 60 95
2 12 0.92 59 28
2 17 1.59 63 57
2 5 0.44 58 25
2 10 1.59 59 22
2 14 1.28 59 25
2 7 1.34 60 27
2 12 1.94 57 2
2 16 0.89 52 56
2 21 1.23 57 55
2 12 0.78 52 47
2 11 0.55 56 67
2 23 1.62 58 49
2 12 1.65 61 10
2 16 1.52 55 7
2 8 0.35 52 25
2 13 1.28 55 54
2 10 0.9 54 57
2 8 0.65 59 35
2 18 1.73 54 93
2 14 0.95 55 35
2 12 1.14 56 31
2 8 1.76 56 54
3 6 0.75 51 28
3 12 0.44 57 56
3 10 0.39 59 43
3 10 1.25 51 7
3 6 0.7 55 37
3 12 0.71 54 39
3 6 1.25 58 42
3 11 1.37 59 42
3 5 1.09 62 95
3 17 1 55 28
3 8 1.3 50 77
3 15 0.7 56 30
3 10 0.49 56 38
3 12 0.97 51 27
3 10 0.58 58 2
3 14 0.83 55 60
3 4 0.54 58 105
3 17 0.85 49 39
;
proc discrim;
class g;
var x1-x4; /*定义用于判别分析的指标变量*/
run;
结果:
2.聚类分析(cluster-Ward varclus)
示例:
data ex;
input region $ x1-x7;/*region为对象(样品),x1-x7为指标*/
cards;
北京 5.56 0.09 10.35 82.44 10.08 11.33 15.10
天津 4.39 0.08 7.80 78.10 10.06 6.48 10.20
河北 5.25 0.15 5.75 83.72 8.79 5.66 15.60
山西 5.34 0.14 3.64 77.58 10.44 6.30 12.30
内蒙古 5.94 0.13 4.13 74.71 9.82 7.13 14.40
辽宁 6.83 0.13 4.59 81.98 10.47 6.66 16.80
吉林 5.66 0.10 3.99 77.59 9.38 6.18 14.10
黑龙江 6.38 0.40 3.11 78.93 10.45 6.05 16.00
上海 5.57 0.11 10.99 95.43 10.13 7.73 16.20
江苏 5.84 0.04 7.28 87.45 9.50 6.82 17.70
浙江 5.54 0.03 10.52 89.36 9.80 8.13 16.80
安徽 4.89 0.07 4.48 86.20 8.68 5.01 15.90
福建 4.66 0.03 5.79 83.09 8.63 5.92 14.10
江西 5.06 0.04 4.67 85.79 8.86 5.10 17.90
山东 5.84 0.16 6.44 83.41 8.63 6.88 18.20
河南 5.85 0.09 6.12 88.39 9.64 6.08 18.30
湖北 6.37 0.06 6.03 92.71 9.51 6.77 21.70
湖南 6.59 0.03 3.94 85.22 9.06 6.06 21.50
广东 4.41 0.03 7.49 84.03 8.69 6.33 14.60
广西 4.94 0.03 5.34 87.66 8.63 6.25 18.40
海南 4.53 0.03 5.36 81.09 8.88 6.52 12.60
重庆 6.71 0.08 5.06 84.13 9.31 6.23 22.30
四川 6.79 0.07 5.85 91.34 10.45 6.39 22.00
贵州 6.51 0.05 4.26 79.93 8.15 6.31 20.50
云南 5.72 0.04 5.30 83.19 8.51 5.91 18.60
西藏 4.78 0.05 4.75 72.09 8.72 4.90 9.90
陕西 6.29 0.08 4.99 83.67 9.05 8.09 19.60
甘肃 5.58 0.11 5.12 81.55 8.81 5.59 16.70
青海 6.41 0.18 4.26 70.64 8.98 6.98 16.30
宁夏 5.84 0.13 5.88 80.81 8.91 7.29 17.20
新疆 6.85 0.14 4.60 85.01 8.47 7.12 22.40
;
run;
/*对样品聚类*/
proc cluster method=Ward /*采用Ward离差平方和法进行聚类分析*/
standard /*采用对原始指标进行标准化*/
data=ex;
var x1-x7; /*定义指标变量为x1-x7*/
id region; /*定义对象的标识为region*/
run;
proc tree; /*调用tree过程输出聚类图*/
id region;
run;
/*对指标聚类*/
proc varclus data=ex;
var x1-x7;
run;
结果:
…
十一、主成分分析与因子分析
1.主成分分析(princomp)
示例:
data ex;
input no x1-x9;
cards;
1 3.68 5.07 1.90 3.66 8.82 1.71 4.42 4.12 2.24
2 4.30 6.58 2.85 4.50 10.60 2.10 5.81 5.10 2.81
3 4.80 6.66 2.52 4.13 8.96 2.44 5.03 4.77 3.21
4 4.16 6.52 2.29 3.93 8.61 2.06 4.29 4.11 2.61
5 6.14 10.70 3.58 8.34 23.60 2.29 12.10 8.85 2.91
6 3.87 5.85 2.07 3.93 9.56 1.87 5.20 4.47 2.38
7 3.91 6.20 2.31 4.00 10.10 1.90 5.39 4.80 2.49
8 3.37 5.52 1.86 3.75 9.45 1.58 5.00 4.03 1.94
9 5.99 10.30 3.58 8.08 23.30 2.24 11.90 8.75 2.94
10 2.37 4.12 1.27 3.14 8.98 0.96 4.66 3.46 1.13
11 2.99 5.20 1.77 3.76 10.00 1.32 5.31 3.97 1.52
12 3.65 5.22 2.05 3.37 8.25 1.73 3.99 4.05 2.38
13 4.06 6.47 2.29 3.92 8.41 2.00 4.61 4.05 2.52
14 4.53 6.42 2.45 3.86 7.97 2.24 4.54 4.30 3.05
15 4.11 6.64 2.34 4.53 10.60 2.00 5.79 4.68 2.46
16 3.96 6.05 2.18 3.55 7.98 1.95 4.52 4.02 2.53
17 3.69 6.14 2.16 3.41 7.24 1.84 4.08 3.47 2.22
18 3.58 5.77 1.95 3.09 6.56 1.82 3.75 3.36 2.27
19 6.18 10.90 3.84 8.24 24.00 2.32 12.20 8.97 2.97
20 4.59 7.21 2.44 4.19 8.76 2.34 5.00 4.48 3.05
21 3.94 6.26 2.16 3.71 8.01 1.95 4.53 3.89 2.43
22 3.98 6.70 2.30 4.37 10.40 1.87 5.73 4.50 2.30
23 6.61 10.90 4.05 6.45 12.00 3.44 6.69 5.88 4.10
24 4.54 6.47 2.38 4.10 9.26 2.27 5.17 4.74 3.01
25 4.30 6.94 2.32 4.26 10.20 2.04 5.58 4.79 2.68
26 5.37 8.73 3.16 4.56 7.59 2.88 4.63 4.44 3.64
27 3.86 6.15 2.16 3.36 7.12 1.95 4.09 3.60 2.45
28 6.13 10.80 3.81 8.30 24.10 2.30 12.30 8.98 2.90
29 4.11 6.84 2.32 4.60 11.10 1.95 5.91 4.78 2.34
30 3.52 5.57 2.00 2.90 5.98 1.79 3.44 3.15 2.21
31 3.81 6.02 2.18 3.45 7.19 1.88 4.14 3.65 2.45
32 5.24 8.76 3.16 4.86 9.51 2.73 5.36 4.76 3.34
33 4.38 7.03 2.36 4.50 10.50 2.13 5.79 4.83 2.66
34 4.76 8.27 3.03 5.36 12.10 2.33 6.58 5.26 2.84
35 4.64 6.71 2.71 4.01 8.02 2.39 4.57 4.36 3.16
36 4.62 8.86 2.92 6.38 19.20 1.00 9.63 7.31 2.28
37 4.10 6.64 2.22 4.25 9.98 1.96 5.44 4.54 2.49
38 3.68 5.92 1.70 3.91 9.58 1.68 5.17 4.22 2.09
39 4.49 8.59 2.86 5.84 17.20 1.73 8.79 6.87 2.46
;
proc princomp;
var x1-x9;
run;
结果:


2.因子分析(factor)
示例:
data ex;
input x1-x9;
cards;
4.34 389 99.06 1.23 25.46 93.15 3.56 97.51 61.66
3.45 271 88.28 .85 23.55 94.31 2.44 97.94 73.33
4.38 385 103.97 1.21 26.54 92.53 4.02 98.48 76.79
4.18 377 99.48 1.19 26.89 93.86 2.92 99.41 63.16
4.32 378 102.01 1.19 27.63 93.18 1.99 99.71 80.00
4.13 349 97.55 1.10 27.34 90.63 4.38 99.03 63.16
4.57 361 91.66 1.14 24.89 90.60 2.73 99.69 73.53
4.31 209 62.18 .52 31.74 91.67 3.65 99.48 61.11
4.06 425 83.27 .93 26.56 93.81 3.09 99.48 70.73
4.43 458 92.39 .95 24.26 91.12 4.21 99.76 79.07
4.13 496 95.43 1.03 28.75 93.43 3.50 99.10 80.49
4.10 514 92.99 1.07 26.31 93.24 4.22 100.00 78.95
4.11 490 80.90 .97 26.90 93.68 4.97 99.77 80.53
3.53 344 79.66 .68 31.87 94.77 3.59 100.00 81.97
4.16 508 90.98 1.01 29.43 95.75 2.77 98.72 62.86
4.17 545 92.98 1.08 26.92 94.89 3.14 99.41 82.35
4.16 507 95.10 1.01 25.82 94.41 2.80 99.35 60.61
4.86 540 93.17 1.07 27.59 93.47 2.77 99.80 70.21
5.06 552 84.38 1.10 27.56 95.15 3.10 98.63 69.23
4.03 453 72.69 .90 26.03 91.94 4.50 99.05 60.42
4.15 529 86.53 1.05 22.40 91.52 3.84 98.58 68.42
3.94 515 91.01 1.02 25.44 94.88 2.56 99.36 73.91
4.12 552 89.14 1.10 25.70 92.65 3.87 95.52 66.67
4.42 597 90.18 1.18 26.94 93.03 3.76 99.28 73.81
3.05 437 78.81 .87 23.05 94.46 4.03 96.22 87.10
3.94 477 87.34 .95 26.78 91.78 4.57 94.28 87.34
4.14 638 88.57 1.27 26.53 95.16 1.67 94.50 91.67
3.87 583 89.82 1.16 22.66 93.43 3.55 94.49 89.07
4.08 552 90.19 1.10 22.53 90.36 3.47 97.88 87.14
4.14 551 90.81 1.09 23.06 91.65 2.47 97.72 87.13
4.04 574 81.36 1.14 26.65 93.74 1.61 98.20 93.02
3.93 515 76.87 1.02 23.88 93.82 3.09 95.46 88.37
3.90 555 80.58 1.10 23.08 94.38 2.06 96.82 91.79
3.62 554 87.21 1.10 22.50 92.43 3.22 97.16 87.77
3.75 586 90.31 1.12 23.73 92.47 2.07 97.74 93.89
3.77 627 86.47 1.24 23.22 91.17 3.40 98.98 89.80
;
proc factor;
run;
结果:

十二、典型相关分析和结构方程模型
1. 典型相关分析(cancorr)
示例:
data ex22_1;
input x1-x3 y1-y2;
cards;
2 14 16 11 70
6 2 10 12 58
6 6 8 16 60
0 0 0 24 77
4 4 8 8 69
4 8 10 19 77
2 2 6 17 64
10 6 12 17 74
4 2 6 11 59
4 6 14 20 62
2 8 6 13 58
2 2 2 14 79
10 2 8 14 57
0 0 0 13 72
2 4 6 14 70
0 6 2 20 70
0 4 2 21 69
0 12 4 13 68
0 0 0 24 80
0 2 0 27 83
0 0 2 20 75
2 10 10 23 67
2 4 8 8 65
4 0 2 21 66
2 2 2 17 71
12 12 12 16 57
2 2 8 16 60
12 4 8 21 61
16 10 18 10 58
0 2 4 17 73
0 0 0 20 70
6 10 12 9 59
0 2 2 17 75
0 0 0 16 78
14 14 14 12 66
12 16 12 10 42
6 6 8 8 63
4 2 2 23 71
18 14 18 20 62
12 4 14 9 56
0 0 0 17 73
0 0 0 22 78
2 6 10 20 79
4 4 6 14 69
0 6 2 16 72
8 8 12 12 73
6 10 10 10 73
0 0 2 18 79
4 2 10 21 71
4 4 8 18 75
4 8 14 16 70
0 2 4 16 71
10 8 8 15 68
4 6 8 13 66
6 4 8 13 69
20 24 30 14 44
8 4 16 12 40
4 4 12 17 64
6 18 18 16 55
4 8 6 17 66
0 0 0 18 69
0 2 2 18 63
10 10 12 21 65
0 0 2 16 70
18 24 26 15 44
0 2 6 24 85
0 2 6 18 73
6 2 6 23 75
2 0 4 14 76
18 32 28 9 49
0 0 0 18 77
0 0 0 20 66
2 4 8 17 71
6 6 8 15 64
10 10 14 18 61
0 2 6 18 66
0 2 6 21 74
4 6 10 24 69
4 4 0 15 64
2 2 2 18 74
0 4 6 18 81
0 0 0 28 98
4 4 14 18 62
4 4 8 16 70
6 8 14 12 75
2 4 4 12 65
2 8 10 18 66
14 8 20 9 41
2 0 10 12 52
2 4 6 15 61
4 0 8 23 66
0 2 4 9 72
6 2 6 17 68
2 2 2 25 61
4 2 0 23 69
14 4 10 9 58
0 0 0 15 77
0 4 12 23 77
14 12 18 16 59
0 0 0 12 71
4 4 4 18 64
2 6 6 10 69
2 4 8 20 75
0 4 8 16 70
2 10 6 17 59
14 14 14 5 51
8 4 6 16 63
0 0 6 18 63
12 20 26 19 41
6 6 2 18 70
6 8 12 19 71
0 2 4 19 66
0 2 2 16 75
2 6 0 23 79
8 0 12 10 54
0 8 8 17 71
2 6 0 21 74
8 12 14 20 72
42 42 42 4 26
8 16 10 18 65
0 6 4 19 66
2 4 2 18 71
4 2 12 23 67
2 4 4 21 70
6 4 14 15 60
0 0 4 21 80
4 4 4 23 76
0 0 0 20 69
0 0 0 20 72
4 6 8 22 72
2 2 2 15 67
26 18 22 14 49
2 8 12 14 65
30 20 28 5 46
2 2 6 24 84
4 2 6 20 70
2 0 0 16 59
6 6 4 14 62
14 18 16 7 52
0 2 4 16 75
10 16 16 8 43
0 4 6 21 84
10 12 12 11 49
12 8 10 14 56
10 8 4 18 58
2 2 2 15 72
0 4 6 13 81
0 0 0 20 75
0 0 4 16 72
2 0 4 21 73
8 6 12 20 62
4 4 8 19 67
0 2 4 17 68
16 16 26 7 40
0 2 0 13 67
2 8 10 21 82
2 2 10 18 73
12 12 12 12 60
2 6 4 20 77
2 2 4 16 67
4 8 4 14 69
4 6 6 16 62
2 2 6 16 73
10 12 16 11 59
2 6 8 15 67
2 4 10 15 63
0 0 0 10 69
4 4 10 15 68
4 4 2 24 78
0 2 4 20 78
14 12 18 12 51
10 6 10 14 55
6 8 10 23 62
6 10 12 11 55
0 0 0 19 78
22 8 12 12 55
2 0 6 15 59
0 0 4 22 68
0 2 2 16 61
0 0 2 18 77
0 0 2 19 71
0 2 2 18 77
2 6 10 22 75
2 2 2 22 67
0 2 2 22 76
2 2 2 19 78
0 0 2 20 71
4 8 6 12 56
8 4 12 11 44
12 6 10 15 60
8 10 10 24 64
0 2 0 20 62
0 0 0 20 80
4 8 6 17 65
4 6 10 18 60
0 0 0 24 82
14 18 22 8 46
2 2 2 20 84
2 2 4 12 63
0 0 4 17 77
0 0 0 20 79
0 2 2 21 88
2 0 2 15 68
0 0 0 22 73
0 0 2 17 67
2 8 8 17 66
8 4 8 15 64
0 4 2 23 74
2 2 2 11 76
4 4 4 22 74
14 14 16 16 52
4 2 4 17 77
8 8 12 18 60
4 6 10 18 59
0 0 0 22 80
2 10 6 23 68
6 6 10 10 69
0 2 2 15 71
20 12 20 8 40
4 0 2 17 64
4 12 14 19 62
2 0 6 16 66
6 8 10 19 60
0 0 6 22 77
0 0 0 24 80
0 0 0 17 85
8 6 14 20 70
8 6 12 8 45
2 2 0 22 76
42 42 42 28 50
8 14 14 12 54
0 0 2 17 69
12 14 12 13 61
2 0 0 23 80
0 0 0 16 74
2 4 2 14 72
10 10 10 19 63
8 6 16 6 58
2 4 4 23 79
0 2 2 23 80
2 4 4 17 72
2 10 14 13 53
0 0 0 11 60
34 32 36 11 46
0 0 2 17 65
2 2 4 18 71
2 8 8 22 67
0 8 10 15 68
0 6 10 19 63
0 2 2 22 72
0 2 4 24 79
0 0 2 16 74
6 6 4 15 58
0 0 2 15 71
0 4 4 17 73
20 12 14 12 49
2 4 2 20 60
0 2 2 17 77
2 2 0 10 66
6 6 10 5 56
2 0 4 18 70
2 4 6 26 70
0 4 6 16 67
0 2 6 16 68
4 4 8 13 64
2 6 8 24 80
4 8 10 23 68
0 6 4 21 69
14 6 20 13 53
8 6 8 16 63
2 2 4 16 71
10 8 10 16 71
2 4 4 16 78
6 4 8 13 67
2 6 6 5 60
10 4 10 12 48
8 8 6 22 74
0 0 0 11 68
6 6 8 20 78
6 8 14 15 62
10 8 6 17 62
24 20 24 7 37
0 0 0 16 80
2 4 8 20 77
8 14 10 24 62
12 14 12 16 65
0 0 0 21 81
18 12 20 16 54
0 0 0 16 56
0 2 2 24 87
12 0 8 13 58
0 0 0 20 75
0 2 2 17 72
2 4 4 14 72
0 2 2 23 73
12 10 10 12 63
4 6 8 19 74
4 6 6 14 77
8 6 14 16 65
2 6 2 17 62
12 12 12 18 67
0 8 8 19 73
2 0 4 18 76
14 6 14 14 66
0 0 0 24 86
0 0 2 16 76
6 0 10 16 61
4 6 14 14 66
0 0 6 17 72
4 6 8 16 61
8 6 8 12 66
0 0 0 22 82
0 2 6 11 59
4 12 8 19 67
2 8 4 16 72
0 0 0 19 82
6 14 12 21 57
2 2 12 16 60
8 8 16 17 55
8 22 26 8 53
10 14 20 12 55
8 10 8 16 65
2 4 16 18 79
10 6 4 11 66
20 32 34 12 36
2 4 6 12 62
4 6 8 20 69
8 12 16 17 46
12 14 16 17 56
2 6 6 15 56
14 4 10 13 53
42 42 38 4 20
10 10 16 16 63
0 0 2 18 75
0 6 10 21 72
2 4 6 22 67
4 4 8 15 76
2 4 2 17 79
0 2 12 17 67
0 0 0 27 81
2 6 6 17 60
8 12 16 15 54
2 0 6 21 98
16 12 18 10 52
6 10 10 13 66
4 4 10 11 58
6 10 6 11 64
10 8 12 21 73
0 0 2 16 69
2 0 2 14 77
0 0 0 22 71
0 2 10 23 79
6 6 10 5 54
0 0 0 16 56
8 8 14 23 55
0 0 0 16 71
0 2 2 20 75
4 6 10 10 60
6 14 8 24 73
0 0 0 19 73
4 6 10 16 63
4 6 10 19 67
2 4 0 16 71
4 2 8 11 58
2 2 2 23 76
12 14 18 7 44
0 2 0 23 81
0 2 4 19 75
0 0 4 19 65
4 6 12 14 71
0 2 0 14 72
2 2 6 20 72
0 0 0 21 79
2 0 0 21 82
4 6 12 14 52
0 6 4 15 61
10 8 12 23 69
0 0 0 23 76
12 6 6 7 53
0 4 2 15 72
0 0 2 19 70
0 0 2 20 84
4 8 8 13 61
4 6 4 18 77
12 20 18 9 44
14 2 10 18 70
4 2 8 9 61
2 2 6 21 71
0 2 6 25 82
10 6 12 14 69
0 0 6 18 70
0 0 2 18 72
2 2 8 11 72
2 4 4 11 72
8 8 12 17 58
2 8 2 24 77
0 4 6 15 75
2 4 6 20 69
10 14 14 10 55
0 0 0 21 75
18 14 16 11 58
24 8 14 8 63
0 0 0 9 69
4 10 6 21 70
0 0 2 19 80
16 14 26 5 61
2 4 2 15 66
0 8 4 12 63
12 20 14 10 58
2 0 2 23 77
8 8 8 20 71
2 2 2 19 70
14 14 14 19 54
4 4 8 22 81
0 2 4 6 79
0 2 2 16 64
2 0 6 11 63
2 6 10 20 73
2 4 6 20 73
4 6 4 13 65
14 12 12 16 58
0 0 0 23 79
10 14 12 14 69
2 6 10 16 74
8 2 12 10 66
2 4 0 11 70
12 0 10 15 71
0 0 0 23 74
4 2 12 16 73
4 2 6 14 66
2 0 2 19 68
0 0 4 24 78
8 4 12 20 67
0 8 6 23 75
0 2 2 18 59
12 20 22 11 53
0 0 4 15 63
2 2 0 12 78
6 10 4 26 79
2 2 2 19 64
10 10 8 19 55
0 0 0 24 83
2 0 0 24 84
8 8 10 18 68
2 2 2 23 66
4 4 10 12 52
2 0 0 16 85
0 0 0 18 73
4 4 2 23 66
4 4 10 20 68
0 0 0 19 77
0 2 0 16 68
2 0 4 15 68
8 6 14 16 60
4 6 8 24 70
2 8 10 17 68
0 0 2 20 73
6 10 12 20 70
12 14 14 15 62
14 12 14 16 58
4 0 4 16 68
4 6 8 14 67
0 0 2 20 64
12 12 14 20 73
2 4 4 21 79
20 18 24 4 51
2 10 8 10 69
0 0 2 19 73
0 2 10 24 70
16 16 20 9 64
0 2 4 11 74
10 12 8 16 70
12 8 14 11 55
16 10 16 8 55
8 6 10 22 68
4 8 4 18 73
10 16 16 17 65
4 0 2 15 63
0 0 0 23 78
2 4 6 17 74
0 2 0 21 72
14 8 20 15 42
6 12 14 18 64
0 0 0 19 56
6 12 8 8 56
2 2 8 24 77
10 6 10 20 69
4 4 6 11 59
6 2 4 20 68
4 4 10 16 67
0 0 0 19 86
10 10 12 17 60
4 4 4 22 70
10 6 4 16 64
6 10 6 10 60
8 8 8 21 73
4 6 10 14 66
10 10 6 18 63
0 2 2 21 88
6 8 8 14 66
18 16 18 5 44
2 12 14 14 70
0 2 0 23 82
0 4 4 14 61
0 0 0 20 84
4 0 8 12 64
14 22 12 14 53
10 8 14 12 51
0 2 0 12 67
0 4 2 19 68
0 0 0 19 74
2 2 6 17 76
8 6 12 16 58
6 4 2 14 67
2 2 8 20 80
6 12 16 8 53
10 18 14 18 56
2 4 8 13 63
10 18 14 10 67
6 10 14 13 52
18 14 20 7 49
10 10 12 16 68
0 4 4 16 86
6 8 10 24 84
6 2 0 21 75
0 0 0 21 64
14 8 14 20 65
0 0 2 20 72
2 0 4 16 63
12 10 12 16 55
0 0 0 24 78
2 0 6 23 68
2 0 2 15 74
0 2 4 21 78
6 0 2 17 72
0 0 2 22 79
6 10 8 16 70
10 10 4 18 60
0 0 2 22 73
16 14 16 15 58
4 2 8 22 69
6 6 14 12 55
0 0 0 19 81
0 0 0 20 76
0 4 4 21 78
4 2 8 22 73
12 14 14 20 67
2 12 10 17 80
2 2 2 23 81
2 0 4 21 71
6 8 12 20 65
4 0 6 9 61
2 6 2 7 63
8 8 18 14 57
0 2 6 24 68
6 8 10 20 63
6 2 6 15 83
0 0 0 23 72
0 0 2 18 91
0 0 0 16 72
0 6 4 16 58
0 0 0 23 86
4 4 10 24 67
0 0 6 17 65
0 0 0 22 79
0 4 8 22 75
14 14 14 16 53
0 4 4 16 65
0 0 2 23 79
0 0 0 20 81
12 10 18 12 63
18 14 14 4 72
0 0 2 19 71
6 6 16 8 59
4 10 8 13 67
10 14 20 16 61
0 0 0 21 68
4 0 8 18 65
6 12 22 18 61
0 0 0 8 60
2 2 8 24 74
4 8 10 24 76
16 12 12 18 62
4 6 6 20 64
4 4 2 19 79
0 2 4 13 63
0 0 0 25 88
22 14 28 12 46
0 0 0 11 66
10 8 14 8 66
4 12 14 18 63
0 2 6 24 75
0 0 2 8 72
6 10 8 15 62
2 8 14 23 77
6 14 16 16 58
2 2 8 14 63
0 4 4 23 88
2 4 8 13 71
10 4 8 19 73
14 12 14 13 52
2 6 10 18 84
2 4 6 17 70
24 14 10 21 72
14 14 14 12 43
6 8 10 9 67
10 10 14 14 58
0 0 0 23 74
8 8 12 6 42
0 0 2 12 68
12 8 12 11 53
0 0 2 23 82
18 6 12 7 51
8 20 26 12 55
12 8 14 7 54
2 2 8 12 63
4 6 8 13 77
2 2 2 20 71
0 0 2 22 79
0 4 8 18 69
2 0 6 19 76
0 0 0 20 86
6 12 14 12 61
12 16 24 14 37
6 2 2 14 70
2 2 8 24 60
0 0 0 17 73
0 0 0 24 81
14 12 12 19 58
4 2 2 18 66
4 6 12 17 65
0 2 2 23 84
0 0 0 16 68
0 0 4 20 70
8 10 10 14 72
2 4 6 25 78
0 0 0 20 73
10 6 8 13 60
0 6 10 22 76
8 14 20 13 59
0 0 0 19 66
12 2 12 15 47
2 6 10 16 64
2 2 2 18 76
0 2 2 24 66
8 16 12 16 63
2 2 4 21 73
6 14 8 16 60
8 14 16 23 74
16 16 14 11 55
2 2 0 22 86
2 4 8 25 77
4 2 6 16 70
12 16 10 8 69
6 6 12 15 58
0 0 2 12 79
12 10 16 20 53
6 4 6 20 68
2 4 8 18 75
0 2 8 17 79
2 6 4 17 73
22 20 26 22 39
4 4 10 15 67
12 6 12 13 60
2 4 6 18 61
2 6 6 20 74
2 6 12 12 69
16 14 18 9 44
2 0 4 12 69
6 8 12 21 64
6 4 12 18 67
2 2 6 16 69
6 8 10 17 65
0 0 2 16 56
;
proc cancorr;
var x1-x3; /*定义x1-x3为一组变量*/
with y1-y2; /*定义y1-y2为另一组变量*/
run;
结果: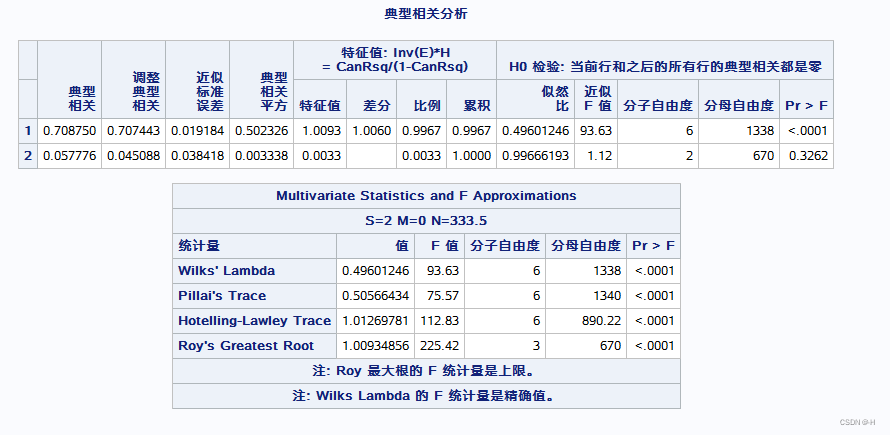
2.结构方程模型(calis lineqs)
示例:
data ex;
input PHD1 PHD2 PHD3 PHD4 PHD5 PHD6 PHD7 PSD1 PSD2 PSD3 PSD4 PSD5 @@;
datalines;
5 5 5 5 5 5 5 4 5 5 5 5
4 4 4 5 5 5 4 4 5 5 5 5
5 5 5 5 5 5 5 5 5 5 5 5
5 4 5 5 5 5 5 4 5 4 4 4
4 4 4 5 5 4 4 4 4 5 4 5
4 5 4 5 5 5 5 5 5 5 4 5
5 4 5 4 5 5 5 5 5 5 2 5
5 5 5 5 5 5 5 5 5 5 5 5
4 4 4 5 5 5 4 5 3 5 5 5
3 3 3 4 3 3 4 3 3 4 3 3
5 5 4 5 5 4 5 4 4 5 4 4
5 4 2 3 5 4 4 4 4 4 2 3
4 5 4 5 5 5 4 4 4 4 5 5
5 5 5 5 5 4 2 4 5 5 4 5
2 3 3 3 4 4 3 3 3 3 4 4
4 5 2 5 4 4 3 4 5 4 4 4
4 4 5 5 5 5 2 5 5 5 4 5
4 5 4 5 5 5 5 4 4 3 4 4
4 5 4 4 4 5 4 5 5 5 5 5
3 5 5 5 5 4 3 4 5 4 4 4
3 3 4 4 3 4 3 2 3 2 2 3
3 3 4 4 3 4 3 2 3 2 2 3
5 5 5 5 5 5 5 4 4 4 5 4
5 5 3 5 5 5 5 5 4 5 4 5
3 3 4 5 5 5 4 3 3 4 3 3
3 3 3 4 3 4 4 3 3 4 3 3
4 4 1 4 5 4 3 3 3 4 3 3
4 4 3 5 5 5 4 4 4 4 2 3
4 4 3 3 3 3 4 4 3 3 4 4
3 3 4 4 4 4 3 2 3 2 2 3
5 5 4 5 5 5 5 4 4 4 5 4
5 5 3 5 5 5 5 3 5 5 5 5
2 4 2 2 5 5 3 4 4 4 3 4
4 5 2 4 5 4 5 5 4 5 5 5
5 5 5 5 5 5 5 5 5 5 5 5
5 2 3 5 5 3 3 5 5 5 5 5
3 3 4 4 3 3 4 4 4 3 3 3
4 4 4 5 5 4 2 4 4 4 4 4
5 5 5 5 5 5 5 5 5 5 5 4
5 5 5 4 5 5 5 5 5 5 5 5
3 3 4 4 5 3 4 3 4 4 3 4
5 5 5 5 5 5 5 5 4 5 5 5
5 4 4 4 5 5 5 1 4 4 4 4
1 3 1 4 5 4 3 2 2 3 2 2
4 3 3 4 4 3 4 4 4 4 4 4
5 5 5 5 5 5 5 5 5 5 5 5
1 5 5 5 5 5 5 5 4 5 5 5
3 3 1 4 5 4 3 3 3 3 3 4
3 3 1 4 5 4 3 3 3 3 3 4
2 3 3 3 3 3 3 2 2 3 4 3
2 3 3 3 3 3 3 2 2 3 4 3
5 4 5 5 5 5 4 4 4 4 2 4
1 3 1 4 5 4 3 2 2 3 2 2
1 2 5 5 5 5 5 4 5 4 4 5
1 5 3 5 5 5 2 5 5 5 5 5
3 5 4 5 5 5 4 3 4 4 3 4
4 4 1 4 4 4 4 4 2 3 2 3
4 4 3 5 5 4 5 4 3 4 4 4
3 4 3 5 5 5 3 4 5 5 4 5
5 5 4 5 5 5 4 4 4 4 3 3
5 5 5 5 5 5 5 3 2 4 4 4
4 3 2 4 2 3 5 4 3 2 2 3
4 4 5 5 3 5 5 5 5 5 5 5
4 3 2 5 5 5 3 3 4 4 3 4
4 3 4 3 3 3 4 4 3 4 3 3
5 5 5 5 5 5 5 5 5 5 4 5
5 4 4 3 5 3 3 4 4 4 4 4
5 5 5 5 5 5 5 4 5 5 4 4
5 5 3 5 5 5 5 2 3 4 3 3
2 1 4 5 5 5 5 5 5 4 4 5
3 4 1 1 3 2 3 2 2 2 1 2
5 5 5 5 5 5 5 5 5 4 5 4
3 5 5 5 3 3 3 5 5 5 5 5
5 5 4 5 5 5 5 4 5 5 5 5
1 3 3 4 4 4 3 4 3 2 2 3
2 2 2 2 3 3 3 2 2 3 2 1
2 2 2 5 5 5 4 4 4 4 3 3
2 2 2 5 5 5 4 4 4 4 3 3
5 5 5 5 5 5 5 4 5 5 5 5
1 2 1 1 4 4 4 3 4 4 3 4
1 2 1 1 4 4 4 3 4 4 3 4
2 5 4 5 5 5 5 5 5 5 5 5
5 5 5 5 5 5 5 4 5 5 2 4
3 3 1 4 4 4 2 3 3 3 2 2
3 3 1 4 4 4 2 3 3 3 2 2
5 5 5 5 5 5 5 4 4 5 4 4
5 5 5 5 5 5 5 5 5 4 4 4
3 3 2 3 3 3 2 2 2 4 3 2
3 3 2 3 3 3 2 2 2 4 3 2
5 5 5 2 2 2 5 4 5 5 5 5
3 4 1 1 4 4 3 3 4 2 2 3
5 5 5 5 5 4 2 5 4 4 4 5
2 5 3 3 2 3 3 4 4 5 4 4
2 5 3 3 2 3 3 4 4 5 4 4
3 2 3 4 4 4 3 3 3 4 3 3
1 1 5 5 5 3 5 4 4 4 4 4
5 5 5 5 5 5 5 4 3 5 4 2
5 4 4 5 5 4 3 3 4 4 4 4
1 2 3 4 4 4 3 2 3 3 3 3
2 3 3 5 5 4 5 3 3 4 3 3
3 3 3 3 3 3 3 3 4 3 4 4
5 2 4 5 5 5 2 4 4 4 4 2
2 2 1 3 3 3 4 1 2 2 4 2
4 2 3 4 5 4 4 3 3 3 3 3
4 3 4 4 5 4 4 4 4 5 5 4
2 3 1 4 5 3 1 4 5 5 5 5
5 5 5 4 5 5 5 5 5 4 5 4
3 4 1 1 4 4 3 3 4 2 2 3
2 3 3 2 2 3 2 2 2 3 3 2
2 3 3 2 2 3 2 2 2 3 3 2
2 5 5 5 5 3 5 5 4 5 5 5
5 5 5 5 5 5 4 5 5 5 4 5
5 5 4 5 5 4 1 4 5 5 5 5
5 5 2 5 5 5 5 4 5 5 5 5
1 2 1 2 2 1 1 2 2 1 1 3
5 3 5 5 5 5 5 5 5 5 5 5
2 2 4 5 5 4 3 4 4 5 4 4
1 2 1 2 3 4 3 2 3 3 3 3
1 2 3 4 4 3 1 2 2 2 2 3
4 5 5 5 5 5 5 5 5 5 1 5
4 4 4 2 4 4 4 4 3 2 2 2
1 4 3 5 5 5 4 3 3 4 2 2
4 2 3 3 4 4 4 2 2 2 2 2
5 5 5 2 1 2 5 5 5 5 5 5
5 5 5 5 5 5 5 3 3 3 2 2
5 5 5 5 5 5 5 2 5 4 2 2
5 3 5 5 5 4 5 5 5 5 5 5
5 5 3 5 5 5 5 5 4 5 5 5
5 5 1 5 5 5 3 5 4 5 1 5
5 5 5 5 5 1 5 5 5 5 5 5
1 2 1 2 3 2 1 2 3 2 3 1
3 2 4 3 2 3 2 2 2 3 1 2
1 2 5 5 5 5 5 4 5 5 4 5
1 5 1 5 5 5 5 5 5 5 5 5
2 2 2 2 2 2 2 3 3 3 3 3
5 5 1 3 5 5 5 5 5 4 3 5
5 5 5 5 5 5 5 2 5 4 4 2
4 5 5 5 5 5 5 5 5 5 5 5
4 4 4 4 5 5 5 5 5 5 5 5
5 5 5 5 5 5 5 4 2 4 4 4
5 5 4 5 4 3 2 4 4 5 2 4
5 2 5 5 5 5 5 5 5 5 2 2
5 5 3 5 5 5 5 5 5 5 5 5
2 4 3 5 5 5 4 4 4 5 5 4
5 5 5 5 5 5 5 5 5 5 5 5
3 5 5 5 5 5 1 4 4 5 4 4
1 1 1 2 2 2 2 2 3 2 2 2
1 1 1 2 2 2 2 2 3 2 2 2
5 4 4 5 5 4 5 4 5 5 4 4
4 3 4 4 5 5 4 4 4 5 4 4
4 4 1 3 5 5 3 2 2 5 4 5
5 3 1 5 5 5 3 5 5 5 5 5
3 4 1 3 1 3 3 2 2 2 2 2
3 4 1 3 1 3 3 2 2 2 2 2
4 3 4 4 4 4 4 4 4 3 5 3
4 4 1 5 5 4 4 3 3 3 3 3
1 5 5 5 5 5 5 5 5 5 5 5
5 5 1 5 5 5 5 2 4 4 4 2
2 2 5 5 5 5 5 5 5 5 5 5
2 2 5 5 5 4 5 1 2 3 5 4
4 5 3 3 3 3 2 4 2 3 4 3
3 3 3 2 5 5 5 4 2 5 4 4
4 5 5 2 5 4 5 4 4 5 5 5
5 1 2 5 5 5 5 5 5 5 5 5
1 5 1 5 5 5 5 5 4 4 5 5
4 4 3 3 4 4 3 2 4 1 1 2
4 5 3 4 4 4 4 1 3 4 1 3
1 3 1 5 5 5 4 4 4 4 3 4
5 5 5 5 5 5 5 5 5 5 5 5
5 5 1 5 5 5 5 5 5 5 5 5
1 5 5 5 5 5 5 5 4 5 4 5
5 5 1 5 5 5 1 3 4 3 2 3
5 5 1 3 5 4 2 2 2 2 2 2
5 5 1 3 5 4 2 2 2 2 2 2
3 5 1 5 3 3 3 2 4 2 2 1
4 5 4 4 5 4 4 4 4 4 4 4
5 5 5 5 5 5 3 5 5 5 5 4
2 4 1 3 4 3 1 1 4 4 1 3
2 4 1 3 4 3 1 1 4 4 1 3
1 2 2 2 1 1 1 5 4 5 4 5
4 4 5 5 5 5 5 4 3 4 4 4
5 2 2 5 5 3 5 5 4 5 2 5
4 5 1 5 5 5 4 2 2 2 2 2
4 5 1 5 5 4 4 2 2 4 5 5
1 5 5 5 5 5 5 3 5 5 3 5
3 5 1 4 5 3 4 2 5 5 5 5
5 5 5 5 5 5 5 2 2 4 2 2
4 5 2 5 5 5 2 5 1 5 5 5
5 5 1 5 5 5 5 4 5 5 3 5
1 5 1 5 5 5 5 2 2 2 2 2
4 4 4 3 3 2 2 5 5 5 3 5
5 5 5 5 5 5 5 2 4 5 4 3
4 3 4 5 5 4 4 4 4 4 5 4
5 5 1 5 5 5 1 5 5 5 5 5
4 5 1 5 4 2 5 4 4 4 5 5
1 1 1 1 1 1 1 1 1 1 2 2
2 2 4 4 2 2 3 2 4 5 4 4
5 4 2 3 3 4 3 3 3 4 5 5
5 5 5 1 4 2 3 5 5 5 5 5
5 5 5 5 5 4 4 2 2 4 4 2
5 5 1 5 5 5 3 5 5 5 2 5
5 5 1 5 5 5 5 3 3 5 5 3
3 5 5 5 5 5 1 3 3 2 2 2
5 5 5 5 5 4 4 2 2 2 2 2
5 5 5 5 5 5 5 5 5 5 5 5
5 2 1 5 5 5 2 4 5 5 5 5
2 5 5 5 5 5 1 5 5 5 5 5
4 4 3 5 5 5 3 3 3 2 2 4
5 5 5 5 5 5 5 5 5 5 5 5
2 2 1 1 1 1 1 1 1 1 2 1
2 2 1 1 1 1 1 1 1 1 2 1
4 4 1 3 5 4 3 3 3 3 2 2
5 2 1 5 5 5 5 5 5 5 5 5
5 4 4 5 5 5 5 4 4 4 3 3
2 5 3 5 5 5 5 5 5 5 4 5
1 1 1 1 1 3 2 1 1 1 1 1
5 5 5 5 5 5 5 3 3 3 3 3
2 2 3 5 5 5 5 4 2 4 4 4
5 2 3 5 5 5 4 2 3 4 3 3
5 5 5 5 5 5 5 5 4 5 4 5
2 2 1 1 1 1 1 1 1 1 2 1
3 3 4 5 5 4 5 4 3 4 5 5
1 2 2 4 4 3 2 4 2 5 4 4
5 5 5 5 5 5 5 1 1 5 1 5
1 5 1 3 5 4 5 4 5 5 2 5
5 5 4 5 5 5 5 2 1 5 5 5
1 5 1 2 5 2 2 2 3 3 4 3
4 5 2 5 2 3 4 5 4 4 4 4
5 5 4 5 5 5 5 5 5 5 4 5
5 4 3 3 4 4 3 5 3 4 4 3
1 5 4 5 5 5 5 1 4 4 2 4
5 5 3 4 5 5 4 5 5 5 3 5
3 5 5 5 5 4 4 4 5 5 5 5
3 3 1 3 5 4 2 3 4 4 4 4
3 3 1 3 5 4 2 3 4 4 4 4
1 2 1 1 1 1 1 1 1 1 1 1
4 4 5 5 5 5 4 2 2 3 3 4
2 3 3 4 5 3 2 4 4 4 2 1
2 2 5 1 2 2 5 2 5 5 5 4
3 4 1 2 3 3 3 4 4 4 4 4
5 4 4 5 5 4 5 1 2 5 5 5
4 4 3 3 3 3 3 4 3 3 3 3
4 5 1 5 5 3 5 5 5 5 3 5
5 5 1 5 5 5 5 4 2 2 1 4
4 1 5 2 5 5 4 2 2 1 2 4
5 5 5 5 5 5 5 4 4 4 2 4
3 5 1 5 5 5 3 3 3 4 4 4
1 5 1 5 5 3 5 3 1 5 4 5
4 4 3 4 3 5 5 4 4 3 4 3
2 5 2 5 5 5 2 4 5 5 5 5
3 3 3 3 3 3 3 5 4 4 1 1
1 2 2 5 5 5 2 2 4 4 2 4
2 2 1 3 2 3 1 5 1 5 4 4
5 5 5 5 5 5 5 2 2 2 2 2
2 2 2 2 2 2 2 2 3 3 2 2
2 2 2 2 2 2 2 2 3 3 2 2
5 5 3 5 5 5 5 1 1 5 3 2
5 5 1 1 5 4 5 1 2 2 4 1
1 1 1 1 2 2 2 3 3 4 5 4
1 1 1 1 2 2 2 3 3 4 5 4
5 4 2 4 2 2 5 4 4 4 5 4
5 5 3 5 3 2 4 5 5 3 5 5
5 5 1 5 1 2 5 4 5 4 3 2
2 2 2 5 5 5 5 5 5 5 5 5
2 5 1 5 5 5 5 4 2 5 4 4
5 5 2 5 2 2 5 2 2 5 2 2
1 5 1 5 5 5 3 4 4 4 4 5
4 5 1 5 5 5 3 4 5 4 4 4
1 1 1 3 5 4 5 4 4 4 4 4
5 2 5 5 5 5 5 1 4 5 2 4
5 2 1 5 1 4 5 1 4 4 1 4
5 1 1 2 2 2 5 5 4 4 2 2
1 5 5 5 4 4 5 2 2 3 1 2
5 5 1 5 5 5 5 4 4 4 5 5
5 5 4 5 3 3 5 2 2 2 2 2
4 5 1 5 5 4 5 2 4 5 5 5
5 5 5 5 5 5 5 5 4 4 5 5
5 1 1 5 5 5 5 1 4 5 4 4
5 5 3 3 5 3 4 1 5 5 5 5
5 5 2 5 5 5 5 5 5 5 5 5
1 5 1 5 5 2 4 2 3 5 3 3
5 4 5 5 5 5 5 5 5 5 4 5
4 5 2 5 5 5 5 2 4 4 1 2
4 2 4 5 5 5 5 3 4 4 2 4
5 2 5 5 5 5 1 2 4 4 4 4
5 5 5 5 5 5 5 2 2 2 5 5
5 5 5 5 5 5 5 1 2 2 4 5
2 2 2 3 4 3 5 5 1 5 4 4
1 2 5 5 5 5 5 4 4 2 1 2
5 5 5 5 5 5 5 5 5 5 5 5
3 5 3 5 5 2 5 5 5 4 4 4
2 3 2 4 3 1 2 4 2 2 1 2
2 2 3 5 5 5 5 5 5 5 4 5
4 5 1 5 5 5 4 2 3 5 4 3
2 2 2 2 5 5 2 5 5 5 5 5
;
run;
proc calis data=ex method=ml toteff mod;
lineqs PHD1 = F1 + e1, /*lineqs语句列出方程组*/
PHD2 = a2 F1 + e2, /*e2表示误差*/
PHD3 = a3 F1 + e3,
PHD4 = a4 F1 + e4,
PHD5 = a5 F1 + e5,
PHD6 = a6 F1 + e6,
PHD7 = a7 F1 + e7,
PSD1 = F2 + e8,
PSD2 = a9 F2 + e9,
PSD3 = a10 F2 + e10,
PSD4 = a11 F2 + e11,
PSD5 = a12 F2 + e12,
F2 = a13 F1 + e13;
std e1-e13 F1=14*var; /*std:定义变量的方差名字*/
run;
总结
以上为全部内容,共涉及12大类SAS基本统计分析语句。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容









所有评论(0)