实验目的与要求：

1. 了解各种数据类型在计算机中的表示方法
2. 掌握C语言数据类型的位级表示及操作

实验环境：

1. 计算机（Intel CPU）
2. Linux操作系统

实验步骤：

1. 安装gcc-multilib：

输入sudo apt-get install gcc-multilib如fig1.

Fig1：安装gcc-multilib（1）

     或者切换超级用户，再输入apt-get install gcc-multilib如fig2.

Fig1：安装gcc-multilib（2）

Fig2：f1安装好界面

安装编译环境：

gcc —v

Fig3：安装编译环境

2.根据bits.c中的要求补全以下的函数：

int bitXor(int x, int y);

int tmin(void);

int isTmax(int x);

int allOddBits(int x);

int negate(int x);

int isAsciiDigit(int x);

int conditional(int x, int y, int z);

int isLessOrEqual(int x, int y);

int logicalNeg(int x);

int howManyBits(int x);

unsigned float_twice(unsigned uf);

unsigned float_i2f(int x);

int float_f2i(unsigned uf);

首先把要做实验的东西放到一个文件夹中

Fig4：打开实验的文件夹

然后点击在终端打开

Fig5：在终端打开

输入 vi bits.c,补全其中的代码

Fig6：打开bits.c

补全后的代码如下图所示：

Fig7：修改前

Fig8：修改后

 

3.在Linux下测试以上函数是否正确，指令如下：

*编译：./dlc bits.c

*测试：make btest

./btest

实验过程及内容：(打开bits.c_中文说明.txt)

1. int bitXor(int x, int y);                //异或操作

1. 题目描述：                  

仅允许使用~和&来实现异或

例子: bitXor(4, 5) = 1

允许的操作符: ~ &

最多操作符数目: 14

1. 思路：

列出两个输入时异或的真值表

x	y	output
0	0	0
0	1	1
1	0	1
1	1	0

Output=(∼x&y)∣(x&∼y)

又因为按位或不为合法运算符，只能使用~与&运算符。固由摩根定律可得：

Output = (∼x&y)∣(x&∼y)=∼(∼(∼x&y)&∼(x&∼y))

1. 代码实现

Fig9：函数一代码

 

1. 思路：

对于32位整数，最小值-231即为0X 8000 0000，即将1左移31位。

Fig10：函数二代码

3.int isTmax(int x);

1. 题目描述：

如果x是最大的二进制补码，返回1；否则，返回0

允许的操作符: ! ~ & ^ | +

最多操作符数目: 10

1. 思路：

法一：或者取反+1

法二：可以知道，最大值为0x7fff ffff，加一后将变为0x8000 0000，且此数加上本身后将变为0。本身加本身为0的数只有0和0x8000 0000，因此，只需将0xffffffff排除即可：

Fig11：函数三代码

1. int allOddBits(int x);

1. 题目描述

如果所有奇数位都为1则返回1;否则返回0

例子： allOddBits(0xFFFFFFFD) = 0，allOddBits(0xAAAAAAAA) = 1

允许的操作符: ! ~ & ^ | + << >>

最多操作符数目: 12

1. 思路：

在二进制下，有且仅有所有位为奇数的数与0x5555 5555进行与运算后由0xffff ffff，变为0x0000 0000。因此可以通过对其与0x5555 5555进行与运算并取反再进行取逻辑反获得结果。又因为题干中不允许使用大于256的整数，故需要通过一些操作获得0x5555 5555。

可以通过将0x55分别进行左移8、16、24得到3个数，并将3个数求和获得0x5555 5555。

Fig12：函数四代码

1. int negate(int x);

1. 题目描述

返回x的相反数（-x）

例子: negate(1) = -1.

允许的操作符: ! ~ & ^ | + << >>

最多操作符数目: 5

 

1. 思路：

即取反并加一返回即可。

Fig13：函数五代码

 

1. int isAsciiDigit(int x);

1. 题目描述

如果x是ascii码中的0~9，返回1;否则返回0

例子: isAsciiDigit(0x35) = 1.

isAsciiDigit(0x3a) = 0.

isAsciiDigit(0x05) = 0.

允许的操作符: ! ~ & ^ | + << >>

最多操作符数目: 15

1. 思路：

即对于每个输入的x，需要满足x>=‘0’且x<=‘9’，因此可以将x与临界值进行作差。并通过右移31位判断对符号位进行判断是0还是1即可。

Fig14：函数六代码

7.int conditional(int x, int y, int z);

1. 题目描述

实现x？y:z

例子: conditional(2,4,5) = 4

允许的操作符: ! ~ & ^ | + << >>

最多操作符数目: 16

1. 思路：

对于x的判断可以通过t=!x进行判断实现，当x为0时返回1；当x不为0时返回0。因此，可以将表达式大致转成( _ &y)|( _ &z)的格式进行配凑。

对于前面的，当x不为0，即t=0时，需要 t转换为0xffff ffff（-1）。可以通过对1按位取反再加一1获得。

对于后面的，当x为0，即t=1时，也需要 t转换为0xffff ffff（-1）。此时直接对t进行取反并加一即可。

Fig15：函数七代码

8.int isLessOrEqual(int x, int y);

1. 题目描述

    如果x<=y返回1否则返回0

例子: isLessOrEqual(4,5) = 1.

允许的操作符: ! ~ & ^ | + << >>

最多操作符数目: 24

1. 思路：

首先应该很容易会想到直接采用y-x并判断符号位的方法进行判断，但如果作差相减，有可能会发生int类型溢出，因此需要考虑其他方法。

1.当x，y同号：此时，即可将问题转化为转换为p=y-x>=0，并对p的符号位（通过右移获得）进行判断，获得运行结果。

2.当x，y异号：此时只要x>=0，就可以返回0，否则返回1。

3.是否同号的判断：可以通过对符号位进行求和判断是否同号。

Fig16：函数八代码

9. int logicalNeg(int x);

1. 题目描述

实现！运算符的功能

例子: logicalNeg(3) = 0, logicalNeg(0) = 1

允许的操作符: ~ & ^ | + << >>

最多操作符数目: 12

1. 思路：

利用其补码的性质，除了0和最小数外其他数，标志位都是互为相反数关系。

0和最小数的补码是本身，不过0的符号位与其补码符号位为0，最小数的为1，不影响。利用这一点得到解决方法。

Fig17：函数九代码

10. int howManyBits(int x);

1. 题目描述

返回将X表示为补码所需的最小有效位数。

例子: howManyBits(12) = 5

howManyBits(298) = 10

howManyBits(-5) = 4

howManyBits(0) = 1

howManyBits(-1) = 1

howManyBits(0x80000000) = 32

允许的操作符: ! ~ & ^ | + << >>

最多操作符数目: 90

1. 思路：

如果是一个正数，则需要找到它最高的一位（假设是n）是1的，再加上符号位，结果为n+1；如果是一个负数，则需要知道其最高的一位是0的。为了方便所以需要将负数取反。

接着从高16位开始检查是否存在1，如果存在则说明至少需要16位，截断x，并检查下一部分。

之后部分以此类推。

Fig18：函数十代码

 

 

11. unsigned float_twice(unsigned uf);

1. 题目描述

以unsinged表示的浮点数二进制的二倍的二进制unsigned型

参数和结果都会被作为unsigned返回，但是会表示为二进制的单精度浮点值。

允许的操作符: 任何整数或者无符号数操作符包括： ||, &&. also if, while

最多操作符数目: 30

1. 思路：

exp表示阶码位、frac表示尾数位）

通过分析可知，共存在三种可能的情况，分别考虑如下：

1.当exp=0xff时，直接返回本身即可；

2.当exp=0时，分两种情况考虑：

当uf[22]=0时，然后将frac左移一位即可

当uf[22]=1时，将exp自增1，然后再将frac左移一位即可

3.对于其他情况，将exp自增1，然后再分两种情况：

当exp==0xff，令frac=0即可。

其余情况正常左移并返回即可

Fig19：函数十一代码

12. unsigned float_i2f(int x);

1. 题目描述

返回int x的unsigned浮点数的二进制形式

参数和结果都会被作为unsigned返回，但是会表示为二进制的单精度浮点值

允许的操作符: 任何整数或者无符号数操作符包括： ||, &&. also if, while

最多操作符数目: 30

1. 思路：

（exp表示阶码位、frac表示尾数位）

首先，我们可以知道int型数据的表示范围为-231~231-1。

通过分析可知，主要有三种情况：

1.用二进制下科学计数法表示int型数时，尾数位数<=23，例如0x00008001，此时将0x8001左移24-16=8位得到frac，而exp则为127+16-1；

2.当尾数位数>23时，找到位数最末一位记作x[i]，然后对尾数的舍去分3种情况考虑，并初始化c=0：

当x[i-1]=1且x[i-2]、x[i-3]…x[0]都为0，且x[i]=1,令c=1；

当x[i-1]=1且x[i-2]、x[i-3]…x[0]不都为0，令c=1;

其余情况 令c=0；

3.特殊情况：

对于x为0或为0x8000 0000的情况，在处理前进行特判即可。

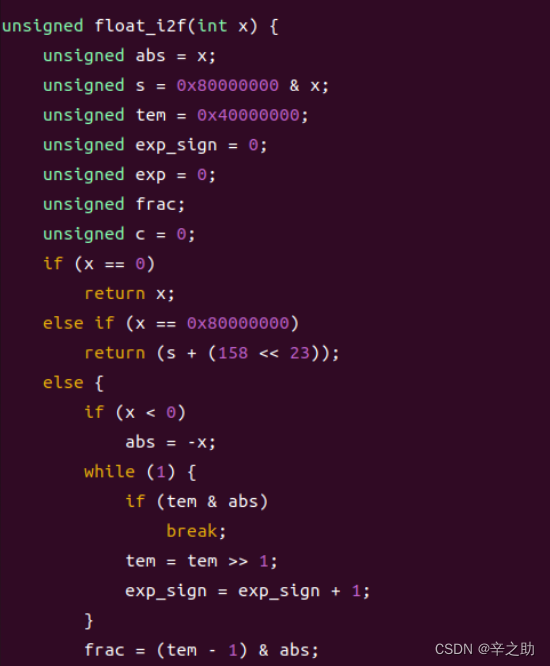
Fig20：函数十二代码

13. int float_f2i(unsigned uf);

1. 题目描述

返回unsigned uf的整型数的二进制形式

参数和结果都会被作为unsigned返回，但是会表示为二进制的单精度浮点值

任何超过范围的数都应该返回 0x80000000u.

允许的操作符: 任何整数或者无符号数操作符包括： ||, &&. also if, while

最多操作符数目: 30

1. 思路：

为了方便进行计算，可以将uf（unsigned float）切割成符号位s，阶码exp和位数frac，分情况讨论：

1.当exp=0或exp-127<0时，返回0；

2.当exp-127>=31时候，超出表示范围，于是返回0x80000000u；

3.当exp-127<=23，根据符号位返回值num>>(23-(exp-127))

（exp表示阶码位、frac表示尾数位）

Fig21：函数十三代码

接着需要对上述修改完的函数是否正确进行测试。

先输入指令：

./dlc bits.c

进行编译

不会吐出任何东西

接着输入make，会有一些警告，但不会影响程序运行。

Fig22：测试

最后输入

./btest

运行程序

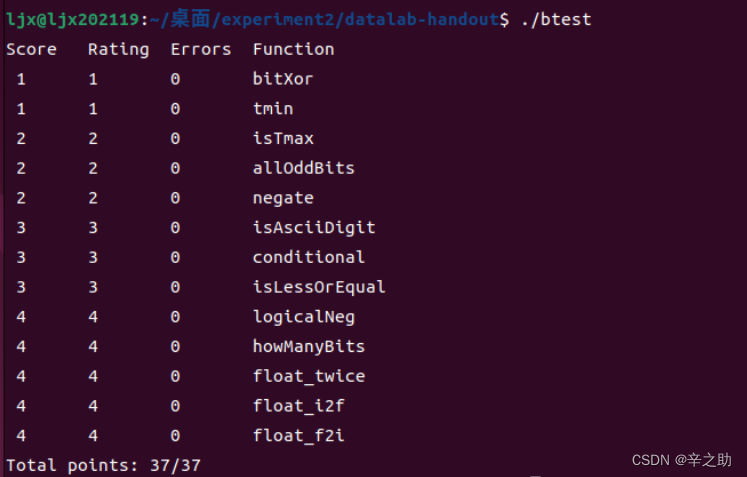
Fig23：测试结果图

可以判断，上述函数全部补充正确！

实验结论：

实验完成了！ 

心得体会：

Vi编辑器还是坏的，所以一开始输入vi bits.c

里面的代码全都是灰色的

这是一开始进去换行又出现了

需要进行以下操作：

1. Vim编辑器的卸载

sudo apt-get remove vim-common （卸载Vim编辑器相关的软件包）

1. 安装Vim

sudo apt-get install vim

完成后即可

还碰到了例如连不了网这种问题，详细叙述以及解决方法放在了实验三！