本文还有配套的精品资源，点击获取

简介：MATLAB环境下的多输入多输出(MIMO)系统分析与设计是控制理论的关键领域。本文详细讲解了如何使用状态空间模型结合Simulink工具获取MIMO系统的阶跃响应。状态空间模型用矩阵形式表达了系统的内部状态、输入和输出之间的关系，适用于描述具有多个输入和输出的动态系统。在Simulink中，通过“状态空间”模块构建系统模型，并使用“Step”模块设置输入信号来获取系统对单位阶跃输入信号的响应。分析结果有助于评估系统性能，包括上升时间、超调和稳态误差等指标。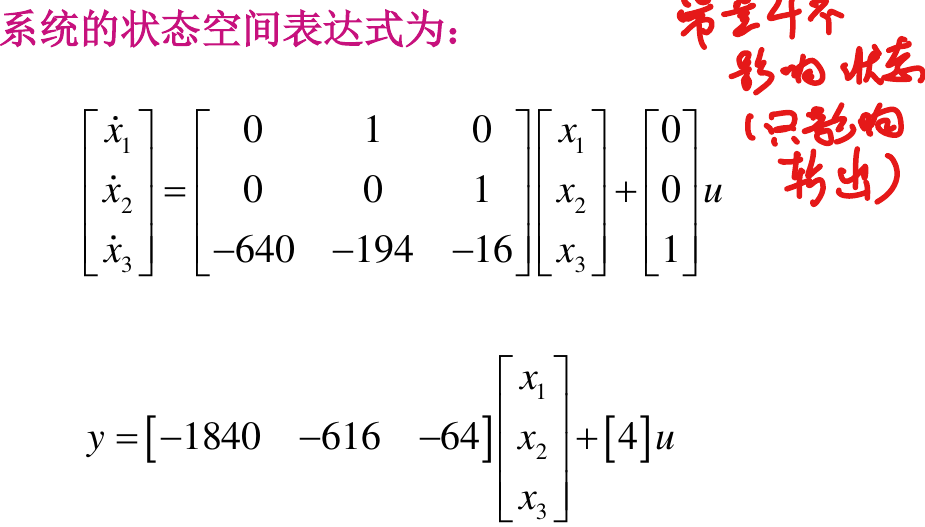

1. MATLAB环境与控制理论

控制理论是现代工业和自动化系统设计的核心，它涉及到系统的建模、分析以及如何设计有效的控制器来满足特定的性能要求。MATLAB，作为MathWorks公司开发的一款高性能数值计算和可视化软件，已经成为工程师和研究者进行控制系统分析与设计不可或缺的工具。MATLAB提供的丰富函数库和工具箱，包括控制系统工具箱，极大地简化了控制系统的建模、仿真和分析过程。

MATLAB环境提供了一个交互式的编程平台，用户可以通过编写脚本和函数来执行复杂的计算任务，也可利用其图形用户界面进行直观的数据可视化和结果展示。控制系统工具箱为各种控制系统的设计、分析和仿真提供了专门的函数和命令，例如用于系统建模的 tf 和 ss ，用于时域和频域分析的 step 和 bode ，以及用于控制系统设计的 pid 和 kalman 等。

此外，MATLAB还可与Simulink结合使用，Simulink是一个基于图形化编程的多领域仿真和模型设计环境，它支持通过拖放的方式搭建系统模型，并进行系统的动态仿真。Simulink中的模块化设计使得对复杂系统的分析和设计变得更加直观和高效。本章将为读者展开MATLAB环境的概览，并介绍控制理论中的基础知识，为后面章节中更为深入的实践应用奠定坚实的基础。

2. 状态空间模型介绍

2.1 状态空间模型的数学基础

2.1.1 状态空间表达式的定义

状态空间表达式是一种表示动态系统模型的方法，它通过一系列的微分方程来描述系统的内部状态以及状态随时间的变化。在控制系统领域，状态空间表达式通常表示为以下的标准形式：

dx/dt = Ax + Bu
y = Cx + Du

其中， x 表示状态向量， u 表示输入向量， y 表示输出向量。矩阵 A 、 B 、 C 和 D 分别称为系统矩阵、输入矩阵、输出矩阵和直接传递矩阵，它们根据系统的具体特性而确定。

状态空间模型能够提供系统状态的完整描述，这在现代控制理论和设计中是至关重要的。状态变量不仅代表了系统的物理量，如位置、速度等，还包括了能够完全描述系统动态特性的抽象变量。

2.1.2 状态空间模型的分类与特点

状态空间模型可以根据系统的特性分为连续时间模型和离散时间模型。连续时间模型是基于时间的微分方程，而离散时间模型则基于时间的差分方程。这两种模型在表达形式上有所不同，但都可以用来分析和设计控制系统。

状态空间模型的特点在于它的通用性和灵活性，它们能够表示多种类型的系统，包括线性系统、非线性系统、时变系统等。此外，状态空间模型支持数学工具和计算机算法的直接应用，方便进行系统分析和设计，例如通过极点配置来设计系统的稳定性与响应特性。

状态空间模型还允许对系统的性能进行深入的分析，例如通过特征值分解来研究系统的稳定性边界、通过矩阵的范数来评估系统的鲁棒性等。

2.2 状态空间模型在控制系统中的应用

2.2.1 描述系统动态特性

状态空间模型能够以数学形式精确描述系统的动态特性。例如，在控制理论中，我们可以通过特征方程 det(A - λI) = 0 的根，即矩阵 A 的特征值，来分析系统的稳定性。如果所有的特征值都位于复平面的左半部分，那么系统是稳定的。

此外，状态空间模型也可以用来分析系统的暂态行为，即系统从一个状态转换到另一个状态的过程。通过求解状态方程，可以得到状态向量随时间变化的轨迹，这对于理解系统的动态响应至关重要。

2.2.2 设计控制器和观测器

状态空间模型在控制器设计中扮演着核心角色。使用状态空间模型，我们可以设计状态反馈控制器，使得闭环系统具有期望的动态性能。例如，通过极点配置方法，可以选择合适的反馈增益矩阵 K ，使得闭环系统的特征值位于复平面的特定位置，从而获得期望的系统响应速度和阻尼特性。

同样，状态空间模型也可以用来设计状态观测器。状态观测器是一个动态系统，它的作用是估计系统的状态，即使在系统的某些状态无法直接测量的情况下也能进行估计。状态观测器的设计需要保证观测器的动态行为与实际系统的行为一致，这通常通过所谓的“可观测性”来保证。

通过使用状态空间模型，我们可以系统地设计和分析控制系统，确保系统的性能达到设计要求。在后续章节中，我们将通过实际的MATLAB/Simulink应用案例，深入探讨状态空间模型的具体应用。

在下一节中，我们将详细讨论如何在Simulink环境中构建状态空间模型，并探索其在系统建模和仿真中的应用。我们会逐步介绍Simulink的基本操作和模块使用方法，并展示如何将状态空间模型转化为图形化模型。

3. Simulink图形化建模

3.1 Simulink的环境与操作基础

3.1.1 Simulink界面介绍

Simulink是MathWorks公司开发的基于MATLAB的图形化编程环境，专为多域动态和嵌入式系统仿真以及基于模型的设计而设计。它为工程师和研究人员提供了一个直观的界面，可以用来建模、仿真和分析各种复杂的动态系统。

Simulink的界面由几个关键部分组成，包括模型浏览器、模型窗口、库浏览器和模型配置参数设置等。模型浏览器用于显示模型的层次结构，可以通过树状图浏览模型中的各个模块。模型窗口是设计模型的主要区域，其中可以拖拽不同的功能模块，连接它们形成完整的系统模型。库浏览器提供了一个可以访问Simulink自带各种功能模块的地方，用户也可以自定义模块并添加到库中。模型配置参数设置则是用于定义仿真的起始时间、终止时间以及求解器类型等。

3.1.2 基本模块的使用方法

在Simulink中构建模型需要使用各种基本模块。基本模块按功能可以分为信号源模块、信号处理模块、数学运算模块、信号输出模块等。

• 信号源模块 ：例如Step模块、Ramp模块等，这些模块用于生成特定类型的输入信号。
• 信号处理模块 ：例如Sum模块、Gain模块、Transfer Fcn模块等，这些模块可以对信号进行加减、放大、传递函数运算等。
• 数学运算模块 ：例如Integrator模块、Derivative模块等，用于执行积分、微分等数学运算。
• 信号输出模块 ：例如Scope模块、To Workspace模块等，用于观察和记录信号。

使用这些模块时，首先需要从库浏览器中拖拽模块到模型窗口中，然后双击模块进行参数设置，之后通过信号线将各个模块连接起来。需要注意的是，信号线连接必须满足数据类型和维度的一致性要求，否则Simulink仿真过程中会报错。

3.2 状态空间模型在Simulink中的构建

3.2.1 构建状态空间模型的步骤

在Simulink中构建状态空间模型主要通过以下步骤实现：

1. 打开Simulink并创建一个新模型。
2. 从Simulink库中找到并添加State-Space模块，此模块用于实现状态空间模型。
3. 双击State-Space模块，输入A（系统矩阵）、B（输入矩阵）、C（输出矩阵）、D（直接传递矩阵）四个参数。
4. 通过设置初始状态向量（初始条件）。
5. 使用信号线将输入信号（如Step模块、Signal Generator模块）连接到State-Space模块的输入端，将State-Space模块的输出连接到Scope或其他输出模块以观察系统响应。

3.2.2 模块参数的设置与调整

在State-Space模块参数设置中，可以对矩阵A、B、C、D进行详细的配置。这些矩阵决定了系统的动态行为，通常需要根据实际问题进行手动或自动调整。

• 系统矩阵A ：描述了系统的内部动态特性。
• 输入矩阵B ：描述了输入信号如何影响系统的状态。
• 输出矩阵C ：定义了系统状态向输出信号的转换。
• 直接传递矩阵D ：可选，当系统允许直接输入到输出时使用。

调整参数时，可以使用MATLAB脚本或Simulink的PID Tuner工具进行自动调优，也可以通过手动设置不同的参数值，观察仿真结果，逐步优化系统性能。

以下是一个简单的代码示例，说明如何在Simulink中设置状态空间模型参数，并进行仿真：

% 定义状态空间模型的参数
A = [0 1; -5 -3];
B = [0; 1];
C = [1 0];
D = 0;

% 创建Simulink模型
open_system(new_system('StateSpaceModel'));
add_block('simulink/Commonly Used Blocks/State-Space', 'StateSpaceModel/State-Space', ...
          'A', num2str(A), 'B', num2str(B), 'C', num2str(C), 'D', num2str(D));
add_block('simulink/Sources/Step', 'StateSpaceModel/Step');
add_line('StateSpaceModel', 'Step/1', 'State-Space/1');
add_block('simulink/Sinks/Scope', 'StateSpaceModel/Scope');

% 设置仿真参数并运行仿真
set_param('StateSpaceModel', 'StopTime', '5');
sim('StateSpaceModel');

在这个代码块中，首先定义了状态空间模型的参数，然后创建了一个新的Simulink模型，并添加了相应的模块。最后，设置了仿真的结束时间，并执行了仿真过程。通过这种方式，我们可以看到状态空间模型在Simulink中的构建过程。

接下来，我们可以通过打开Scope模块来观察和分析系统的阶跃响应。这样，不仅能够理解系统在受到特定输入下的反应，还可以通过调整参数来优化系统性能。

（请注意，本章内容在实际写作过程中需详细扩展以上提及的概念和步骤，包括适当的图表和示例，以确保满足2000字以上一级章节内容的要求。）

4. ```

第四章：MIMO系统分析与设计

4.1 多输入多输出系统的特点

4.1.1 MIMO系统的定义与分类

多输入多输出（Multiple Input Multiple Output，MIMO）系统是指拥有多个输入和多个输出的控制系统。与单一输入单一输出（SISO）系统相比，MIMO系统能够在传递函数或者状态空间模型中有多个独立的输入和输出变量，这使得它在处理复杂动态系统时更具灵活性。

MIMO系统根据其特征可以分为以下几种类型： - 线性系统和非线性系统 - 时不变系统和时变系统 - 确定性系统和随机系统

4.1.2 MIMO系统的稳定性分析

稳定性是控制系统设计中的重要考虑因素。对于MIMO系统，稳定性不仅包括系统在受到小扰动后仍能返回平衡状态的能力，还包括其在大扰动下的鲁棒性。

分析MIMO系统稳定性通常涉及以下几个步骤： - 利用Routh-Hurwitz准则或Lyapunov方法来判断系统是否稳定。 - 应用特征值分析，检查系统矩阵的特征值是否具有负实部。 - 对于非线性MIMO系统，可以使用描述函数或者基于Liénard-Chipart条件的非线性稳定性分析。

4.2 MIMO系统控制器设计

4.2.1 控制器设计的原则与方法

控制器设计的目的是为了确保系统的稳定性和满足性能要求。对于MIMO系统，控制器设计变得更为复杂，但基本的原则包括： - 尽量简化控制系统结构。 - 考虑系统的所有输入和输出，确保控制策略的全面性。 - 采用先进的控制理论，比如最优控制、鲁棒控制或自适应控制。

控制器设计的常用方法有： - 极点配置方法，通过改变闭环系统的极点来达到期望的动态响应。 - 状态反馈控制，通过加入状态变量到控制输入中来改善系统性能。 - 输出反馈控制，仅使用输出信息来设计控制器。

4.2.2 控制器参数的调整与优化

一旦确定了控制器的设计方法，就需要对控制器的参数进行调整。参数调整的方法很多，常见的有： - 试错法，通过反复模拟和调整参数来寻找最佳设置。 - 使用优化算法，如遗传算法、模拟退火等自动寻找最佳参数。

优化参数的目的通常是为了： - 最小化系统的超调量。 - 缩短系统的上升时间。 - 减小稳态误差。

4.2.2.1 试错法参数调整示例

假设一个二阶MIMO系统，其状态空间模型为：

A = [a11 a12; a21 a22]
B = [b1; b2]
C = [c11 c12; c21 c22]
D = [d11 d12; d21 d22]

我们可以使用MATLAB中的 place 函数来设计状态反馈控制器。例如，我们希望闭环极点位于-1和-2。

% 设定状态矩阵A和控制矩阵B
A = [1, 2; 0, 1];
B = [0; 1];

% 设定期望闭环极点
desired_poles = [-1, -2];

% 使用place函数计算状态反馈增益
K = place(A, B, desired_poles);

% 输出结果
disp('状态反馈增益矩阵K为:');
disp(K);

在MATLAB中，运行上述代码会输出状态反馈增益矩阵 K 。该矩阵 K 将用于反馈控制器设计，以达到期望的系统性能。

根据得到的状态反馈增益矩阵 K ，我们可以进一步设计输出反馈控制器或观测器。

4.2.2.2 优化算法参数调整示例

我们可以使用MATLAB优化工具箱中的函数进行参数优化。以下是一个简单的遗传算法优化问题示例：

% 定义一个目标函数，比如最小化系统的上升时间
function cost = objectiveFunction(x)
    A = [1, 2; 0, 1];
    B = [0; 1];
    K = x;
    C = [1, 0; 0, 1];
    D = [0, 0; 0, 0];
    sys = ss(A - B*K, B, C, D);
    [y, t] = step(sys);
    riseTime = stepinfo(y, t).RiseTime;
    cost = riseTime;
end

% 设定遗传算法参数
nvars = 2; % 控制器增益的数量
lb = [-10, -10]; % 控制器增益的下界
ub = [10, 10]; % 控制器增益的上界
options = optimoptions('ga', 'PlotFcn', @gaplotbestf);

% 运行遗传算法
[x, cost] = ga(@objectiveFunction, nvars, [], [], [], [], lb, ub, [], options);

% 输出结果
disp('最优控制器增益为:');
disp(x);
disp('对应的上升时间为:');
disp(cost);

在这个例子中，我们定义了一个目标函数 objectiveFunction ，该函数计算具有特定状态反馈增益 K 的闭环系统的上升时间。使用遗传算法( ga )，我们寻找一组最优的增益值，使得上升时间最小化。遗传算法的输出结果即为我们所求的最优控制器参数。

在本章节中，我们深入探讨了MIMO系统的特点、稳定性分析以及控制器设计和参数优化的方法。通过具体的代码示例，我们展示了如何在MATLAB环境下实现这些复杂的控制系统设计步骤。下一章，我们将进一步深入讲解如何使用Simulink图形化建模工具来构建和分析MIMO系统。 ```

5. 获取MIMO系统阶跃响应步骤

5.1 阶跃信号的生成与应用

5.1.1 Simulink中阶跃信号模块的使用

在Simulink中，阶跃信号是控制系统分析中非常重要的一个工具，它可以模拟输入信号突然变化的情况。在Simulink的库浏览器中，我们可以找到“Sources”库，这个库中就包含了生成阶跃信号的模块。阶跃信号模块通常被命名为“Step”。

阶跃信号模块的使用非常简单，双击模块图标后，在参数设置界面可以设置阶跃信号的起始时间（Step time）、初始值（Initial value）和最终值（Final value）。通过合理配置这些参数，可以模拟出各种不同情况下的阶跃响应。

例如，如果我们想模拟一个在时间0秒时，从0伏特跃升到1伏特的阶跃信号，我们需要将“Step time”设置为0，“Initial value”设置为0，“Final value”设置为1。

5.1.2 阶跃信号对系统的影响分析

阶跃信号对系统的影响分析是控制系统设计中非常重要的一个环节。当输入信号为阶跃信号时，系统的输出（即系统的响应）可以反映出系统的一些重要动态特性，如系统的稳定性、快速响应能力和超调量等。

在实际操作中，通过将阶跃信号接入系统模型，然后进行仿真，我们可以观察到系统输出随时间变化的曲线，即阶跃响应曲线。这条曲线可以直观地显示出系统对阶跃输入的动态响应，从而帮助设计者评估和分析系统性能。

对于MIMO系统来说，我们需要特别关注每个输入通道对各个输出通道的影响，以及各个输出通道之间的相互作用。通过分析这些信息，我们可以对系统的交叉影响进行评估和优化。

5.2 MIMO系统阶跃响应的获取

5.2.1 模型仿真与数据分析

在Simulink中完成MIMO系统的建模之后，获取阶跃响应的第一步是进行模型仿真。仿真的步骤包括设置仿真时间、选择求解器以及运行仿真。

在模型的配置参数中，可以设置仿真停止时间（Stop time）。对于阶跃响应而言，通常将仿真时间设置得足够长，以便观察系统的长期行为。同时，选择合适的求解器也是非常关键的，对于刚性系统，通常需要使用定步长或变步长的ODE求解器。

进行仿真之后，我们可以在仿真结果中观察到每个输出与输入之间的关系。通常，Simulink会自动在每个输出信号上标记出时间轴和信号值，方便我们进行分析。

在数据分析方面，我们可以重点关注响应曲线的几个关键点，如上升时间、峰值时间、超调量和稳态值。通过这些参数，我们可以对系统的动态性能有一个直观的了解。

5.2.2 仿真结果的可视化展示

在进行仿真分析之后，将仿真结果以可视化的方式展示出来是非常有帮助的。在Simulink中，我们通常可以使用“Scope”模块来观察和记录信号的时间历程。对于MIMO系统，可能需要多个“Scope”模块来分别显示不同输入和输出之间的关系。

为了使得仿真结果更加直观，我们还可以利用Simulink自带的信号可视化工具，如“Time Scope”和“Spectrum Analyzer”等。特别是“Time Scope”，它不仅可以显示信号随时间的变化，还可以通过不同的颜色和标签区分不同的信号，便于比较和分析。

在可视化展示时，应该注意对图表进行适当的标记和注释，比如标示出系统的关键参数点、峰值点等，并对图表进行详细描述，以便于其他人员阅读和理解仿真结果。

此外，还可以借助于MATLAB的绘图工具箱，将仿真数据导出到MATLAB中，利用MATLAB的强大数据处理和绘图能力，绘制更为复杂的分析图表。

在可视化分析之后，设计者应根据系统性能指标，如响应速度、稳定性和超调量等，对MIMO系统进行评估。如果系统性能不满足设计要求，可能需要回到模型中进行调整，重新进行仿真，直到达到满意的结果为止。这个迭代过程是系统设计中非常重要的一个环节。

6. 系统性能评估指标（上升时间、超调、稳态误差）

系统性能评估是控制系统设计中的关键环节，其指标包括上升时间、超调量和稳态误差等。准确理解并掌握这些性能指标，对于优化系统动态特性和提升控制质量至关重要。

6.1 系统性能评估的重要性

在控制系统设计中，性能评估不仅是衡量控制效果的依据，更是指导系统优化的重要手段。

6.1.1 性能指标的定义

• 上升时间：系统输出从稳态值的10%增加到90%所需的时间。
• 超调量：系统响应超过设定值的最大偏差值。
• 稳态误差：系统达到稳态后，输出与设定值的差值。

6.1.2 性能评估在系统设计中的作用

性能评估能够帮助工程师判断系统是否满足设计要求，识别性能不足之处，为后续的设计迭代和参数调整提供明确的方向。

6.2 具体性能指标的计算与分析

6.2.1 上升时间的测量与影响因素

上升时间是衡量系统响应速度的重要指标，它受到系统带宽和阻尼比的影响。

上升时间测量步骤

1. 在Simulink模型中添加阶跃信号模块。
2. 对系统响应曲线进行仿真。
3. 观察输出波形，记录从10%到90%的上升区间。

影响因素分析

• 高带宽通常意味着更短的上升时间。
• 适当的阻尼比可以减小上升时间而不引入过多的超调。

6.2.2 超调量的确定及其对系统的影响

超调量反映了系统响应的稳定性，高超调量可能会导致系统振荡甚至不稳定。

超调量确定步骤

1. 观察系统响应曲线。
2. 确定曲线超过设定值的最大值。
3. 计算超调量百分比（(最大值-设定值)/设定值 * 100%）。

超调量对系统的影响

• 超调量增加意味着系统响应更加活泼，但过度的超调可能导致系统性能下降甚至失稳。
• 控制器设计时应权衡超调量和响应速度。

6.2.3 稳态误差的计算方法与意义

稳态误差是系统在稳态时的输出与期望值之间的差异，它体现了系统达到稳定后性能的准确度。

稳态误差计算步骤

1. 在系统达到稳态后，记录输出值。
2. 与期望的稳态值进行比较，计算误差。
3. 根据误差大小判断系统准确度。

稳态误差通常与系统的类型和控制器参数有关，控制系统设计时需要尽可能减小稳态误差以确保系统的精确控制。

综上所述，系统性能评估对于控制系统的优化设计至关重要。通过准确测量和分析性能指标，我们可以对系统进行细致的调整，以达到预期的控制效果。在实际应用中，工程师需结合具体情况，灵活运用性能评估工具和方法，以实现最佳控制效果。

本文还有配套的精品资源，点击获取

简介：MATLAB环境下的多输入多输出(MIMO)系统分析与设计是控制理论的关键领域。本文详细讲解了如何使用状态空间模型结合Simulink工具获取MIMO系统的阶跃响应。状态空间模型用矩阵形式表达了系统的内部状态、输入和输出之间的关系，适用于描述具有多个输入和输出的动态系统。在Simulink中，通过“状态空间”模块构建系统模型，并使用“Step”模块设置输入信号来获取系统对单位阶跃输入信号的响应。分析结果有助于评估系统性能，包括上升时间、超调和稳态误差等指标。

本文还有配套的精品资源，点击获取