本文还有配套的精品资源，点击获取

简介：灰色预测模型GM(1,1)适用于处理数据不完全或含有噪声的复杂系统，通过有限的非线性数据进行趋势预测。本文档提供了一个MATLAB程序包，实现了GM(1,1)模型的构建、参数确定、模型检验和预测等完整步骤。程序包括数据预处理、累加生成序列、模型建立、检验与误差分析、预测及结果可视化，旨在帮助用户理解和应用GM(1,1)模型进行实际预测。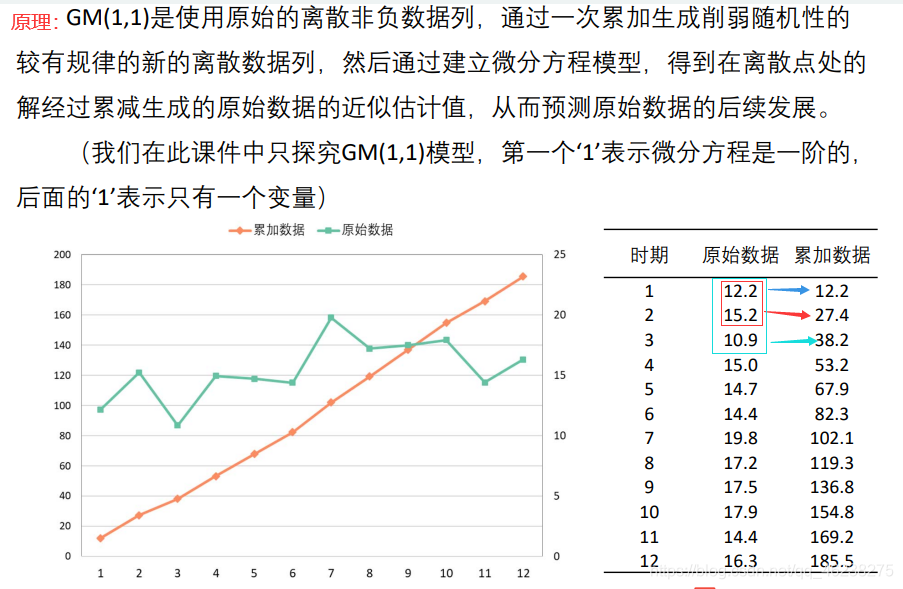

1. 灰色预测模型GM(1,1)介绍

在预测科学领域，灰色预测模型GM(1,1)作为一门新兴的方法论，正逐渐受到学者和工程师们的青睐。GM(1,1)是一种基于灰色系统理论的预测技术，它特别适用于处理信息不完全的系统问题。与传统统计方法相比，灰色预测模型不需要大量历史数据，通过较少的数据就可以有效地预测未来的趋势，这为数据稀缺或不确定性高的领域提供了新的解决路径。

灰色系统的定义与特性

灰色系统理论是由中国学者邓聚龙教授于1982年提出的，它研究的是信息不完全的系统，即系统的内部结构和参数不完全明确的情况。在这样的系统中，部分信息已知，部分信息未知，称为“灰信息”。灰色预测就是建立在这样的理论基础上，通过已知信息构建数学模型进行预测。GM(1,1)模型是灰色预测中的一种基本模型，主要适用于时间序列预测，特别是那些没有明显周期性和随机性的序列。

灰色预测模型GM(1,1)的构建流程

GM(1,1)模型的构建主要分为以下几个步骤： 1. 数据收集：收集与预测目标相关的少量历史数据。 2. 数据处理：对原始数据进行累加生成，以消除随机性。 3. 建立微分方程：根据累加数据建立一阶微分方程。 4. 参数估计：通过最小二乘法估计模型参数。 5. 模型求解：利用微分方程的解析解进行预测。 6. 预测检验：对预测结果进行精度分析和检验。

灰色预测模型GM(1,1)虽然在数据需求上较为宽松，但其预测精度依赖于对建模和参数估计过程的精确控制。在实际应用中，模型的校准和优化是提高预测准确性的关键。接下来，第二章将介绍如何利用MATLAB这一强大的计算工具，来实现GM(1,1)模型，以及如何进行预测和优化。

2. MATLAB在灰色预测中的应用

MATLAB是一种高级的数值计算和可视化软件，它集成了强大的计算能力、丰富的算法库和直观的图形用户界面。在处理数据密集型任务和复杂算法实现方面，MATLAB为研究人员和工程师提供了一个不可多得的平台。本章将深入探讨MATLAB软件的特点和优势，并为实现灰色预测模型（GM(1,1)）的准备工作，包括环境配置和编程基础。

2.1 MATLAB软件概述

2.1.1 MATLAB的发展与特点

MATLAB，即矩阵实验室（Matrix Laboratory），最初由Cleve Moler教授在1980年开发，目的是为了使他的学生能够更容易地使用LINPACK和EISPACK这两个数值分析库。随着其功能的不断扩展，MATLAB逐渐发展成为一种功能全面的工程计算语言。

MATLAB的特点在于其简洁的矩阵操作语法、强大的图形绘制能力和丰富的工具箱（Toolbox）。工具箱是一种特殊的应用程序，它们为特定的学科领域提供了专门的函数集和应用实例。对于灰色预测而言，MATLAB提供了一个数值计算平台，可以用来实现数据处理、算法开发和结果分析等整个流程。

2.1.2 MATLAB在数据分析中的优势

MATLAB在数据分析领域的主要优势体现在以下几个方面：

• 强大的数学计算能力 ：MATLAB提供了广泛的数学函数和操作符，从基本的矩阵运算到复杂的数值算法，用户可以在一个统一的环境中进行开发和测试。
• 丰富的工具箱 ：MATLAB拥有超过100个预定义工具箱，覆盖了从信号处理、图像处理到金融建模的众多领域。这些工具箱为用户提供了丰富的函数和实例代码，极大简化了专业领域的数据分析工作。
• 高效的计算和算法开发环境 ：MATLAB的代码易于编写和调试，而且由于其矩阵操作的高效性，对于需要大量数据计算和矩阵操作的应用而言，MATLAB可以提供比传统编程语言更快的执行速度。
• 直观的图形用户界面 ：MATLAB提供了强大的数据可视化工具，用户可以利用图表、3D图形等方式直观地展示数据和分析结果。

2.2 MATLAB实现灰色预测的准备工作

2.2.1 MATLAB环境配置

在开始使用MATLAB进行灰色预测之前，首先需要完成MATLAB软件的安装和环境配置。以下是配置MATLAB环境的基本步骤：

1. 访问MathWorks官网下载适合您的操作系统版本的MATLAB软件。
2. 安装下载的MATLAB软件。安装过程中，您可以选择安装路径、设置环境变量等选项。
3. 完成安装后，启动MATLAB软件。初次启动可能需要进行产品激活和配置。
4. 安装灰色预测所需的工具箱。如果MATLAB自带的统计和机器学习工具箱未包含所需函数，可以访问MathWorks提供的附加产品目录下载所需工具箱。

2.2.2 MATLAB编程基础

要使用MATLAB进行灰色预测，掌握一些基础的编程知识是必要的。这些基础知识包括：

• 变量和数据类型 ：了解MATLAB中变量的命名规则、基本数据类型（如矩阵、数组、字符串等）。
• 矩阵操作 ：掌握MATLAB中矩阵的创建、访问、操作和函数应用。
• 流程控制 ：学会使用if-else语句、for循环、while循环等控制结构。
• 函数编写 ：理解MATLAB函数的基本结构，学习如何编写自定义函数。
• 图形绘制 ：熟悉MATLAB中plot函数及其他高级绘图函数，掌握如何通过图表展示数据和分析结果。

下面的代码块展示了MATLAB中如何创建一个简单的矩阵并进行矩阵乘法操作，这是一个灰色预测模型实现的基础：

% 创建一个3x3的矩阵
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

% 创建另一个3x3的矩阵
B = [9, 8, 7; 6, 5, 4; 3, 2, 1];

% 计算矩阵乘法
C = A * B;

% 显示结果
disp(C);

对于矩阵乘法操作，矩阵A和B的乘积C被计算出来并显示。这个示例展示了MATLAB中基本矩阵操作的语法和执行逻辑。需要注意的是，进行矩阵乘法前，需要确保矩阵A的列数和矩阵B的行数相等，否则MATLAB会抛出一个错误提示。

通过掌握这些基础内容，您将能够在MATLAB中实现各种复杂的数据分析和模型预测任务，从而为灰色预测模型的实现打下坚实的基础。

3. GM(1,1)模型实现步骤

3.1 数据预处理

3.1.1 数据清洗的重要性

在进行灰色预测之前，数据预处理是一个关键步骤，尤其是数据清洗。原始数据往往包含噪声和异常值，如果不加以处理，将直接影响模型的准确性和可靠性。数据清洗的目的在于提高数据质量，保证数据的一致性和准确性，为后续的模型建立提供干净、可用的数据。

数据清洗的步骤一般包括识别和修正错误数据、处理缺失值、平滑噪声数据、消除异常值以及解决数据不一致性。例如，可以使用统计分析技术来检测和纠正数据集中的错误。此外，缺失值处理方法有删除、填充（使用均值、中位数、众数或者预测模型）等，而异常值则可以通过Z分数、四分位数范围等技术来识别并处理。

3.1.2 数据格式化与归一化处理

数据格式化是指将不同来源的数据整理成统一格式的过程，它包括数据类型转换、数据的标准化和数据的规范化。数据类型转换是为了使数据符合模型输入的要求，例如，将日期时间格式的数据转换成数值型数据。标准化处理通常是指将数据缩放到一个特定的范围，比如0到1之间，或者使数据的均值为0，方差为1。规范化的目的是为了消除不同量纲带来的影响。

归一化处理是数据预处理中一项十分重要的工作，特别是在使用灰色预测GM(1,1)模型时。在GM(1,1)模型中，常采用的方法是对原始数据序列进行累加生成（1-AGO）操作，这实际上是一种归一化手段，可消除原始数据的随机性，增强数据的规律性，使模型更能抓住数据的主要特征。

3.2 原始序列生成

3.2.1 序列生成的数学原理

原始序列生成是建立GM(1,1)模型的起点。灰色预测模型将数据序列作为预测的依据，并通过序列生成的方式来增强数据的规律性。具体来说，通过累加生成新的数据序列，即生成1-AGO序列，这有助于模型捕捉数据的整体趋势，并减弱随机波动的影响。

例如，设原始数据序列为 (X^{(0)}={x^{(0)}(1), x^{(0)}(2), ..., x^{(0)}(n)})，1-AGO序列 (X^{(1)}) 的生成公式为：

[X^{(1)}(k) = \sum_{i=1}^{k} x^{(0)}(i),\ \text{其中}\ k=1,2,...,n]

3.2.2 序列生成的MATLAB实现

在MATLAB中实现1-AGO序列生成的代码示例如下：

% 原始数据序列
original_data = [数据1, 数据2, ..., 数据n];

% 计算1-AGO序列
AGOSeries = cumsum(original_data);

% 打印结果
disp('1-AGO序列:');
disp(AGOSeries);

在上述代码中， cumsum 函数用于计算累加序列，其内部逻辑是将前面所有元素的和作为当前元素。运行代码后，得到的累加生成数据将用于后续的GM(1,1)模型建立。

3.3 模型建立与参数确定

3.3.1 GM(1,1)模型构建过程

GM(1,1)模型的构建过程是一个系统化、有步骤的数学建模过程，具体包括以下步骤：

1. 建立微分方程，将灰变量转化为白变量。
2. 确定微分方程的系数，构建数据矩阵并求解参数。
3. 生成时间响应函数，解出时间序列预测值。
4. 对时间响应函数进行还原，得到原始数据序列的预测值。

GM(1,1)模型的核心是一个一阶微分方程，它反映了累加生成序列的指数变化规律，这个模型可以通过最小二乘法来确定方程中的参数。具体地，GM(1,1)模型可以表示为：

[\frac{dx^{(1)}}{dt} + ax^{(1)} = u]

在这里，(a)和(u)是模型参数，它们通过最小二乘法求得。将1-AGO序列代入该微分方程，通过解微分方程得到还原模型，从而进行预测。

3.3.2 参数估计与MATLAB计算

在MATLAB中实现GM(1,1)模型参数估计的代码示例如下：

% 已知1-AGO序列
AGOSeries = [数据1, 数据2, ..., 数据n];

% 构建数据矩阵B和数据向量Y
n = length(AGOSeries);
B = [-0.5 * (AGOSeries(1:n-1) + AGOSeries(2:n)), ones(n-1, 1)];
Y = AGOSeries(2:n);

% 使用最小二乘法计算参数a和u
parameters = (B' * B) \ (B' * Y);

% a为第一列的参数，u为第二列的参数
a = parameters(1);
u = parameters(2);

% 打印参数
disp(['模型参数a: ', num2str(a)]);
disp(['模型参数u: ', num2str(u)]);

在这段代码中， B 是根据累加序列构建的数据矩阵， Y 是数据向量。然后利用 B' * B 和 B' * Y 进行最小二乘计算得到模型参数 a 和 u 。模型参数是构建GM(1,1)模型的关键，有了这些参数才能计算出模型的预测值。

3.4 模型检验

3.4.1 模型检验的标准与方法

模型检验是灰色预测模型不可或缺的一部分。在GM(1,1)模型中，通常采用后验差检验的方法来判断模型的预测精度。后验差检验包括计算原始数据和残差的方差，以及它们的比值和小概率误差。通过这些统计指标可以判断模型的预测效果。

后验差检验主要包含以下几个统计量：

• 原始数据方差 (S_1^2)：(S_1^2 = \frac{1}{n} \sum_{i=1}^{n} (x^{(0)}(i) - \overline{x})^2)
• 残差方差 (S_2^2)：(S_2^2 = \frac{1}{n} \sum_{i=1}^{n} (\varepsilon(i) - \overline{\varepsilon})^2)
• 方差比值 (C = \frac{S_2}{S_1})
• 小概率误差 (p = P{|\varepsilon(i) - \overline{\varepsilon}| < 0.6745S_1})

其中，(\varepsilon(i)) 是残差，(\overline{\varepsilon}) 是残差平均值。这些统计量分别描述了原始数据的离散程度、残差的离散程度以及预测精度。

3.4.2 模型检验的MATLAB实现

在MATLAB中进行模型检验的代码示例如下：

% 计算还原数据
reduced_data = zeros(size(original_data));
for i=1:n
    reduced_data(i) = (1-a) * (original_data(i) - original_data(1) * exp(-a * (i-1))) / a;
end

% 计算残差
residuals = original_data - reduced_data;

% 计算相关统计量
S1 = std(original_data, 0, 1);
S2 = std(residuals, 0, 1);
C = S2 / S1;
p = sum(abs(residuals - mean(residuals)) < 0.6745 * S1) / n;

% 打印检验结果
disp('方差比值C:');
disp(C);
disp('小概率误差p:');
disp(p);

在这段代码中，首先计算还原数据序列，即通过模型预测的原始数据序列值。然后计算残差序列及其统计量。计算的方差比值和小概率误差用于评价模型的预测精度。一般而言，如果方差比值 (C < 0.35) 并且小概率误差 (p > 0.95)，则模型的精度被认为是好的。

3.5 预测与误差分析

3.5.1 预测步骤与技巧

在建立了GM(1,1)模型并完成模型检验之后，即可开始进行预测。预测过程一般遵循以下步骤：

1. 使用已有的数据序列来建立模型。
2. 利用模型参数进行预测，得到未来时段的预测数据。
3. 对预测结果进行后验差检验，验证模型的可靠性。
4. 根据检验结果调整模型参数或者改进模型结构。

为了提高预测的准确性，可以采取一些技巧，比如分段建模，利用已有的最新数据不断更新模型参数，或者在模型中引入新的影响因素等。这些方法可以增强模型的自适应能力，并使得模型能够更好地反映实际情况的变化。

3.5.2 误差分析与处理

误差分析是灰色预测模型的一个重要组成部分，它可以帮助我们了解预测值与实际值之间的差异，并对模型进行优化。误差分析一般包括以下方面：

• 计算绝对误差和相对误差，分析预测值与实际值之间的偏差程度。
• 绘制误差分布图，直观展示误差的大小和分布情况。
• 分析误差变化趋势，确定是否存在系统误差。

在实际操作中，可以使用以下公式来计算绝对误差和相对误差：

• 绝对误差 (E(i) = |x^{(0)}(i) - \hat{x}^{(0)}(i)|)
• 相对误差 (e(i) = \frac{E(i)}{x^{(0)}(i)})

其中，(x^{(0)}(i)) 是实际观测值，(\hat{x}^{(0)}(i)) 是预测值。

误差分析通常涉及到统计学知识，比如均方误差（MSE）、均方根误差（RMSE）等。这些统计指标有助于量化预测的准确度，并指导模型的调整。

3.6 结果可视化

3.6.1 可视化的目的与意义

预测模型的结果可视化是一个将复杂的数据转换成图形的过程，这有助于我们直观地理解数据和预测结果。在灰色预测模型中，结果的可视化可以呈现预测值与实际值的对比，以及误差的变化趋势，进而辅助决策者作出更明智的决策。

可视化可以通过不同的图表类型来实现，比如折线图、柱状图、饼图等。这些图表能够帮助用户快速识别数据中的模式、趋势、异常值以及潜在的问题。

3.6.2 利用MATLAB进行结果展示

在MATLAB中实现结果可视化的代码示例如下：

% 预测值
prediction = [预测1, 预测2, ..., 预测n];

% 绘制实际值与预测值的对比图
figure; % 创建新图形窗口
hold on; % 保持图形，以便在同一图形上绘制多条曲线
plot(original_data, 'bo-', 'DisplayName', '实际值');
plot(prediction, 'r*-', 'DisplayName', '预测值');
xlabel('时间');
ylabel('数据值');
title('实际值与预测值对比图');
legend;
hold off; % 释放图形

在这段代码中，使用 plot 函数绘制出原始数据和预测值的对比折线图。蓝色的线和圆点代表实际观测值，而红色的线和星号代表预测值。通过这样的可视化方式，可以直观地看出预测值与实际值的吻合程度。

以上就是GM(1,1)模型实现步骤的详细解读。通过本章的学习，您应该对灰色预测模型的构建过程、参数估计、模型检验、预测及结果可视化有了深入的理解，并且能够在MATLAB环境下进行相应的操作。

4. GM(1,1)模型的实际应用领域

灰色预测模型GM(1,1)是应用灰色系统理论来预测和决策的模型之一，它在处理不确定性、不完全信息和小样本数据问题中显示出特有的优势。本章节将探讨GM(1,1)模型在不同实际应用领域中的表现和案例。

4.1 在经济预测中的应用

4.1.1 经济数据的特征与应用

经济数据往往包含大量不确定性和随机性因素，对未来的预测充满挑战。GM(1,1)模型作为一种时间序列预测工具，能够在不完全信息的情况下进行有效的预测。它通过少量的历史数据来构建未来趋势的预测模型，这与经济数据的特点十分吻合。

4.1.2 实际经济案例分析

以某个国家的GDP增长率为例子，过去几年的数据可能呈现出波动趋势，但未来几年的数据是未知的。使用GM(1,1)模型，可以从已知的历史GDP增长率序列中提取出增长规律，进而对未来的GDP增长率进行预测。

% 假设历史GDP增长率为以下数据（单位：%）
historical_data = [1.5, 2.0, 2.5, 2.8, 3.0, 3.1];
% 将数据进行一次累加，得到1-AGO序列
data_1ago = cumsum(historical_data);
% 构建数据矩阵B和数据向量Y
B = [-0.5*(data_1ago(1:end-1)+data_1ago(2:end)), ones(size(data_1ago)-1, 1)];
Y = historical_data(2:end);
% 利用最小二乘法估计参数a和b
a_b = B\Y;
a = a_b(1);
b = a_b(2);
% 建立GM(1,1)模型并进行预测
predict_model = @(x) (historical_data(1) - b/a)*exp(-a*(x-1)) + b/a;
future_years = 3;
forecasted_data = arrayfun(predict_model, (length(historical_data)+1):(length(historical_data)+future_years));
% 输出预测结果
disp(forecasted_data);

在上述MATLAB代码中，通过构建数据矩阵B和数据向量Y，并采用最小二乘法计算模型参数a和b，从而建立GM(1,1)模型，并对未来的三年GDP增长率进行预测。参数分析和模型的逻辑解释将在后面的段落中详细说明。

参数分析和模型逻辑

在GM(1,1)模型中，参数a和b分别表示发展系数和内生控制变量，它们决定了模型的预测行为。发展系数a负值较大时，意味着历史数据变化迅速，未来的预测值将随着预测时间的增加而快速趋向于系统特征值b/a。相反，当a接近于0时，预测曲线趋于水平，表示未来发展变化不大。

MATLAB中的 arrayfun 函数用于应用 predict_model 函数到未来年份的序列上， cumsum 用于计算累积和生成累加序列。通过这种方式，可以清晰地看到模型是如何根据历史数据，利用线性代数和函数运算，对经济数据进行有效预测的。

4.2 在环境科学中的应用

4.2.1 环境监测数据的特性

环境监测数据通常表现出随机性和非线性的特征，灰色预测GM(1,1)模型因其对非线性数据的处理能力，在环境科学中得到了广泛应用。比如，环境中的污染物浓度、河流流量、空气质量指数等数据，都是GM(1,1)模型处理的对象。

4.2.2 环境问题的预测实例

假设我们有一组关于某地区空气质量指数（AQI）的历史数据，运用GM(1,1)模型，我们可以预测未来某个时间点的AQI值，从而为环境保护和治理提供科学依据。

% 假设历史AQI数据如下（单位：无量纲）
aqi_data = [105, 100, 95, 90, 85, 80];
% 类似于之前的步骤，进行1-AGO操作和参数求解
aqi_1ago = cumsum(aqi_data);
B_aqi = [-0.5*(aqi_1ago(1:end-1)+aqi_1ago(2:end)), ones(size(aqi_1ago)-1, 1)];
Y_aqi = aqi_data(2:end);
a_b_aqi = B_aqi\Y_aqi;
a_aqi = a_b_aqi(1);
b_aqi = a_b_aqi(2);
% 利用模型进行AQI预测
predict_aqi = @(x) (aqi_data(1) - b_aqi/a_aqi)*exp(-a_aqi*(x-1)) + b_aqi/a_aqi;
forecast_aqi = arrayfun(predict_aqi, (length(aqi_data)+1):(length(aqi_data)+future_years));
% 输出预测结果
disp(forecast_aqi);

通过此MATLAB代码段，我们不仅可以预测未来某时段的AQI值，还可以根据预测结果进行相应的环境保护措施。预测模型的参数a和b对环境科学问题的预测同样至关重要，它们直接关系到预测的精确性和实用性。

4.2.3 环境预测模型的实际应用与政策建议

在环境预测的实际应用中，模型的预测结果可以指导制定相关的环境政策和措施。比如，根据空气质量预测结果，可以提前采取限制工厂排放、减少机动车行驶等措施，从而有效降低未来的AQI值，改善空气质量。

4.3 在工程技术中的应用

4.3.1 工程数据的收集与处理

在工程领域，数据通常包括项目成本、工程进度、设备故障率等，这些数据往往包含大量的不确定性。GM(1,1)模型能够在不确定性的背景下，通过少量的数据构建出能够反映系统行为的预测模型。

4.3.2 工程项目风险预测案例

以某大型设备的故障率预测为例，设备使用初期故障率较高，随着使用时间的增长和维护措施的完善，故障率逐渐降低。GM(1,1)模型可以利用设备投入使用初期的故障率数据，预测中长期的故障率，为设备的维修和保养计划提供参考。

4.3.3 预测模型的优化与应用展望

GM(1,1)模型在工程领域的应用仍有许多优化空间。例如，可以结合其他预测模型进行集成预测，通过误差反馈机制对模型进行自我修正和调整，进而提高预测的准确度。在工程项目管理中，利用优化后的预测模型，可以更加精确地控制成本、安排进度和降低风险。

在所有这些应用中，GM(1,1)模型为处理不确定性和小样本数据问题提供了一种有力的工具，展示了其在不同领域的广泛应用价值和前景。下一章节将对GM(1,1)模型的优势与局限进行总结，并展望其未来的研究方向和潜在的技术发展。

5. 总结与展望

5.1 灰色预测GM(1,1)模型的优势与局限

优势分析

灰色预测模型GM(1,1)之所以在多个领域得到广泛应用，其主要优势体现在以下几个方面：

1. 数据需求量少 ：GM(1,1)模型对于数据的需求量相对较小，非常适合处理“少数据”问题，这是它的独特优势。
2. 计算简单 ：模型的构建过程简单，不需要复杂的统计推断，易于编程实现。
3. 预测准确 ：在数据量较少但具有趋势性的序列上，GM(1,1)可以取得较好的预测效果。

局限性探讨

然而，GM(1,1)模型并非万能，它也有一些局限性：

1. 适用范围限制 ：该模型更适合于指数型趋势的序列，对于波动较大的数据序列效果不理想。
2. 模型稳定性的考量 ：模型的预测结果稳定性受原始数据质量的影响较大，若原始数据存在较大噪声，会影响预测准确性。
3. 动态适应性不足 ：灰色预测模型在处理具有突变特点的数据时，难以有效反映数据的动态变化。

5.2 未来研究方向与技术发展展望

技术融合与创新

在未来的研发中，可以考虑将GM(1,1)模型与其他预测方法相结合，如神经网络、支持向量机等，利用各自优势构建更为强大的预测模型。此外，人工智能和机器学习技术的快速发展，为灰色预测模型提供了新的优化方向和扩展途径。

模型的改进与优化

对GM(1,1)模型进行改进，以适应更复杂、动态变化的现实情况，将是一个重要的研究方向。例如，通过引入新的参数估计方法，提高模型对数据波动的适应性，以及增加模型的自我调整能力。

实际应用领域的扩展

随着科技的进步，灰色预测模型在更多领域的应用将会被探索和拓展，特别是在数据获取相对困难或者数据量不足的情况下，GM(1,1)模型可以作为一种有力的预测工具。未来的研究可以针对特定领域的需求，进行模型的定制化和专业化改进。

例如，利用GM(1,1)模型进行未来交通流量的预测，可以为智能交通系统提供决策支持；在资源管理和调度中，可以预测能源消耗趋势，优化资源分配策略；在医疗卫生领域，可以预测疾病发展趋势，辅助公共卫生政策的制定等。

在下一章节中，我们将对GM(1,1)模型的实现、应用及其在未来的发展方向进行更深入的探讨，以期望帮助读者更好地理解和运用该模型。

本文还有配套的精品资源，点击获取

简介：灰色预测模型GM(1,1)适用于处理数据不完全或含有噪声的复杂系统，通过有限的非线性数据进行趋势预测。本文档提供了一个MATLAB程序包，实现了GM(1,1)模型的构建、参数确定、模型检验和预测等完整步骤。程序包括数据预处理、累加生成序列、模型建立、检验与误差分析、预测及结果可视化，旨在帮助用户理解和应用GM(1,1)模型进行实际预测。

本文还有配套的精品资源，点击获取