Time-LLM架构分析

Time-LLM：通过重编译大语言模型进行时序预测》，这是一篇24年发表在ICLR上的论文。针对NLP、CV领域的任务，往往一个大模型就能解决各种问题，而时序预测领域的模型却要针对不同任务和应用进行不同的设计。研究表明LLM在复杂的token序列上有强大的模式识别和推理能力，但该，以利用这些能力呢？在这篇工作中推出了一个重编译框架Time-LLM，在保持主体的语言模型不变的情况下，将LLM应用到时

代码不自由

2078人浏览 · 2025-03-02 23:57:46

代码不自由 · 2025-03-02 23:57:46 发布

（俺一个横向项目相关的科研，想用Time-LLM做点时序预测的工作）链接：论文、代码

《Time-LLM：通过重编译大语言模型进行时序预测》，这是一篇24年发表在ICLR上的论文。

针对NLP、CV领域的任务，往往一个大模型就能解决各种问题，而时序预测领域的模型却要针对不同任务和应用进行不同的设计。研究表明LLM在复杂的token序列上有强大的模式识别和推理能力，但该如何将时序数据有效对齐到自然语言的模态，以利用这些能力呢？

在这篇工作中推出了一个重编译框架Time-LLM，在保持主体的语言模型不变的情况下，将LLM应用到时序预测上。经过综合测评后显示，Time-LLM是一个强大的时序学习器，性能优于当时SOTA的专用预测模型，在小样本和零样本学习场景下同样表现优异。

给你个历史的观察序列 $X \in \mathbb{R}^{N \times T}$ ，长 $T$ 个时间步，每一步是一个 $N$ 维变量，希望重编译一个LLM $f(\cdot)$ ，能理解输入的时序序列并准确未来 $H$ 个时间步 $\hat{Y} \in \mathbb{R}^{N \times H}$ ，努力最小化真实值 $Y$ 和预测值之间的均方误差 $\frac{1}{H} \sum_{h=1}^H ||\hat{Y}_h-Y_h||_F^2$ 。

总体上包含3个主要组件：1.变化输入的部分；2.一个预训练好的LLM；3.映射输出的部分。只有1和3这两个轻量级的部分会被更新，主干2是被冻结的，要求可以接收嵌入表示的输入，产生嵌入表示的输出，比如Llama和GPT-2。对视觉语言或其他多模态语言模型进行微调，一般需要成对的跨模态数据，而Time-LLM相反，它可以直接优化，只需要少量的时间序列和训练批次，高效，且与从头构建特定领域的LLM或对它们进行微调相比资源限制更少。还可以无缝集成各类现成技术，以减少内存占用（例如量化）。

首先，将 $N$ 元的时间序列划分成 $N$ 个一元的时间序列，随后每个子序列 $X^{(i)} \in \mathbb{R}^{1 \times T}$ 独立进行处理，步骤如下：1.对 $X^{(i)}$ 进行归一化、切片、嵌入；2.将其转化成LLM可读的格式；3.用LLM进行时序推理；4.LLM生成表示并映射到最终预测值 $\hat{Y}^{(i)}$ 。

如下图中序号所示，其预测的关键步骤有：输入一条历史时间序列后，先通过①进行分片，再由定制的②进行嵌入，然后这些分片的嵌入向量在③会被重编译，以和压缩后的文本进行模态对齐。同时为了增强模型的推理能力，④还会通过添加额外的提示词前缀来指导如何对输入分片进行转换。在⑤这一步，LLM的输出分片被投影到最终的预测结果。

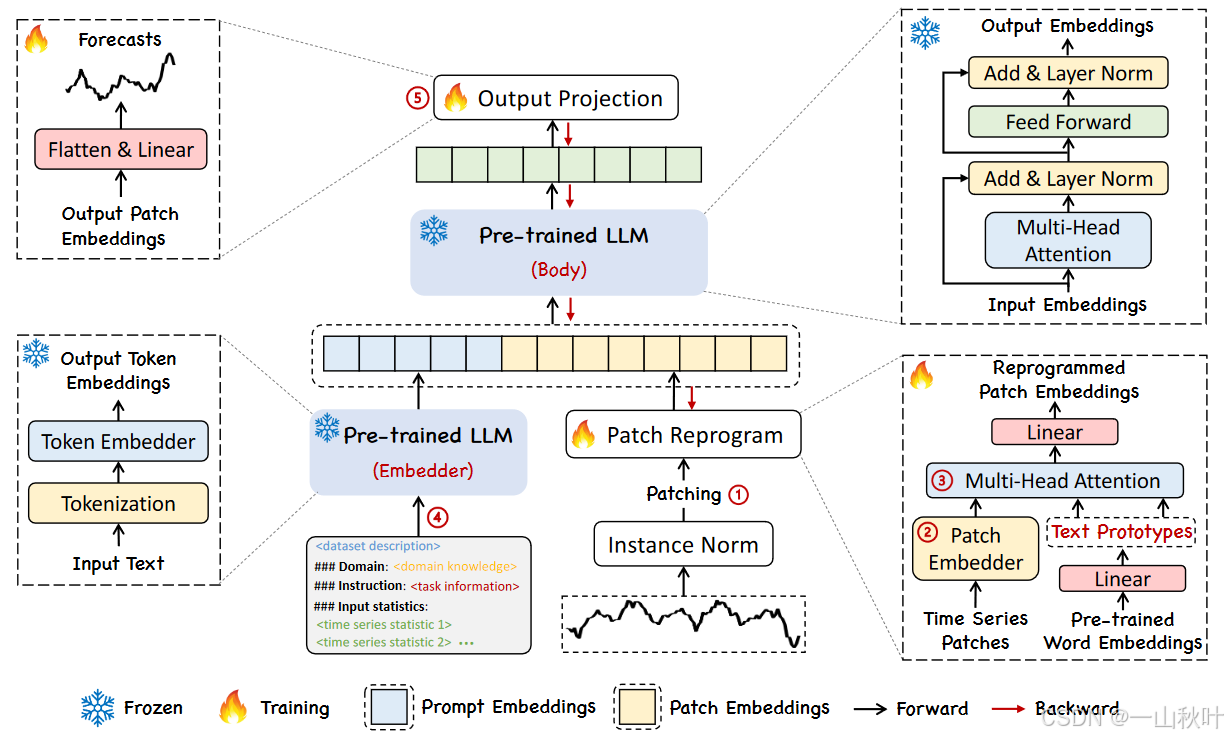
输入嵌入层

对输入样例 $X^{(i)}$ 进行可逆实例归一化（reversible instance normalization，RevIN）,即单独对每个序列实例，而不是整个批次进行正则化，这样能更好地适应动态变化的时间数据，缓解分布漂移。再将 $X^{(i)}$ 划分为几个长度为 $L_p$ 的连续分片，输入的分片数为 $P=\left \lfloor \frac{(T-L_p)}{S} \right \rfloor + 2$ ，其中 $S$ 为水平滑动步长（分片可能存在重叠），这样做的动机有两：1.更好地保留局部语义信息；2.减少序列长度，降低计算复杂度。将这些分片 $X_P^{(i)} \in \mathbb{R}^{P \times L_p}$ ，通过一个简单的线性变化层（全连接层）进行嵌入，映射成 $\hat{X}_P^{(i)} \in \mathbb{R}^{P \times d_m}$ 。

分片重编译

为了将时间序列与自然语言进行模态对齐，作者将分片的嵌入向量重编译到了原数据的表示空间中，以激活LLM在时序数据上的推理能力。一种消除相近模态之间的差异的常用办法是学会往输入数据里添加某种“噪声”，使其适配已预训练好的模型，有时确实可行，已有工作用视觉模型处理跨域图像、重编译声学模型处理时间序列，其中对输入样例的转化都是显式的、可学习的。而时间序列没法显式修改，或者用自然语言进行无损的描述。

作者提出在主干中使用预训练好的嵌入矩阵 $E \in \mathbb{R}^{V \times D}$ 对 $\hat{X}_P^{(i)}$ 进行重编译。此外，还需要告知哪些词在目标任务中有意义的先验知识，不然搜索空间巨大，计算和存储成本高昂，还容易过拟合。于是又对 $E$ 做一个简单的线性变换，筛选出其中最有代表性的嵌入，得到 $E' \in \mathbb{R}^{V' \times D}$ ，其中 $V' \ll V$ 。

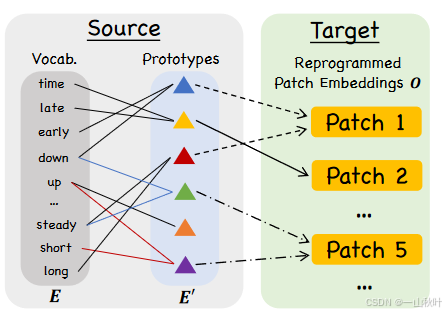
文本学着根据语言线索进行连接，比如上图中红线连接的“short up”和蓝线连接的“steady down”，两相结合便能表示局部分片的信息了（“short up then down steadily”）。这个方法很有效，且能自适应地选择相关联的源信息。具体地，用了一个多头的交叉注意力层，对于每个头 $k=\{1,...,K\}$ ，定义查询矩阵 $Q_k^{(i)}=\hat{X}_P^{(i)}W_k^Q$ 、键矩阵 $K_k^{(i)}=E' W_k^K$ 、值矩阵 $V_k^{(i)}=E' W_k^V$ ，其中各系数矩阵有 $W_k^Q \in \mathbb{R}^{d_m \times d}$ ， $W_k^K, W_k^V \in \mathbb{R}^{D \times d}$ ， $D$ 是主干模型的隐藏层维度， $d=\left \lfloor \frac{d_m}{K} \right \rfloor$ ，对每个注意力头中的时间序列分块进行重编译的操作定义如下：

$z_k^{(i)}=ATTENTION(Q_k^{(i)}, K_k^{(i)}, V_k^{(i)})=SOFTMAX(\frac{Q_k^{(i)}K_k^{(i)T}}{\sqrt{d_k}})V_k^{(i)}$

聚合每个头产生的 $Z_k^{(i)} \in \mathbb{R}^{P \times d}$ ，得到 $Z^{(i)} \in \mathbb{R}^{P \times d_m}$ ，再经过线性映射对齐到主干模型的隐藏维度，生成 $O^{(i)}\in \mathbb{R}^{P \times D}$ 。

提示词前缀

在语言模型中，Prompt 通常指的是在输入文本中加入一些引导性信息（如任务描述、指令等），用来告诉模型我们希望它执行什么样的任务。下图就是一个提示词样例，其中 $\color{blue}{<>}$ 表示具体任务配置，橘色的（这个颜色打不出来）是计算得到的输入统计量。

如果直接将时间序列翻译成自然语言，是很难创建这样的“instruction-following”数据集的，无法有效利用即时提示（on-the-fly prompting，指的是无需预先微调，而是在运行时通过prompt来指导模型完成任务），性能一般。

在一些研究中，将图像这样的数据模态进行集成，作为提示词的前缀，从而促进对输入的有效推理。作者就想着，提示词本身能否作为前缀去丰富输入的上下文，并指导对重编译后的时间序列分片的转换呢？这个理念被命名为Prompt-as-Prefix（PaP），本质上是一种比传统prompt更强的提示方法，它的前缀embedding是可训练的，以更好地让LLM适应特定任务。

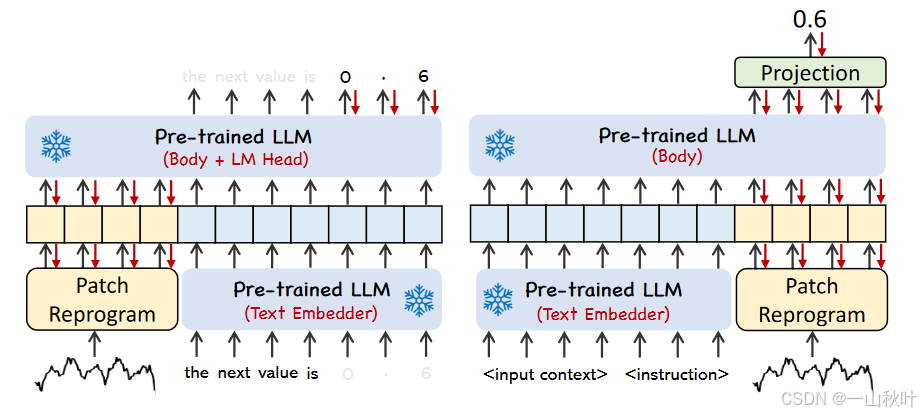
比对一下上图中的两种提示方法。在左图的patch-as-prefix方法中，通过自然语言表达的方式提示语言模型预测时间序列的后续值，这种方法有几个问题：1.LLM主要基于文本训练，会将数字视为token，就不擅长处理高精度数值计算。2.不同的语言模型预训练在不同的语料上，可能采用不同的分词方法来产生高精度数字，比如对同一个数值0.61，LLM可能将其表示成不同的token序列，如[‘0’, ‘.’, ‘6’, ‘1’] 和 [‘0’, ‘.’, ‘61’]，便需要复杂的定制化后处理。

在右图的prompt-as-prefix方法中就巧妙地避开了上述问题，作者认为构建有效提示词的3个关键要素是1.数据集上下文；2.任务指令；3.输入统计量。在图3的prompt示例中，数据集上下文为LLM提供关于输入时间序列的重要背景信息，这些信息在不同的领域中通常表现出不同的特征；任务指令指导LLM针对特定任务对分片的嵌入向量进行转换；额外还要一些重要的统计量（如趋势和滞后）来丰富输入的时间序列，以促进模式识别和推理。

输出映射

最后打包提示词和分片嵌入向量 $O^{(i)}$ ，经过冻结的LLM的前向传递后，丢弃前缀部分便是输出表示了，然后对其进行平坦化和线性映射，得到最终的预测结果 $\hat{Y}^{(i)}$ 。

最后附一张我们垃圾模型的架构图，只能说改动小到查重都过不了的那种(；′⌒`)

2048 AI社区

有“AI”的1024 = 2048，欢迎大家加入2048 AI社区

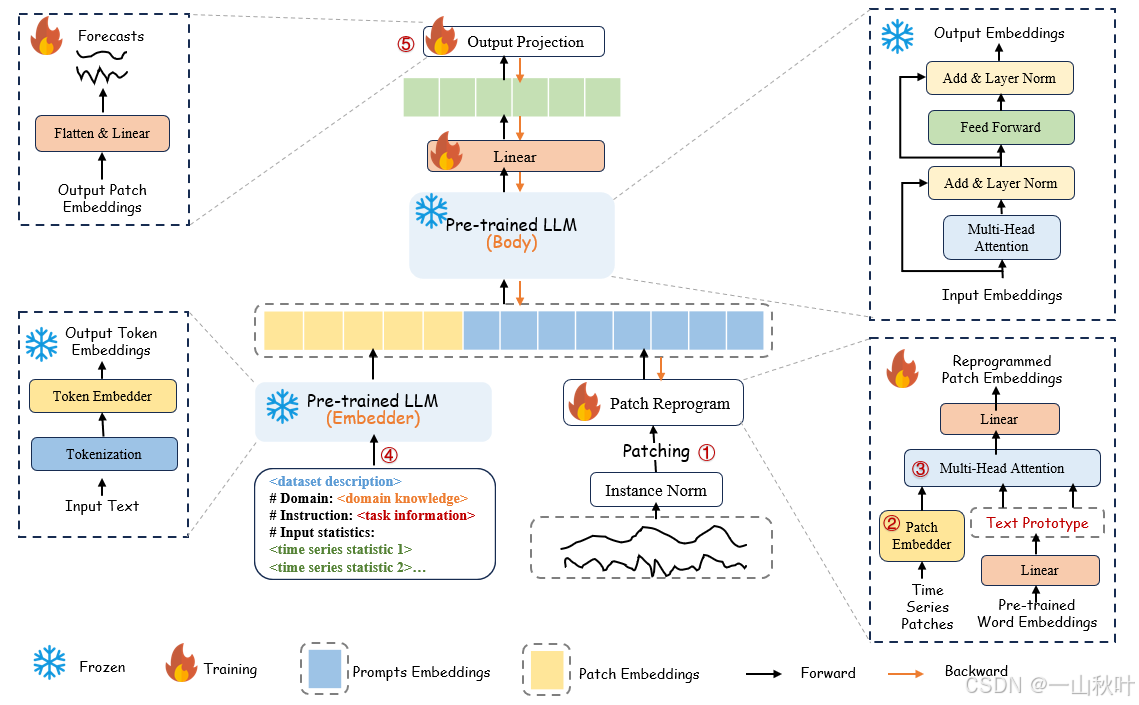
更多推荐

UFW防火墙安全指南

UFW（Uncomplicated Firewall）是Ubuntu/Debian系统中简化防火墙管理的工具，通过直观命令帮助用户有效控制网络流量，提升系统安全性。文章详细介绍了UFW的基本命令，包括启停防火墙、添加规则、限制连接速率和日志配置等操作，并提供了安全最佳实践，如默认拒绝策略、IP地址限制和服务级规则管理。同时，还涵盖高级配置技巧，例如多网络接口设置、规则优先级调整、IPv6支持及与f