SageFormer: Series-Aware Framework for Long-Term Multivariate Time Series Forecasting论文笔记
SageFormer通过结合图神经网络和Transformer架构,提出了一种新颖的系列感知框架,能够有效捕捉多变量时间序列中的序列内和序列间依赖关系。实验结果表明,SageFormer在多个数据集上均显著优于现有的最先进模型,尤其是在处理大规模数据集时表现出色。未来的研究可以进一步优化模型的计算效率、增强图结构的可解释性,并提升模型在处理极端事件和跨领域数据时的泛化能力。
基本信息
发表刊物
IEEE internet of things journal
发表年份
2024
作者
张振伟,孟凌航,顾远涛
第一完成单位(国内)
清华大学
论文内容
解决的问题
1、如何有效表示不同时间序列之间的多样化时间模式
-
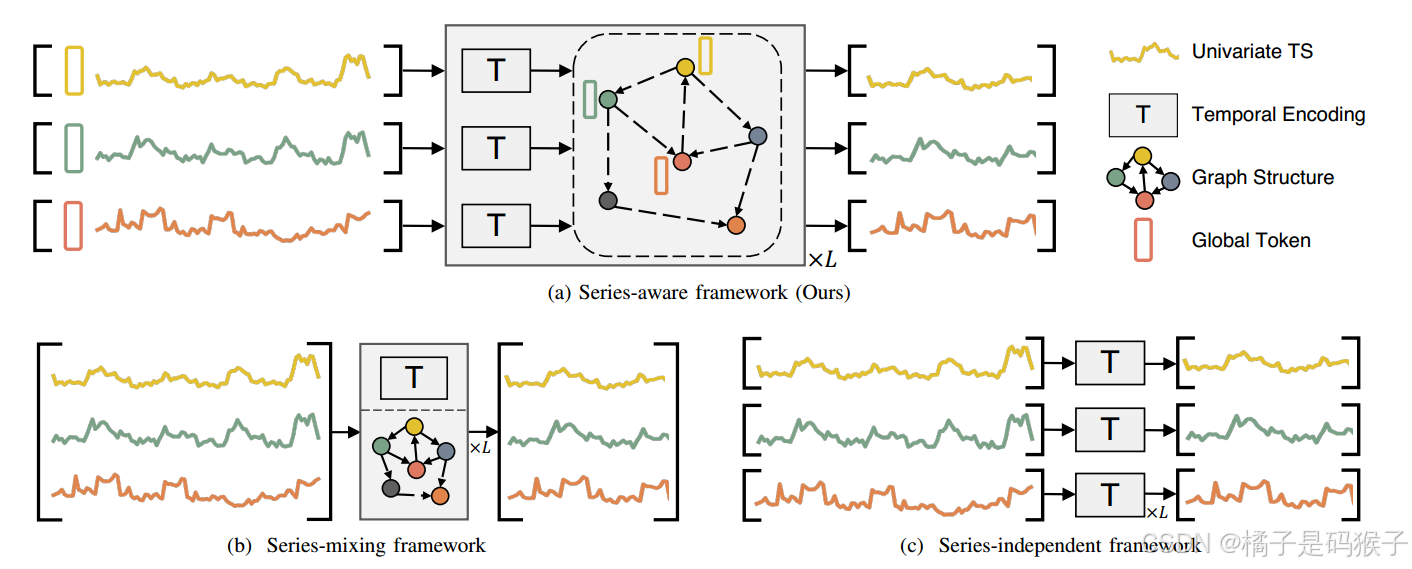
传统基于Transformer模型主要关注时间依赖性,通常使用线性转换将不同的序列合并到隐藏的时间嵌入中,称为“序列混合框架”,序列间依赖关系没有显式建模,导致信息提取效率低下。
-
近期研究发现,有意排除序列间依赖关系的模型(称为“序列独立框架”)可以产生显著改善的预测结果,因为能够减少模型对数据分布的敏感性,从而增强模型对分布漂移的鲁棒性。然而,对于某些数据集,这种方法可能不是最优的,因为它完全忽略了序列间的依赖关系。
这强调了在建模内部和序列间依赖关系时需要的复杂平衡,标志着它是MTS预测研究的关键领域。
论文提出序列感知框架(series-aware framework),通过引入全局可交互的全局标记(global tokens),捕捉每个变量的全局信息,并通过序列内和序列间的交互来增强模型对多样化时间模式的表示能力。
2、如何避免跨序列的冗余信息影响
-
时间序列分析中,冗余信息主要表现为时间冗余和序列冗余。
-
时间冗余指的是单个序列中的重复模式(如周期性或季节性),这些模式不会为预测增加新的信息;
-
而序列冗余指的是多个序列之间,由于它们之间的相关性或共运性,而显现出的相似模式。
-
论文提出使用稀疏连接的图结构来减少序列维度上的冗余信息,并通过全局标记来封装和减轻时间维度上的冗余影响。这种方法能够有效处理低秩数据集中的冗余问题,并在序列数量增加时保持稳定的性能。
解决问题的方法
序列感知框架(Series-Aware Framework)

-
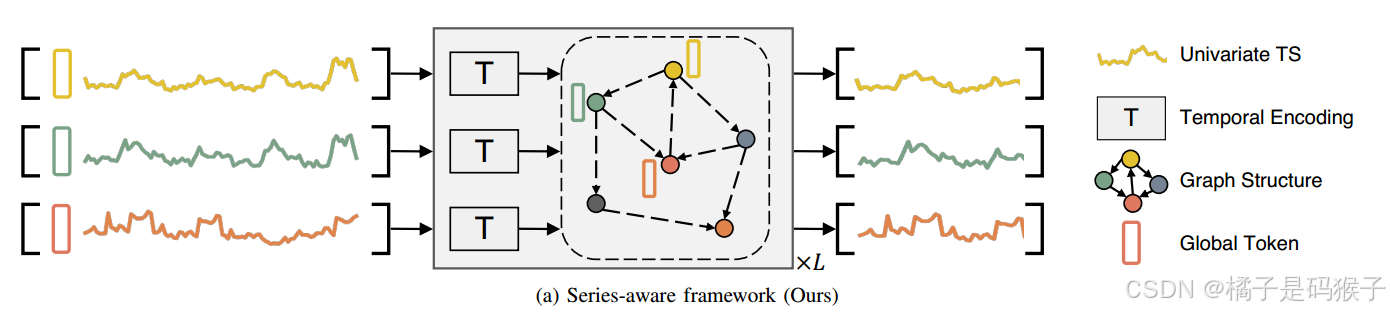
系列感知框架主要包括以下两个关键组件:
-
全局标记生成(Global Tokens Generation)
-
迭代消息传递(Iterative Message Passing)
迭代消息传递中,当前架构可用于序列间和序列内的信息传播(结合图1a来看,实际上就是在每一层进行图聚合和时间编码)。
-
-
最后使用一个线性解码器头来生成预测结果。
SageFormer
SageFormer是系列感知框架的一个实例,使用GNN来建模系列间的依赖关系,同时利用Transformer来捕获系列内的依赖关系,同时减少冗余信息的影响。
输入处理与全局标记(Series-aware Global Tokens)
-
输入处理
-
根据PatchTST,输入MTS:
$$
X∈R^{C×H}
$$(C 是序列的数量,H 是历史时间步长)被分割成重叠的片段(patches):
$$
X_{p}=\{X_1+X_2+...+X_C\}∈R^{C×N×P}
$$N = ⌊(H − P)/S⌋ + 2
(每个片段的长度为 P,N是Patch数,S表示相邻patch之间的不重叠长度)
-
每一个系列 c 对应Patch片段
$$
X_c = {x^1_c, ···,x^N_c }∈R^{N×P}
$$通过可训练的线性投影
$$
E_{proj} ∈ R^{P×D_h}
$$映射到大小为Dh的一致潜在空间,生成嵌入表示。
-
-
全局标记
-
在每个序列的输入前添加 M 个可学习的全局标记
$$
g_1,g_2,...,g_M∈R^{D_h}
$$其中 Dh 是隐藏层维度。
-
全局标记是随机初始化的,并通过训练逐步优化;作用是捕捉每个序列的全局信息,并通过序列内和序列间的交互来增强模型的表示能力。
-
-
输入嵌入
最终的输入嵌入由全局标记和序列片段组成:
$$
X^{(0)}∈R^{C×(M+N)×D_h}
$$其中
$$
X_{c,:,:}^{(0)}=[g_1;…;g_M;x_c^1E_{proj};…;x_c^NE_{proj}]+E_{pos}
$$位置信息通过1D可学习加性位置嵌入Epos增强。
图结构学习(Graph Structure Learning)
-
图结构的表示
-
节点和边:
-
在多变量时间序列中,每个序列被视为图中的一个节点,节点之间的边表示序列间的依赖关系。
-
图的邻接矩阵 :
$$
A∈R^{C×C}
$$表示序列间的依赖强度,其中 C 是序列的数量。
-
-
-
图结构的学习
-
节点嵌入:
-
每个序列的节点嵌入通过随机初始化得到,表示为
$$
E∈R^{C×D_g},\\ 其中D_g是节点嵌入的维度
$$
-
-
邻接矩阵的生成:
通过下面公式生成邻接矩阵:
$$
M_1=act(EΘ_1),M_2=act(EΘ_2)\ \ (1)\\ A^{'}=ReLU(M_1M_2^T-M_2M_1^T)\ \ (2)\\ 其中Θ_1,Θ_2∈R^{D_g×D_g}是可训练的参数矩阵,act是非线性激活函数,A^{'}是初步的邻接矩阵,表示序列间的依赖关系。
$$按照MTGNN的方法,采用(2)学习单向依赖关系
-
稀疏化处理:
-
为减少冗余信息,SageFormer对邻接矩阵进行稀疏化处理,只保留每个节点的top-K最近邻居,其余边的权重设为0
-
最终得到的稀疏邻接矩阵 A 用于图神经网络的消息传递
-
-
迭代消息传递(Iterative Message Passing)
嵌入标记由SageFormer编码器层处理,迭代进行时间编码和图形聚合:
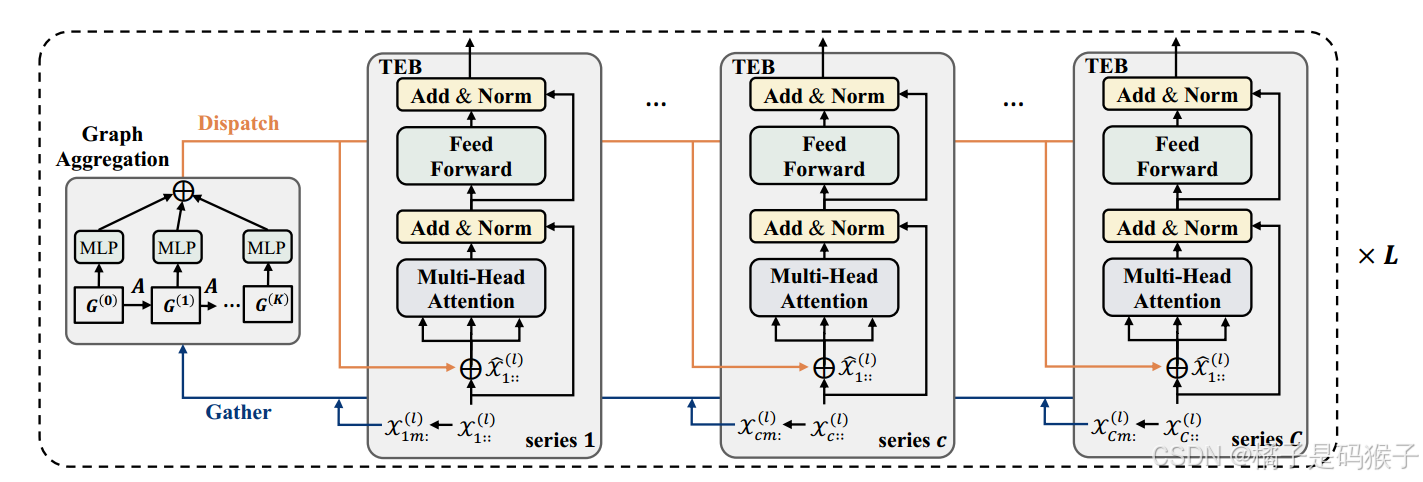
在每个系列中的所有标记之间传播在GNN阶段收集的全局信息,通过迭代消息传递捕获序列内和序列间的依赖关系。
-
图聚合(Graph Aggregation)
图聚合阶段的目的是将每个序列的信息与相邻序列的信息融合,从而增强每个序列的相关模式表示。
-
全局标记的收集
$$
在每一层 l中,首先从所有序列中收集全局标记 \\ G_i^{l}∈R^{C×D_h} ←X_{,:i:,}^{(l)}\\ 其中,C 是序列的数量,D_h是隐藏层维度。i≤M,表示第i个全局标记。
$$-
$$
全局标记是通过前一层的输出嵌入X^{l}提取的,具体来说,取每个序列的前M个嵌入作为全局标记。
$$
-
图聚合的实现
-
使用图神经网络(GNN)对全局标记进行多跳聚合:
$$
\hat{G_i}=\sum_{d=0}^{D}\hat{A^d}G_iW_d \\ \hat{A}是图的拉普拉斯矩阵,表示序列间的依赖关系;\\ W_d是每一跳的可训练权重矩阵,用于对特征向量进行变换和缩放;\\ D是图聚合的深度,表示信息在图中传播的跳数。
$$-
多跳聚合的作用:
通过多跳聚合,模型能够从不同尺度的邻居节点中捕捉信息,从而增强对序列间依赖关系的建模能力。
-
-
信息分发
$$
聚合后的全局标记\hat{G_i}被分发回各自的序列,并与序列的局部标记拼接,形成图增强的嵌入\hat{X^{(l)}}。
$$
-
-
时间编码(Temporal Encoding)
-
Transformer编码器块
-
$$
图增强的嵌入\hat{X^{(l)}}通过Transformer编码器块进行时间编码,捕捉序列内的时间依赖关系
$$ -
Transformer编码器块包括多头自注意力机制和前馈神经网络。
-
-
信息传播
-
通过自注意力机制,全局标记中的信息被传播到序列的局部标记中,从而增强序列内的时间模式表示。
-
-
-
迭代过程
-
图聚合和时间编码在每一层中交替进行,通过多层迭代,模型能够逐步捕捉序列内和序列间的复杂依赖关系。
-
预测头(Forecasting Head)
-
线性解码器:
-
在编码器层的最后,使用一个线性解码器头来生成预测结果。
-
线性解码器的设计简化了模型的计算复杂度,同时保持了较高的预测精度。
-
实验内容
数据集
使用了六个真实世界的数据集和两个合成数据集来验证模型的性能,数据集涵盖了不同的领域和应用场景,能够全面评估模型在长期多变量时间序列(MTS)预测任务中的表现。
真实世界数据集

其中Traffic和Electricity具有更多的变量,可以更好地反映所提出方法的有效性。
合成数据集
Baseline
将SageFormer与九种流行的长期MTS预测问题模型作为基线进行比较,包括:
-
三种明确利用序列间依赖关系的模型:Crossformer , MTGNN和LSTnet ;
-
两个系列无关的神经模型:DLinear和PatchTST ;
-
四种基于Transformer的系列混合模型:Transformer,Informer,Autoformer 和 Non-stationary Transformer
将所有模型的回顾窗口标准化为ILI数据集的36个,其余数据集的96个,以确保公平比较。
实验细节
评价指标
MAE和MSE
实验设置
-
为了确保实验结果的可靠性,每个实验在NVIDIA TITAN RTX 3090 24GB GPU上运行五次,并取平均值以减少随机波动的影响。
优化策略
-
优化目标是最小化均方误差(MSE)
-
使用Adam优化器进行优化,学习率设置为1e-4
-
模型训练大约进行20个epoch,并使用早停机制(early stopping)来防止过拟合
模型架构与超参数
-
编码器层数:
-
默认SageFormer包含2个编码器层。对于较大的数据集(如Traffic和Electricity),使用3个编码器层以增强模型的表达能力。
-
-
注意力头数:
-
多头自注意力机制中的注意力头数设置为16。
-
-
隐藏层维度:
-
模型的隐藏层维度 Dh 设置为512。
-
-
全局标记数量:
-
全局标记的数量 M 设置为1。
-
-
节点嵌入维度:
-
节点嵌入的维度 Dg 设置为16。
-
-
最近邻居数量:
-
图结构中的每个节点的最近邻居数量 K 设置为16。
-
-
图聚合深度:
-
图聚合的深度 D 设置为3,表示信息在图中传播的跳数。
-
-
片段长度与步长:
-
片段长度 P 设置为24,步长 S 设置为8,与PatchTST模型保持一致,确保模型能够捕捉局部时间模式。
-
实验结果
主要结果
-
长期预测结果
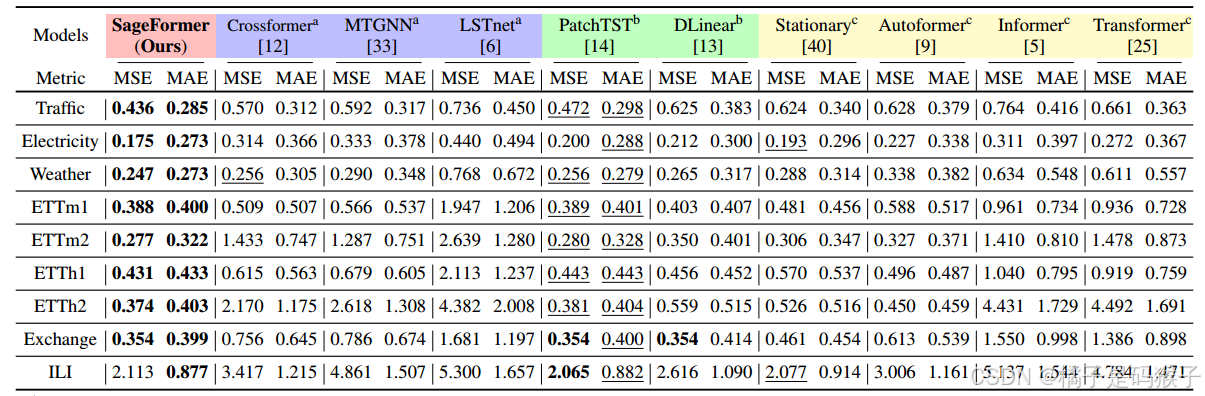
-
SageFormer在所有数据集和预测长度上均表现出色,尤其是在Traffic和Electricity这两个具有更多变量的数据集上最为显著
-
在Traffic数据集上,SageFormer的平均MSE比之前的最优模型降低了7.4%(从0.471降至0.436)。
-
在Electricity数据集上,SageFormer的平均MSE比之前的最优模型降低了9.3%(从0.193降至0.175)。
-
-
框架通用性
系列感知框架可作为基于Transformer的体系结构的通用扩展,将SageFormer框架应用于三个突出的Transformer方法:
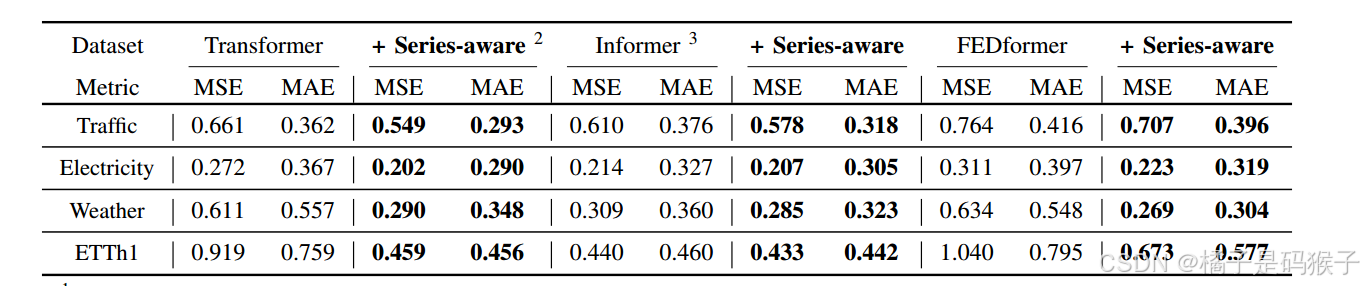
-
论文方法持续提高了不同模型的预测能力,表明所提出的系列感知框架是一个有效的,普遍适用的框架
-
通过利用图结构,它可以更好地利用序列内和序列间的依赖关系,最终实现卓越的预测性能
-
消融实验
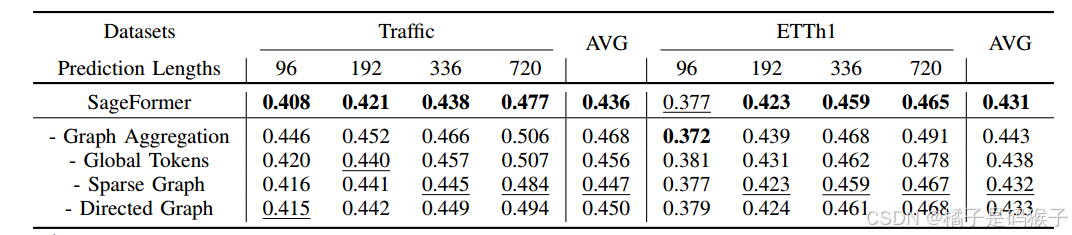
-
图聚合模块的影响
移除SageFormer中的图聚合模块,预测精度大幅下降:
-
在Traffic数据集上,移除图聚合模块后,模型的平均MSE增加了7.3%。
-
在ETTh1数据集上,移除图聚合模块后,模型的平均MSE增加了2.8%。
-
结果表明,图聚合模块对提升模型性能至关重要,尤其是在序列数量较多的数据集上。
-
-
全局标记的影响
序列感知的全局标记增强了模型的预测精度,同时也减少了计算开销。
如果所有标记(不仅仅是全局标记)都参与图传播计算,在Traffic和ETTh1数据集上的性能将分别下降6.3%和1.6%。
-
稀疏约束和有向图构造
-
对于更大的数据集更有效,相比之下对较小的数据集的预测结果几乎没有影响。
-
表明,应用稀疏约束可以减轻变量冗余对模型的影响,同时节省计算资源。
-
超参数的影响
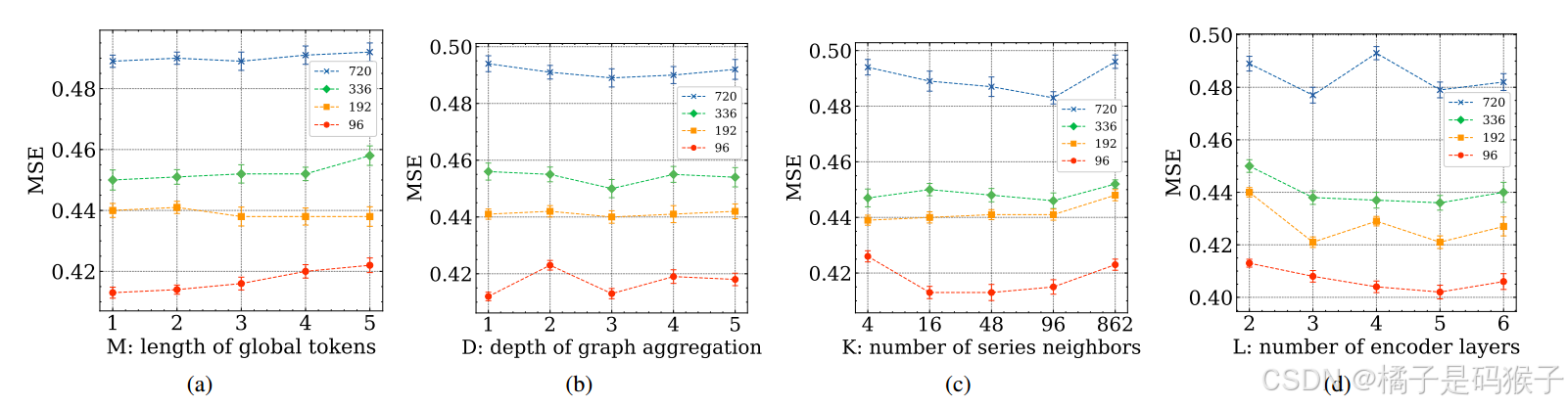
-
全局标记长度(M)
-
模型性能对全局标记长度的变化不敏感,设置 M=1 即可获得较好的性能。
-
-
图聚合深度(D)
-
图聚合深度对模型性能有一定影响,设置 D 能够在准确性和效率之间取得平衡。
-
-
最近邻居数量(K)
-
较大的 K 值通常能带来更好的性能,但完全连接的图会导致性能下降,因此设置 K=16。
-
-
编码器层数(L)
-
增加编码器层数会提高模型的参数量和计算时间,但超过3层后性能提升不明显,因此设置 L=3。
-
重新审视全局标记长度:
挑战了更多的全局标记总是提高模型性能的假设。
与预期相反,增加全局标记长度与改善的结果并不线性相关,可以归因于,单个全局标记在捕获必要的序列内交互方面的有效性。从本质上讲,一个全局标记通常足以封装密钥系列信息——在有效的情况下,更简单的解决方案更可取。
因此,使用单个全局令牌来优化模型,平衡效率和性能。
合成数据集实验
合成数据集
-
有向图循环数据集
-
数据集包含10个时间序列,每个序列的长度为10,000。
-
每个时间序列的值由其前一个序列的值生成,形成一个有向循环图结构。
-
生成公式:
$$
x_{i,t}∼N(\beta x_{(i-1\ mod\ N),t-10},\sigma^{2})\\ 其中,x_{i,t}是第i个变量t时刻的值;\beta是缩放因子,\sigma^{2}是方差,10是滞后时间
$$ -
特点:数据集具有明确的有向循环图结构,适合评估模型对序列间依赖关系的建模能力。
-
-
Low-rank Dataset(低秩数据集)
-
数据集由多个时间序列组成,每个序列的长度为10,000。
-
每个序列的值由多个正弦波的加权组合生成,并加入高斯噪声。
-
生成公式:
$$
x_{i}=\sum_{m=1}^{M}B_{i,m}sin(2\piω_{⌊i/K⌋,m}t)+\epsilon_{i,t}\\ 其中,B_{i,m}是权重,ω_{⌊i/K⌋,m}是频率,\epsilon_{i,t}是高斯噪声。
$$ -
特点:数据集具有低秩特性,适合评估模型对冗余信息的处理能力。
-
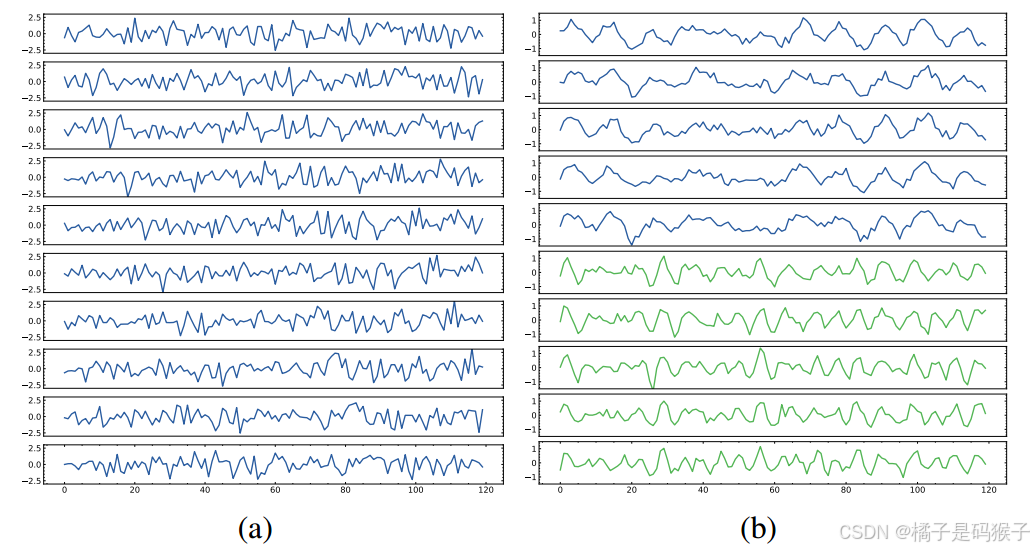
实验结果
-
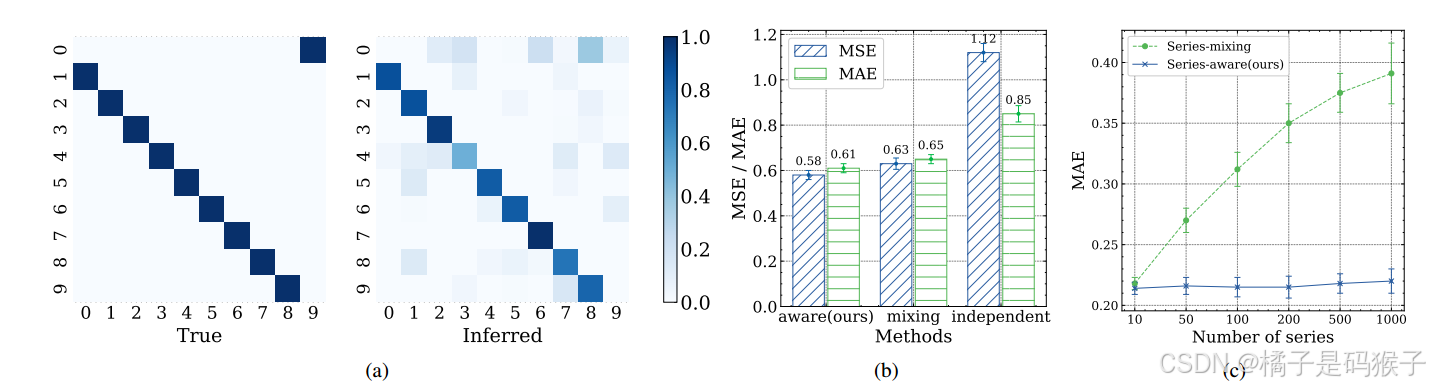
序列相关性推断 图(a)
将实际的序列间关系与SageFormer模型的推断结果并列,强调了SageFormer在恢复这些联系方面的熟练程度。
-
有向循环数据集结果 图(b)
-
SageFormer在预测任务中表现最佳,MSE和MAE均显著低于其他模型。
-
序列独立的模型在该数据集上表现较差,MSE超过1,表明其无法有效捕捉序列间的依赖关系。
-
-
低秩数据集结果 图(c)
-
SageFormer在低秩数据集上表现稳定,随着序列数量的增加,其预测性能没有显著下降。
-
序列混合的模型在序列数量增加时性能迅速下降,表明其无法有效处理冗余信息。
-
图结构的有效性和稳定性
-
图结构的有效性
-
SageFormer能够从数据中准确推断出图结构,尤其是在有向循环图数据集上,模型推断的图结构与真实结构高度一致。
-
-
图结构的稳定性
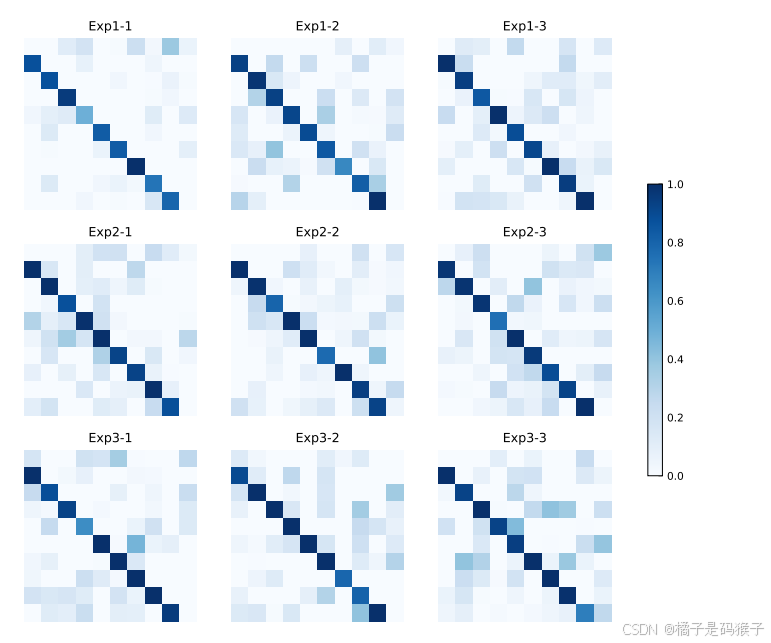
在三个独立试验中为三个不同的数据集生成可视化:
-
通过多次随机实验,SageFormer推断的图结构在不同实验之间保持高度一致,表明其具有较好的稳定性。
-
全局标记的讨论
Transformer注意力权重可视化
-
实验设置:
-
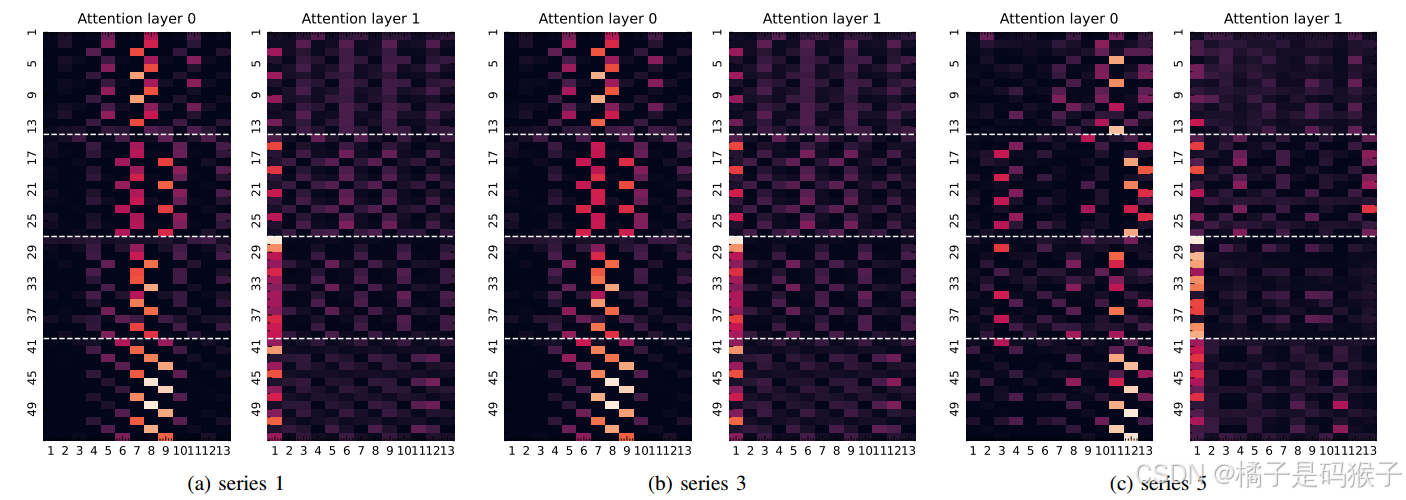
对模型在ETTh1数据集上的Transformer注意力权重进行可视化,重点关注全局标记与其他时间标记之间的注意力分布。
-
-
结果分析:
-
在第一层,全局标记的注意力权重较低,因为全局标记是随机初始化的,尚未捕捉到序列的全局信息。
-
在第二层,全局标记的注意力权重显著增加,表明全局标记通过图神经网络(GNN)传播的信息开始发挥作用,能够有效捕捉序列间的依赖关系。
-
结果表明,全局标记在模型的前几层中逐渐学习到序列的全局信息,并通过自注意力机制将信息传播到其他时间标记中。
-
全局标记的可视化
-
实验设置:
-
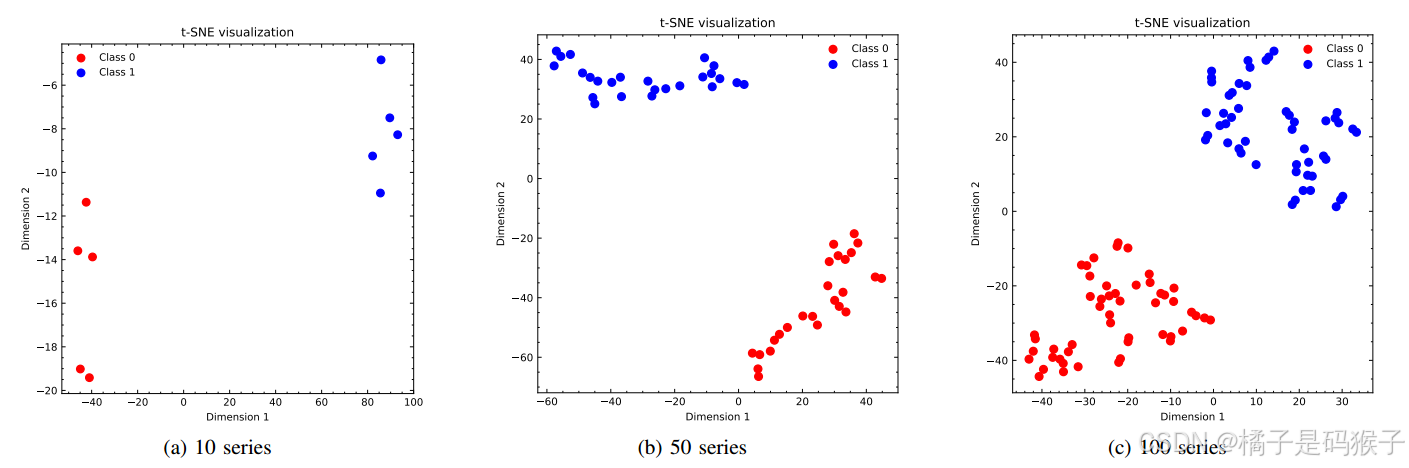
在低秩数据集上对全局标记进行了可视化,并使用t-SNE将全局标记的嵌入投影到二维空间。

-
-
结果分析:
-
全局标记在低秩数据集上表现出明显的分组结构,反映了数据集中的低秩特性;
-
在10个变量的低秩数据集上,全局标记被清晰地分为两组,表明全局标记能够有效捕捉序列间的依赖关系;
-
在50个和100个变量的低秩数据集上,全局标记依然表现出明显的分组结构,验证了全局标记处理多变量时间序列时的有效性。
-
全局标记的作用总结
-
序列内依赖:
-
通过自注意力机制捕捉每个序列的全局信息,例如长期趋势或周期性模式;
-
-
序列间依赖:
-
通过图神经网络(GNN)进行信息传递,捕捉序列间的依赖关系;
-
-
减少冗余:
-
全局标记能够封装序列的全局特征,减少时间维度上的冗余信息。
-
计算效率分析

计算复杂度
-
编码器部分:
-
理论上计算复杂度为 O(T2),其中T 是历史序列长度;但由于使用了较大的片段长度 P,实际运行时间接近线性复杂度
-
额外的 O(C2)复杂度是标准的图卷积操作,其中 C 是序列数量,通过稀疏化处理,复杂度可以进一步降低。
-
-
解码器部分:
-
SageFormer使用线性解码器头,复杂度为 O(T),显著降低了计算开销。
-
运行时间和内存消耗
-
实验设置:
-
在Traffic数据集上比较了SageFormer与其他Transformer-based模型的运行时间和内存消耗。
-
-
结果分析:
-
SageFormer的运行时间为 0.31±0.03秒/批次,内存消耗为12.42 GB。
-
与PatchTST相比,SageFormer的运行时间稍慢,但显著快于Crossformer。
-
结果表明,SageFormer在计算效率和预测精度之间取得了良好的平衡。
-
计算效率总结
-
优势:
-
SageFormer通过稀疏化处理和线性解码器头,显著降低了计算复杂度。
-
在实际运行中,SageFormer的运行时间和内存消耗与其他Transformer-based模型相当,表现出较高的计算效率。
-
-
改进空间:
-
未来可以通过进一步优化图聚合部分的计算复杂度,提升模型的计算效率。
-
未来方向
依赖关系不代表因果关系
-
SageFormer能够捕捉序列间的依赖关系,但这些依赖关系并不一定代表因果关系。由于时间序列数据通常是非平稳的,模型捕捉到的依赖关系在实际应用中可能不可靠。
-
未来改进方向:
-
未来的研究可以尝试引入因果推理机制,使模型能够学习到序列间的因果关系,从而提高预测的可靠性。
-
图结构的可解释性
-
SageFormer通过图结构学习序列间的依赖关系,但这些图结构的可解释性较差。模型推断出的图结构可能难以直观理解,尤其是在复杂的多变量时间序列数据中。
-
未来改进方向:
-
未来的研究可以尝试增强图结构的可解释性,例如通过可视化工具或引入领域知识来辅助解释图结构。
-
模型复杂度
-
SageFormer结合了图神经网络(GNN)和Transformer架构,虽然通过稀疏化处理和线性解码器头降低了计算复杂度,但模型的整体复杂度仍然较高,尤其是在处理大规模数据时。
-
未来改进方向:
-
未来的研究可以进一步优化模型的计算效率,例如通过更高效的图卷积算法或模型压缩技术来减少计算开销。
-
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容







所有评论(0)