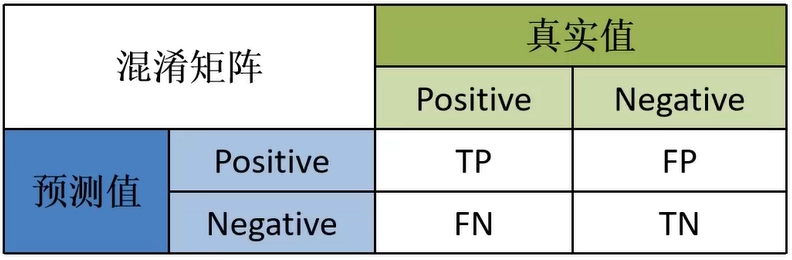
混淆矩阵 confusion matrix

True Positive (TP):

模型将实际为正类别的样本正确预测为正类别 --- 真正的正类 ---> 实际上是一个正类

False Positive (FP):

模型将实际为负类别的样本错误预测为正类别 --- 虚假的正类 ---> 实际上是一个负类

True Negative (TN)

模型将实际为负类别的样本正确预测为负类别 --- 真正的负类 ---> 实际上是一个负类

False Negative (FN)

模型将实际为正类别的样本错误预测为负类别 --- 虚假的负类 ---> 实际上是一个正类

---

考虑一个简单的二元分类问题，假设开发了一个垃圾邮件检测器，目标是将电子邮件分为两类：垃圾邮件（正类别）和非垃圾邮件（负类别）

	预测为垃圾邮件（预测为正类）	预测为非垃圾邮件（预测为负类）
实际是垃圾邮件（正类）	60 (TP)	10 (FN)
实际是垃圾邮件（正类）	5 (FP)	25 (TN)

TP = 60 --- 60个真正的正类 ---> 模型将60封实际是垃圾邮件的邮件预测为垃圾邮件

FP = 5 --- 5个虚假的正类 ---> 模型将5封实际上不是垃圾邮件的邮件错误地预测为垃圾邮件

TN = 25 --- 25个真正的负类 ---> 模型将25封实际上不是垃圾邮件的邮件正确预测为非垃圾邮件

FN = 10 --- 5个虚假的负类 ---> 模型将5封实际上不是垃圾邮件的邮件错误地预测为垃圾邮件

---

已知：医院有100个人，其中20个人有癌症，80个人无癌症
目标：现在要找出所有有癌症的人
结果：选了50人，其中20有癌症，30人无癌症

	预测为有癌症（预测为正类）	预测为无癌症（预测为负类）
实际有癌症（正类）	20 (TP)	0 (FN)
实际无癌症（负类）	30 (FP)	50 (TN)

找癌症 ---> 癌症视为正类 ---> 无癌症视为负类

找到50个 ---> 50个正类 ---> 50个负类

50个正类里，20个真正类 ---> TP = 20

50个正类里，30个假正类 ---> NP = 30

50个负类里，50个真负类 ---> TN = 50

50个负类里，0个假负类 ---> NP = 0