S变换（S-Transform）的数学理论详解

引言

S变换（S-Transform）是由加拿大学者Stockwell等人于1996年提出的一种时频分析方法，它巧妙地结合了短时傅里叶变换（STFT）的相位特性和连续小波变换（CWT）的多分辨率分析能力。S变换既保留了与傅里叶变换直接联系的绝对相位信息，又具备小波变换随频率变化的分辨率特性，因此得到了广泛应用。

基本原理

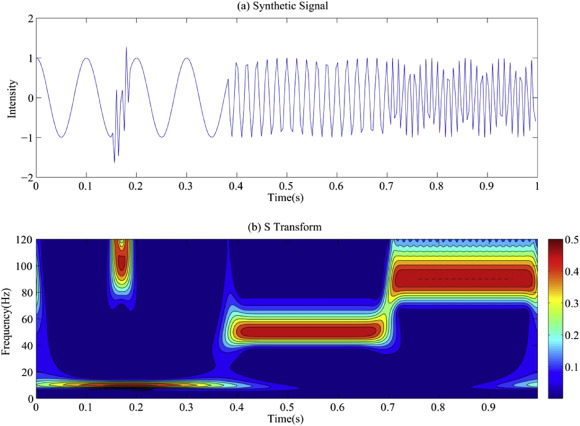
S变换可以看作是短时傅里叶变换的一种扩展，其核心思想是使用高斯窗函数作为基本窗口，但窗口宽度会随着频率自适应调整。低频成分使用宽窗口以获得更好的频率分辨率，高频成分则使用窄窗口以获得更好的时间分辨率。这种自适应性使S变换非常适合分析非平稳信号，尤其是那些同时包含高频和低频成分的复杂信号。

从概念上讲，S变换融合了两个重要的信号分析工具：短时傅里叶变换提供了与时间有关的频率信息，小波变换则提供了多尺度分析能力。S变换可以看作是"相位修正的连续小波变换"，也可以看作是"频率依赖的短时傅里叶变换"。

一、基本定义与数学表达

S变换作为一种时频分析工具，其严格的数学定义源于连续小波变换与短时傅里叶变换的理论基础。

连续S变换的定义

对于一维时间信号 $h(t)$，其连续S变换定义为：

$$S(\tau ,f)={\int }_{-\infty }^{\infty }h(t)\cdot \frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}}\cdot e^{-i2\pi ft}dt$$

这里 $\tau$ 表示时间定位参数，$f$ 表示频率参数，指数函数 $e^{-\frac{(t-\tau {)}^2{f}^2}{2}}$ 是频率依赖的高斯窗函数，系数 $\frac{|f|}{\sqrt{2\pi }}$ 确保窗函数的能量为常数。更紧凑的形式可表示为：

$$S(\tau ,f)={\int }_{-\infty }^{\infty }h(t)\cdot w(t-\tau ,f)\cdot e^{-i2\pi ft}dt$$

其中窗函数为：

$$w(t-\tau ,f)=\frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}}$$

离散S变换的推导

对于离散时间信号 $h[kT]$ (其中 $k=0,1,...,N-1$，$T$ 是采样间隔)，首先计算其离散傅里叶变换：

$$H[n]=\frac{1}{N}\sum _{k=0}^{N-1}h[kT]\cdot e^{-i2\pi nk/N}$$

对于 $n\ne 0$（非零频率），S变换可以表示为：

$$S[jT,\frac{n}{NT}]=\sum _{m=0}^{N-1}H\left[\frac{(m+n)\mathrm{mod}N}{N}\right]\cdot e^{-2{\pi }^2{m}^2/n^2}\cdot e^{i2\pi mj/N}$$

对于 $n=0$（零频率），S变换退化为信号的直流分量：

$$S[jT,0]=\frac{1}{N}\sum _{k=0}^{N-1}h[kT]=H[0]$$

二、S变换的数学性质

2.1 傅里叶变换性质

S变换与傅里叶变换之间存在严格的数学联系。对S变换结果在时间上积分，可得：

$${\int }_{-\infty }^{\infty }S(\tau ,f)d\tau =H(f)={\int }_{-\infty }^{\infty }h(t)e^{-i2\pi ft}dt$$

证明过程涉及窗函数的性质：

$${\int }_{-\infty }^{\infty }\frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}}d\tau =1$$

将此代入S变换定义：

$$\begin{array}{rl}{\int }_{-\infty }^{\infty }S(\tau ,f)d\tau & ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }h(t)\cdot \frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}}\cdot e^{-i2\pi ft}dtd\tau \\ & ={\int }_{-\infty }^{\infty }h(t)\cdot e^{-i2\pi ft}\left({\int }_{-\infty }^{\infty }\frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}}d\tau \right)dt\\ & ={\int }_{-\infty }^{\infty }h(t)\cdot e^{-i2\pi ft}dt=H(f)\end{array}$$

2.2 逆S变换公式

S变换的可逆性通过以下复杂积分公式体现：

$$h(t)={\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^{\infty }S(\tau ,f)d\tau \right)e^{i2\pi ft}df$$

证明可通过代入S变换的定义实现：

$$\begin{array}{rl}{\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^{\infty }S(\tau ,f)d\tau \right)e^{i2\pi ft}df& ={\int }_{-\infty }^{\infty }H(f)e^{i2\pi ft}df\\ & ={\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^{\infty }h(t^{\prime })e^{-i2\pi f{t}^{\prime }}d{t}^{\prime }\right)e^{i2\pi ft}df\\ & ={\int }_{-\infty }^{\infty }h(t^{\prime })\left({\int }_{-\infty }^{\infty }{e}^{i2\pi f(t-t^{\prime })}df\right)d{t}^{\prime }\\ & ={\int }_{-\infty }^{\infty }h(t^{\prime })\delta (t-t^{\prime })d{t}^{\prime }=h(t)\end{array}$$

其中利用了狄拉克函数性质 ${\int }_{-\infty }^{\infty }{e}^{i2\pi f(t-t^{\prime })}df=\delta (t-t^{\prime })$。

2.3 时频分辨率理论

S变换的时频分辨率以海森堡不确定性原理为基础，可通过窗函数的标准差来量化：

时间分辨率为：

$$\Delta t(f)=\frac{{\sigma }_t}{|f|}=\frac{1}{|f|\sqrt{2}}$$

频率分辨率为：

$$\Delta f(f)=\frac{{\sigma }_f|f|}{2\pi }=\frac{|f|}{2\pi \sqrt{2}}$$

其中 ${\sigma }_t$ 和 ${\sigma }_f$ 是标准高斯窗的时间和频率标准差：

$${\sigma }_t^2=\frac{{\int }_{-\infty }^{\infty }{t}^2{e}^{-t^2}dt}{{\int }_{-\infty }^{\infty }{e}^{-t^2}dt}=\frac{1}{2}$$

$${\sigma }_f^2=\frac{{\int }_{-\infty }^{\infty }{f}^2|G(f){|}^{2}df}{{\int }_{-\infty }^{\infty }|G(f){|}^{2}df}=\frac{1}{2}$$

其中 $G(f)$ 是高斯窗的傅里叶变换。

2.4 能量守恒定理

根据Parseval定理，S变换满足能量守恒关系：

$${\int }_{-\infty }^{\infty }|h(t){|}^{2}dt={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }|S(\tau ,f){|}^2\frac{d\tau df}{|f|}$$

证明涉及到使用复杂的内积运算和变换域的性质。

三、高级S变换变体的数学表达

3.1 广义S变换

广义S变换引入了控制参数 $\alpha$ 和 $\beta$，使得窗函数更加灵活：

$$w(t-\tau ,f,\alpha ,\beta )=\frac{|f{|}^{\alpha }}{\beta \sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^{2\alpha }}{2{\beta }^2}}$$

相应的广义S变换定义为：

$$S(\tau ,f,\alpha ,\beta )={\int }_{-\infty }^{\infty }h(t)\cdot \frac{|f{|}^{\alpha }}{\beta \sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^{2\alpha }}{2{\beta }^2}}\cdot e^{-i2\pi ft}dt$$

当 $\alpha =1$ 和 $\beta =1$ 时，退化为标准S变换。

3.2 分数阶S变换

分数阶S变换将整数阶傅里叶变换替换为分数阶傅里叶变换：

$$S_{\gamma }(\tau ,f)={\int }_{-\infty }^{\infty }h(t)\cdot \frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}}\cdot e^{-i2\pi f(t-\tau {)}^{\gamma }}dt$$

其中 $\gamma$ 是分数阶参数，当 $\gamma =1$ 时退化为标准S变换。

3.3 各向异性S变换

各向异性S变换使用方向依赖的窗函数：

$$S_a(\tau ,f,\theta )={\int }_{-\infty }^{\infty }h(t)\cdot w_a(t-\tau ,f,\theta )\cdot e^{-i2\pi ft}dt$$

其中 $w_a$ 是各向异性窗函数：

$$w_a(t-\tau ,f,\theta )=\frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}(1+ϵ\cos (\theta -\varphi ))}$$

参数 $ϵ$ 控制各向异性程度，$\theta$ 和 $\varphi$ 分别是分析方向和信号局部方向。

四、多维S变换的数学理论

4.1 二维S变换

对于二维信号 $h(x,y)$，其二维S变换定义为：

$$S(x,y,f_x,f_y)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }h(x^{\prime },y^{\prime })\cdot w(x^{\prime }-x,y^{\prime }-y,f_x,f_y)\cdot e^{-i2\pi (f_x{x}^{\prime }+f_y{y}^{\prime })}d{x}^{\prime }d{y}^{\prime }$$

其中二维高斯窗函数为：

$$w(x^{\prime }-x,y^{\prime }-y,f_x,f_y)=\frac{|f|}{2\pi }{e}^{-\frac{(x^{\prime }-x{)}^2{f}_x^2+(y^{\prime }-y{)}^2{f}_y^2}{2}}$$

其中 $|f|=\sqrt{f_x^2+f_y^2}$ 是频率的模。

4.2 多维S变换公式

对于N维信号 $h(\mathbf{r})$，其中 $\mathbf{r}=(r_1,r_2,...,r_N)$，多维S变换定义为：

$$S(\mathbf{r},\mathbf{f})={\int }_{{\mathbb{R}}^N}h({\mathbf{r}}^{\prime })\cdot w({\mathbf{r}}^{\prime }-\mathbf{r},\mathbf{f})\cdot e^{-i2\pi \mathbf{f}\cdot {\mathbf{r}}^{\prime }}d{\mathbf{r}}^{\prime }$$

其中N维高斯窗函数为：

$$w({\mathbf{r}}^{\prime }-\mathbf{r},\mathbf{f})=\frac{|\mathbf{f}|}{(2\pi {)}^{N/2}}{e}^{-\frac{|\mathbf{f}{|}^2|{\mathbf{r}}^{\prime }-\mathbf{r}{|}^2}{2}}$$

其中 $|\mathbf{f}|=\sqrt{{\sum }_{i=1}^N{f}_i^2}$ 和 $|{\mathbf{r}}^{\prime }-\mathbf{r}|=\sqrt{{\sum }_{i=1}^N(r_i^{\prime }-r_i{)}^2}$。

五、信息理论与S变换

5.1 S变换的熵表达

S变换的信息熵可定义为：

$$H_S=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }p(\tau ,f)\log p(\tau ,f)d\tau df$$

其中 $p(\tau ,f)$ 是归一化的S变换能量密度：

$$p(\tau ,f)=\frac{|S(\tau ,f){|}^2}{{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }|S(\tau ,f){|}^{2}d\tau df}$$

5.2 Rényi熵测度

S变换的Rényi熵是一种更一般的信息度量：

$$H_{\alpha }(S)=\frac{1}{1-\alpha }\log \left({\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left[\frac{|S(\tau ,f){|}^2}{{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }|S(\tau ,f){|}^{2}d\tau df}\right]}^{\alpha }d\tau df\right)$$

当 $\alpha \to 1$ 时，Rényi熵趋近于Shannon熵。

六、与小波变换的数学关系

S变换与连续小波变换(CWT)有着严格的数学联系。设 $W(\tau ,d)$ 为使用尺度参数 $d$ 的连续小波变换：

$$W(\tau ,d)={\int }_{-\infty }^{\infty }h(t)\frac{1}{\sqrt{d}}{\psi }^{\ast }\left(\frac{t-\tau }{d}\right)dt$$

若使用Morlet小波作为母小波：

$$\psi (t)=e^{-t^2/2}{e}^{i2\pi f_{0}t}$$

则S变换可表示为：

$$S(\tau ,f)=e^{i2\pi f\tau }\cdot W\left(\tau ,\frac{1}{|f|}\right)\cdot e^{-2{\pi }^2(f_0-f{)}^2/f^2}$$

当 $f_0=0$ 时，简化为：

$$S(\tau ,f)=e^{i2\pi f\tau }\cdot W\left(\tau ,\frac{1}{|f|}\right)$$

这表明S变换是相位修正的连续小波变换。

七、复变函数理论与S变换

将S变换扩展到复频域，可得：

$$S(\tau ,\zeta )={\int }_{-\infty }^{\infty }h(t)\cdot \frac{|\zeta |}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2|\zeta {|}^2}{2}}\cdot e^{-i2\pi \zeta t}dt$$

其中 $\zeta =f+ig$ 是复频率，$g$ 表示衰减因子。

对于复数信号 $h(t)=h_r(t)+i{h}_i(t)$，可定义分析性S变换：

$$S_A(\tau ,f)=S_r(\tau ,f)+i{S}_i(\tau ,f)$$

其中 $S_r$ 和 $S_i$ 分别是实部和虚部信号的S变换。

八、高阶谱分析与S变换

S变换可扩展到高阶谱分析，定义S变换双谱：

$$BS(\tau ,f_1,f_2)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }S(\tau ,f_1)\cdot S(\tau ,f_2)\cdot S^{\ast }(\tau ,f_1+f_2)d\tau$$

类似地，S变换三谱定义为：

$$TS(\tau ,f_1,f_2,f_3)={\int }_{-\infty }^{\infty }S(\tau ,f_1)\cdot S(\tau ,f_2)\cdot S(\tau ,f_3)\cdot S^{\ast }(\tau ,f_1+f_2+f_3)d\tau$$

九、函数空间分析与S变换

9.1 S变换的Hilbert空间表示

将S变换看作是Hilbert空间 $L^2(\mathbb{R})$ 上的算子，可得：

$$S:L^2(\mathbb{R})\to L^2({\mathbb{R}}^2)\text{满足}⟨S[h_1],S[h_2]⟩=⟨h_1,h_2{⟩}_{L^2}$$

其中内积定义为：

$$⟨S[h_1],S[h_2]⟩={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }S[h_1](\tau ,f)\cdot S[h_2{]}^{\ast }(\tau ,f)\frac{d\tau df}{|f|}$$

9.2 框架理论分析

S变换可视为一个冗余框架。对于离散实现，存在常数 $0<A\le B<\infty$ 使得：

$$A\Vert h{\Vert }^2\le \sum _{j=0}^{N-1}\sum _{n=0}^{N-1}|S[j,n]{|}^2\le B\Vert h{\Vert }^2$$

对于所有的 $h\in L^2(\mathbb{R})$，其中 $A$ 和 $B$ 是框架界。

十、数值计算理论

10.1 离散S变换的矩阵表示

离散S变换可表示为矩阵形式：

$$\mathbf{S}=\mathbf{W}\cdot \mathbf{H}$$

其中 $\mathbf{S}$ 是S变换系数矩阵，$\mathbf{H}$ 是信号向量，$\mathbf{W}$ 是变换矩阵，其元素为：

$$W_{j,k}(n)=\frac{1}{N}{e}^{-\frac{2{\pi }^2{k}^2}{n^2}}\cdot e^{i2\pi (j-k)/N}\text{当}n\ne 0$$

10.2 快速算法计算复杂度分析

标准S变换的计算复杂度为 $O(N^2\log N)$，但可通过优化算法降低至 $O(N\log N)$。

一种优化算法的时间复杂度分析如下：

1. FFT计算：$O(N\log N)$
2. 对每个频率点 $f$（共 $N_f$ 个点）：
   a. 计算窗函数：$O(N)$
   b. 频域乘法：$O(N)$
   c. IFFT计算：$O(N\log N)$

总复杂度：$O(N_f\cdot N\log N)$，当 $N_f=O(N)$ 时为 $O(N^2\log N)$。

通过频率合并策略，可将复杂度降至 $O(N{\log }^{2}N)$。

十一、随机过程与S变换

11.1 S变换的统计特性

对于随机过程 $X(t)$，其S变换 $S_X(\tau ,f)$ 的统计特性可通过矩来描述。

期望值为：

$$E[S_X(\tau ,f)]={\int }_{-\infty }^{\infty }E[X(t)]\cdot \frac{|f|}{\sqrt{2\pi }}{e}^{-\frac{(t-\tau {)}^2{f}^2}{2}}\cdot e^{-i2\pi ft}dt$$

自相关函数为：

$$R_{S_X}({\tau }_1,f_1,{\tau }_2,f_2)=E[S_X({\tau }_1,f_1)\cdot S_X^{\ast }({\tau }_2,f_2)]$$

11.2 S变换谱密度分析

对于宽平稳随机过程，S变换的功率谱密度定义为：

$$P_S(\tau ,f)=|S_X(\tau ,f){|}^2$$

其期望值与过程的功率谱密度 $P_X(f)$ 有关：

$$E[P_S(\tau ,f)]={\int }_{-\infty }^{\infty }{P}_X(f^{\prime })\cdot |W(f-f^{\prime },\tau ,f){|}^{2}d{f}^{\prime }$$

其中 $W(f^{\prime },\tau ,f)$ 是窗函数的傅里叶变换：

$$W(f^{\prime },\tau ,f)=\frac{1}{\sqrt{2\pi |f|}}{e}^{-\frac{f^{\prime 2}}{2f^2}}{e}^{-i2\pi f^{\prime }\tau }$$