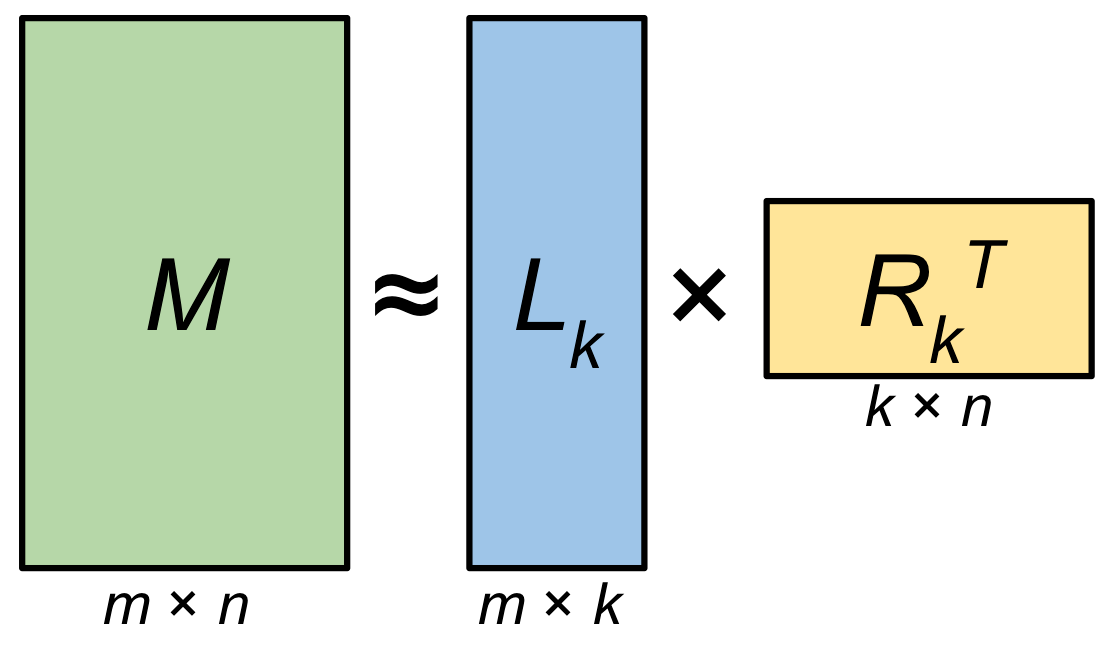
低秩矩阵模型的推导与详解

目录

1. 引言
2. 低秩矩阵的定义
3. 奇异值分解（SVD）与低秩矩阵
   1. Eckart–Young–Mirsky 定理
4. 低秩矩阵模型的常见形式
   1. 矩阵分解模型
   2. 核范数最小化（Nuclear Norm Minimization）
      • 核范数与最小秩的关系
5. 矩阵补全问题示例
   1. Netflix问题
   2. 最优目标与推导
   3. 松弛与等价形式
6. 低秩矩阵求解方法
   1. 软阈值奇异值收缩（SVT）
   2. 交替最小二乘法（ALS）
   3. 梯度方法与凸优化思路
7. 低秩矩阵应用领域
8. 一个简单的Python示例：利用SVD进行低秩近似
9. 总结

---

引言

在数据科学、机器学习和信号处理等众多领域，我们经常面对海量的、高维的矩阵数据。例如：

• 推荐系统：有数百万用户和数十万物品的打分矩阵；
• 图像处理：一张图片可以被看作一个像素矩阵，甚至是三维张量（多通道 RGB）；
• 金融数据：协方差矩阵、时间序列数据等。

这些矩阵往往存在冗余信息或缺失值。低秩矩阵模型 能够有效地利用 “秩小” 这一先验，帮助我们实现降维、去噪、补全数据等重要任务。

---

低秩矩阵的定义

让我们从基本概念开始：设 $M\in {\mathbb{R}}^{m\times n}$ 为一个 $m\times n$ 的实矩阵。其秩（rank） 定义为：
r a n k ( M ) = max ⁡ { k : 存在  k  个线性无关的行向量或列向量 } . \mathrm{rank}(M) = \max \{ k : \text{存在 $k$ 个线性无关的行向量或列向量} \}. rank(M)=max{k:存在 k 个线性无关的行向量或列向量}.

通俗地说，秩可以理解为矩阵真实的“维度”或“复杂度”。当
$$\mathrm{rank}(M)=r\ll \min (m,n)$$
时，我们就称 $M$ 是一个 低秩矩阵（Low-rank Matrix）。

为什么低秩很重要？在数据驱动的场景中，如果矩阵是低秩的，就意味着其中大部分信息可由少数几个“方向”或“基”所刻画。这为我们带来了以下好处：

1. 降维：只需存储或关注这几个主要方向即可；
2. 去噪：在带有噪声的高维数据中，低秩成分往往被看作信号，噪声往往对应高秩或稀疏干扰；
3. 补全：低秩假设下，矩阵的少部分观测值也可能足以推断出矩阵的整体结构。

---

奇异值分解（SVD）与低秩矩阵

对于任何一个矩阵 $M\in {\mathbb{R}}^{m\times n}$，它都可以进行 奇异值分解（Singular Value Decomposition，SVD）。
SVD 的形式可写作：
$$M=U\Sigma V^T,$$
其中：

• $U\in {\mathbb{R}}^{m\times m}$ 是正交矩阵（满足 $U^{T}U=I$），其列向量称为 左奇异向量；
• $V\in {\mathbb{R}}^{n\times n}$ 同样是正交矩阵（满足 $V^{T}V=I$），其列向量称为 右奇异向量；
• $\Sigma \in {\mathbb{R}}^{m\times n}$ 是一个对角矩阵（在非方矩阵时，对角线部分在前面），其对角元素
  $${\sigma }_1\ge {\sigma }_2\ge \dots \ge {\sigma }_{\min (m,n)}\ge 0$$
  称为 奇异值（Singular Values）。

事实上，若 $\mathrm{rank}(M)=r$，则只有前 $r$ 个奇异值为正，其余为零。例如，若 $r\ll \min (m,n)$，你就可以看到 SVD 中出现大量的零奇异值，体现了矩阵的低秩性质。

Eckart–Young–Mirsky 定理

Eckart–Young–Mirsky 定理（也称为矩阵低秩逼近的最优性定理）指出：
给定矩阵 $M$ 的 SVD 为 $M=U\Sigma V^T$。如果我们想要在秩为 $k$ 的所有矩阵中找到与 $M$ 在某种范数下（如弗罗贝尼乌斯范数 $\Vert \cdot {\Vert }_F$）距离最小的矩阵，则该最优解刚好是把 $M$ 的 SVD 中所有奇异值除了最大的 $k$ 个之外全部置零再重构出的矩阵。

用公式表示，当 $\Vert \cdot \Vert$ 为弗罗贝尼乌斯范数 $\Vert \cdot {\Vert }_F$ 时，最优逼近矩阵为
$$M_k=U\mathrm{diag}({\sigma }_1,\dots ,{\sigma }_k,0,\dots ,0)V^T,$$
并且其逼近误差最小。该结果在低秩逼近理论和应用中都非常关键。

---

低秩矩阵模型的常见形式

矩阵分解模型

如果我们明确地假设一个矩阵 $M$ 的秩最多是 $r$，就可以在模型中将 $M$ 表示成如下形式：
$$M=U{V}^T,$$
其中
$$U\in {\mathbb{R}}^{m\times r},V\in {\mathbb{R}}^{n\times r}.$$
这样一来，我们把原先可能有 $m\times n$ 个自由参数的矩阵，降低成 $m\times r+n\times r$ 个自由参数。当 $r\ll m,n$ 时，所需参数量将显著降低。

在 推荐系统 中，这样的分解可以用来表示用户与物品之间的潜在交互：

• $U$ 的第 $i$ 行（记作 $U_{i,:}$）可看作用户 $i$ 的“潜在因子”向量；
• $V$ 的第 $j$ 行（记作 $V_{j,:}$）可看作物品（电影、商品等） $j$ 的“潜在因子”向量；
• 用户对物品的评分（或偏好）就近似于二者向量的内积 $(U{V}^T{)}_{ij}$。

在这个思路基础上，还可添加正则化项、偏置项等，形成更实际的 矩阵分解 和 协同过滤 模型。

核范数最小化（Nuclear Norm Minimization）

除了直接做矩阵分解的形式，核范数最小化 在许多低秩场景中也是非常重要且常用的方法。

核范数与最小秩的关系

• 矩阵的核范数（Nuclear Norm）（也称 迹范数 Trace Norm）定义为：
  $$\Vert M{\Vert }_{\ast }=\sum _{i=1}^{\min (m,n)}{\sigma }_i(M),$$
  其中 ${\sigma }_i(M)$ 是矩阵 $M$ 的第 $i$ 个奇异值。

• 矩阵的秩（rank） 可以看作矩阵非零奇异值的个数：
  r a n k ( M ) = # {   i ∣ σ i ( M ) ≠ 0 } . \mathrm{rank}(M) = \#\{\,i \mid \sigma_i(M) \neq 0 \}. rank(M)=#{i∣σi​(M)=0}.

如果我们想让矩阵秩变小，就希望奇异值的个数越少越好。但 最小化 $\mathrm{rank}(M)$ 是一个非凸问题，往往是 NP-hard。作为一种凸松弛做法，我们可以最小化核范数 $\Vert M{\Vert }_{\ast }$ 代替最小化 $\mathrm{rank}(M)$。
因为在几何上，核范数是所有奇异值之和，而秩是非零奇异值的个数。二者的取值趋势是相似的：当一个矩阵的秩较小，其非零奇异值往往集中在前面几个，此时核范数也相对较小。

基于这一思想，人们常常写出下述凸优化形式：
$$\underset{X}{\min }\Vert X{\Vert }_{\ast }\text{subject to }\mathcal{A}(X)=b,$$
其中 $\mathcal{A}$ 表示线性算子（如“采样测量”），$b$ 是观测数据；通过约束 $\mathcal{A}(X)=b$ 逼迫 $X$ 与数据一致，再通过 $\Vert X{\Vert }_{\ast }$ 使 $X$ 保持低秩。

---

矩阵补全问题示例

Netflix问题

Netflix 问题 是协同过滤中的一个经典案例。设：

• $M$ 为用户-物品（例如用户-电影）的评分矩阵，大小为 $m\times n$；
• $\Omega$ 表示观测到评分的位置（即用户对哪些电影给出了评分），$|\Omega |$ 通常远小于 $mn$；
• 目标是根据已有的评分来推断（补全）所有用户对所有物品的评分。

由于用户的兴趣和物品的属性往往受少数几个“潜在因子”主导，人们一般假设 $M$ 是一个 近似低秩矩阵。

最优目标与推导

最朴素的做法可能是：
$$\underset{X}{\min }\mathrm{rank}(X),\text{subject to}{X}_{ij}=M_{ij},\forall (i,j)\in \Omega .$$
即在所有能满足已观测评分的矩阵中找到秩最小者。但这个问题非凸，且往往难以求解。

松弛与等价形式

将秩最小化换成核范数最小化后，就有了核范数最小化矩阵补全：
$$\underset{X}{\min }\Vert X{\Vert }_{\ast }\text{subject to}{X}_{ij}=M_{ij},(i,j)\in \Omega .$$
这是一个凸优化问题，可以利用现有的凸优化算法，如 SVT（奇异值软阈值）、APG（加速近端梯度） 等方法来求解。其数学几何含义是：我们在所有能满足观测值的矩阵中，选取奇异值总和最小者，这往往与选取秩最小者具有相同的效果（在很多情况下等价或近似等价），因此可以极大地减少矩阵的自由度。

---

低秩矩阵求解方法

软阈值奇异值收缩（SVT）

SVT (Singular Value Thresholding) 算法是核范数最小化的一种经典求解思路。核心公式可以写作对奇异值的“软阈值”操作：

• 给定一个矩阵 $Y$，令其 SVD 为
  $$Y=U\Sigma V^T,\Sigma =\mathrm{diag}({\sigma }_1,\dots ,{\sigma }_p),$$
  其中 $p=\min (m,n)$。
• 对对角元素（奇异值）${\sigma }_i$ 做如下变换：
  D τ ( Σ ) = d i a g ( max ⁡ { σ 1 − τ , 0 } , max ⁡ { σ 2 − τ , 0 } , … , max ⁡ { σ p − τ , 0 } ) . D_{\tau}(\Sigma) = \mathrm{diag}(\max\{\sigma_1-\tau,0\}, \max\{\sigma_2-\tau,0\}, \dots, \max\{\sigma_p-\tau,0\}). Dτ​(Σ)=diag(max{σ1​−τ,0},max{σ2​−τ,0},…,max{σp​−τ,0}).
  这一步称为“软阈值（soft-thresholding）”，$\tau$ 是阈值参数。
• 将变换后的奇异值重新与 $U$、$V$ 相乘，
  $${\mathcal{D}}_{\tau }(Y)=U{D}_{\tau }(\Sigma )V^T.$$
• 迭代地使用此操作来逼近最优解。

在矩阵补全问题中，SVT 算法每次会根据已知观测位置对矩阵进行更新，并对更新后的矩阵应用奇异值软阈值收缩，最终在满足约束的同时尽可能降低核范数，从而得到一个近似秩小的矩阵解。

交替最小二乘法（ALS）

如果我们使用 矩阵分解模型 直接去逼近一个部分观测矩阵，可以考虑如下目标：
$$\underset{U,V}{\min }\sum _{(i,j)\in \Omega }(M_{ij}-(U{V}^T{)}_{ij}{)}^2+\lambda (\Vert U{\Vert }_F^2+\Vert V{\Vert }_F^2),$$
其中 $\lambda$ 是正则化系数，以防止过拟合。这个目标函数常见于推荐系统中的矩阵分解算法。为求解它，可以使用 交替最小二乘 (Alternating Least Squares, 简称 ALS)：

1. 固定 $V$，把上式看成关于 $U$ 的二次型，求导并令其为零，即可解出最优 $U$；
2. 固定求得的 $U$，再对 $V$ 做同样操作；
3. 在两个步骤之间来回迭代，直到收敛。

举例来说，固定 $V$ 时，目标函数关于 $U$ 的偏导为：
$$\frac{\partial }{\partial U}(\sum _{(i,j)\in \Omega }(M_{ij}-U_{i,:}{V}_{j,:}^T{)}^2+\lambda \Vert U{\Vert }_F^2)=0,$$
求解可得到一组线性方程。对于每一行 $U_{i,:}$ 的具体更新，也可分块进行。ALS 实现简单，且在大规模数据下只要迭代次数不多，也能达到不错的效果。

梯度方法与凸优化思路

对于 核范数最小化 的问题，除了 SVT，还有以下常用凸优化方法：

• 近端梯度（Proximal Gradient）、加速近端梯度（Accelerated Proximal Gradient, APG）；
• ADMM（交替方向乘子法） 等。

其核心都在于：核范数是奇异值的 ${\ell }_1$ 范数之和，可以在迭代中对矩阵做 奇异值分解 并结合“软阈值”进行近端映射。因为 $\Vert X{\Vert }_{\ast }$ 的近端映射正是上述的 软阈值收缩 操作，这使得核范数最小化在理论上可行并在实践中有较好效率。

---

低秩矩阵应用领域

1. 推荐系统：如 Netflix 问题、电子商务商品推荐，核心思路都是基于用户-物品评分矩阵的低秩假设来预测缺失评分。
2. 图像与视频修复：很多图像在本质上可以用低秩矩阵来描述（或稀疏+低秩组合），对缺损或带噪声的图像进行修复、去背景等都是典型应用。
3. 压缩感知：在高维信号处理中，如果信号或其某种转换矩阵是低秩的，就能用更少的采样去重建完整数据。
4. 协方差矩阵估计：在高维统计和金融分析中，为了避免过拟合和噪声影响，人们常假设协方差矩阵是低秩或接近低秩，从而获得更加鲁棒的估计结果。
5. 自回归模型、时序分析：利用 Hankel 矩阵（包含时序信号）和其潜在的低秩结构来做预测或异常检测。

---

一个简单的Python示例：利用SVD进行低秩近似

下面用一个小的 Python 例子，展示如何使用 截断式 SVD 来得到矩阵的一个秩较低的近似。
假设我们有一个 $6\times 6$ 的随机矩阵 $A$，想把它逼近成秩为 $k$ 的矩阵。

import numpy as np

# 设置随机种子
np.random.seed(42)

# 生成一个 6x6 的随机矩阵
A = np.random.randn(6, 6)
print("原矩阵 A：")
print(A)

# 进行SVD分解
U, S, VT = np.linalg.svd(A, full_matrices=False)

# 设定要保留的秩
rank_k = 2

# 构造只保留前k个奇异值的对角矩阵
S_k = np.zeros_like(S)
S_k[:rank_k] = S[:rank_k]

# 重构低秩近似矩阵 (注意U、VT的大小和S的形状)
A_k = (U * S_k) @ VT

print(f"\n保留前 {rank_k} 个奇异值的低秩近似矩阵 A_k：")
print(A_k)

# 计算Frobenius范数下的逼近误差
error = np.linalg.norm(A - A_k, 'fro')
print(f"\nFrobenius 范数误差: {error:.4f}")

总结

1. 低秩矩阵模型 通过限制矩阵的秩来降低自由度，可以在 矩阵补全、降维、去噪、特征提取 等任务中提供显著优势。
2. SVD 是分析和处理低秩矩阵的关键工具，尤其在 低秩逼近 中有着决定性地位；Eckart–Young–Mirsky 定理为截断式 SVD 在最小二乘意义上的最优性提供了理论支撑。
3. 矩阵分解模型（$M\approx U{V}^T$）和 核范数最小化（凸松弛）是两大主要实现形式：
   • 矩阵分解是直接显式地写出秩为 $r$ 的分解形式；
   • 核范数最小化则是通过最小化 ${\sum }_i{\sigma }_i(M)$ 来隐式地逼近小秩解。
4. 矩阵补全 问题（如 Netflix）将最小秩问题替换为最小核范数问题，利用 SVT 等算法能较好地在缺失数据场景下恢复原矩阵。
5. 求解方法 涉及到 SVT（奇异值软阈值）、ALS（交替最小二乘）、近端梯度法、ADMM 等；根据不同数据规模与需求，选择合适的算法可在效率与收敛精度间取得平衡。
6. 应用范围 已经渗透到推荐系统、图像处理、信号处理、高维统计等等，对理论研究和实际工程都极为关键。