由参数l,r,b,t,n,f定义的透视投影矩阵的推导困惑了我差不多一个多礼拜，这几天几乎是天天都在思考这个问题，昨天晚上3点多钟我突然醒了，然后我又开始想这个问题，结果终于让我给想通了，于是我赶紧起床把这个思路记在了草稿纸上，还专门照了张照片作证。

为了解决这个问题，前几天我专门发了两篇帖子求答案，结果知网上的竟然沉掉了。而在csdn上也没有得到答案（质疑有关透视投影矩阵的推导）。幸亏我自己还是解决了这个问题。
下面推导的是OpenGL中的透视投影矩阵。
已经知道由参数fovy,aspect,n,f定义的透视投影矩阵为：(有关这块的推导可见《3d graphics for game programming》 2.4.3 derivation of projection matrix，讲得非常详细)
POpenGL= <script type="math/tex" id="MathJax-Element-3"> P_{OpenGL} = </script> ⎛⎝⎜⎜⎜⎜⎜⎜⎜cot(fovy2)aspect0000cot(fovy2)0000−f+nf−n−100−2nff−n0⎞⎠⎟⎟⎟⎟⎟⎟⎟ <script type="math/tex" id="MathJax-Element-4"> \begin{pmatrix} \frac{cot(\frac{fovy}{2})}{aspect} & 0 & 0 & 0 \\ 0 & cot(\frac{fovy}{2}) & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} </script> <script type="math/tex" id="MathJax-Element-5"> </script>
那么再看另一种投影参数l,r,b,t,n,f，上面矩阵中：
cot(fovy2)aspect=cot(fovx2)=2nr−l,<script type="math/tex" id="MathJax-Element-6"> \frac{cot(\frac{fovy}{2})}{aspect} = cot(\frac{fovx}{2}) = \frac{2n}{r-l}, </script>
cot(fovy2)=2nt−b. <script type="math/tex" id="MathJax-Element-7"> cot(\frac{fovy}{2}) = \frac{2n}{t-b}. </script>
因为参数l,r是对应视见空间中x轴的坐标，b,t对应视见空间中y轴的坐标，如果l=-r并且b=-t，那么由这种参数定义的透视投影矩阵就是：
P′OpenGL= <script type="math/tex" id="MathJax-Element-8"> P’_{OpenGL} = </script> ⎛⎝⎜⎜⎜⎜⎜2nr−l00002nt−b0000−f+nf−n−100−2nff−n0⎞⎠⎟⎟⎟⎟⎟ <script type="math/tex" id="MathJax-Element-9"> \begin{pmatrix} \frac{2n}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2n}{t-b} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} </script> <script type="math/tex" id="MathJax-Element-10"> </script>
而官方的透视投影矩阵是：
POpenGL=<script type="math/tex" id="MathJax-Element-11"> P_{OpenGL} = </script> ⎛⎝⎜⎜⎜⎜⎜⎜2nr−l00002nt−b00r+lr−lt+bt−b−f+nf−n−100−2nff−n0⎞⎠⎟⎟⎟⎟⎟⎟ <script type="math/tex" id="MathJax-Element-12"> \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} </script> <script type="math/tex" id="MathJax-Element-13"> </script>
实际上这个矩阵是由两步转换完成的，第一步是进行矩阵P′OpenGL<script type="math/tex" id="MathJax-Element-14">P'_{OpenGL}</script>变换，然后进行了平移操作，如下：

POpenGL=T×P′OpenGL=⎛⎝⎜⎜⎜⎜⎜⎜⎜100001000010−r+lr−l−t+bt−b01⎞⎠⎟⎟⎟⎟⎟⎟⎟×⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜2nr−l00002nt−b0000−f+nf−n−100−2nff−n0⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜2nr−l00002nt−b00r+lr−lt+bt−b−f+nf−n−100−2nff−n0⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟

<script type="math/tex; mode=display" id="MathJax-Element-15">\begin{align} P_{OpenGL} & = T×P'_{OpenGL} \\ & = \begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & 1 & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} × \begin{pmatrix} \frac{2n}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2n}{t-b} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} \\ & = \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} \end{align}</script>
那些说这个透视投影没有做平移这一步操作，我可以100%跟你说你是错的！
下面我来解释为什么进行了平移操作。
来张示意图：

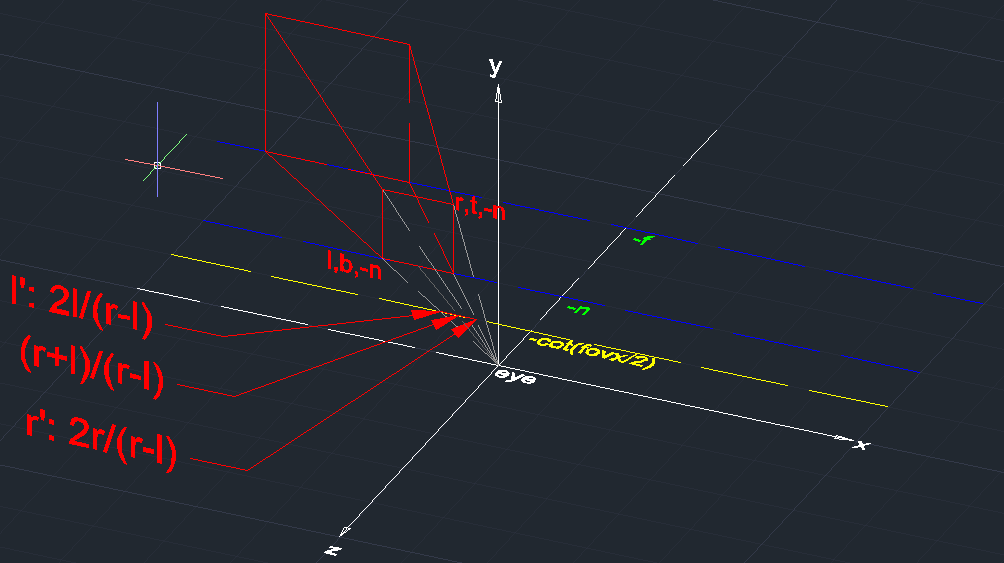
这个是视见空间中的示意图，因为存在l≠-r或b≠-t的情况，所以这里我故意没把近裁剪平面中心画在z轴上。 示意图上由红线绘制的立方体才是由l,r,b,t,n,f参数定义的视锥体，其中远裁剪平面上的四个点分别对应原点eye经过近裁剪平面上四个点的延长线与z=-f平面的交点，注意这个视锥体是不规则的！然后图中的标注l’, r’是近裁剪平面点(l,b,-n)和点(r,b,-n)x轴上的分量在 z=−cot(fovx2) <script type="math/tex" id="MathJax-Element-16">z=-cot(\frac{fovx}{2})</script>上的投影， l′=2lr−l <script type="math/tex" id="MathJax-Element-17">l'=\frac{2l}{r-l}</script>， r′=2rr−l <script type="math/tex" id="MathJax-Element-18">r'=\frac{2r}{r-l}</script>，l’和r’的中心值是 r+lr−l <script type="math/tex" id="MathJax-Element-19">\frac{r+l}{r-l}</script>，同理近裁剪平面上点(r,b,-n)和点(r,t,-n)y轴上的分量在 z=−cot(fovy2) <script type="math/tex" id="MathJax-Element-20">z=-cot(\frac{fovy}{2})</script>上的投影， b′=2bt−b <script type="math/tex" id="MathJax-Element-21">b'=\frac{2b}{t-b}</script>， t′=2tt−b <script type="math/tex" id="MathJax-Element-22">t'=\frac{2t}{t-b}</script>，b’和t’的中心值是 t+bt−b <script type="math/tex" id="MathJax-Element-23">\frac{t+b}{t-b}</script>。 图中的视锥体通过 P′OpenGL <script type="math/tex" id="MathJax-Element-24">P'_{OpenGL}</script>透视变换之后得到的是规则的正方体（左下角顶点 (2lr−l,2bt−b,1) <script type="math/tex" id="MathJax-Element-25">(\frac{2l}{r-l},\frac{2b}{t-b},1)</script>，右上角顶点 (2rr−l,2tt−b,−1)） <script type="math/tex" id="MathJax-Element-26">(\frac{2r}{r-l},\frac{2t}{t-b},-1)）</script>，最终要把它转换成cvv（canonical view volume，正规可视化空间），则需要进行T平移转换，也就是平移 (−r+lr−l,−t+bt−b,0) <script type="math/tex" id="MathJax-Element-27">(-\frac{r+l}{r-l}, -\frac{t+b}{t-b}, 0)</script>。得证。