一 问题描述

1.前面也写了一篇相关的svd分解求旋转平移的，但是权重是全当为1来算的，重新遇到后带权重的svd计算旋转平移后就不会了，也理解不够透，特此重新记录一下。
2.一般情况下这个加权版本的svd求解会和GNC结合求解，下一篇文章会写与GNC结合(待更新)

假设$P=p_1,p_2,...,p_n$和$Q=q_1,q_2,...,q_n$是两组$R^d$空间中的对应点集，现在想要根据这个两个点集的数据来计算出它们之间的刚性转置信息，可以知道这其实是一个最小二乘求优问题，问题可以用如下计算式描述：

其中$w_i>0$，是点集中每个点对的权重。

要求(1)式中的最小值，即为求式中对R和t求导数为0的解。

二 计算位移

将(1)式中的$R$设为不变量对$t$进行求导，同时令$F(t)=(R,t)$，对$F(t)$求导可得：

从上可以看出，问题经过转化后变得更加简单，对原来的点集做一个减中心点的预处理，然后再求两个最小二乘的旋转量。

三 计算旋转量

将(8)式用矩阵表示形式展开，可得：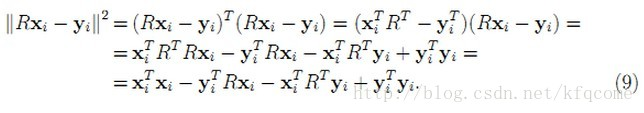

（由于旋转矩阵$R$是正交矩阵，因而有$R{R}^T=I$）。同时可以知道上式中$y_i^{T}R{x}_i$和$x_i^T{R}^T{y}_i$都是标量，而一个标量的转置仍然等于标量本身，因而有：

现在变成要求(11)式的最小值，而该式中只有一项与$R$有关，其他两项($x_{i}T{x}_i$和$y_{i}T{y}_i$)都是常量，所以问题转换为求其中一项可变量的最小值，即

(14)式中的转换是将累加转换成矩阵相乘，其中$W$是$n\times n$的对角矩阵，$X$和$Y$是$3\times n$的矩阵，这些矩阵相乘后的迹就等于等式左边的值。同时，对于矩阵的迹，有如下变换关系：

(18)式中最后一步的变换也用到了(15)式的性质。由于$U、R、V$都是正交矩阵，那么$M=V^{T}RU$也是正交矩阵。

由上述两式可以知道，要求最大迹，就必须使得$m_{ii}$的值等于1，而$M$又是正交矩阵，那么$M$就必然是单位矩阵，即有
$M=I=V^{T}RU=>V=RU=>R=V{U}^T(21)$

四 旋转结果校正

到上面(21)式为止，求得的$R$是最优的正交矩阵，但是这个正交矩阵既可以是旋转矩阵，也可以是反射矩阵。反射矩阵参见博文“旋转和反射”。
根据R的行列式值可以判断该结果是旋转矩阵还是反射矩阵，假如是反射矩阵，那么其行列式值就为-1。如果我们严格限定我们求解的必须是旋转矩阵，那么当前求解出来的反射矩阵就不符合要求。这个时候就必须求解下一个符合要求的最优解。
将目标问题重新组织成如下形式：

如果我们将$m_{ii}$当作变量，它的取值范围就是[-1,1]。函数$f$对于$m_{ii}$来说是线性的，所以它在定义域的边界上才取得极值。很显然对于所有的mii来说，所有都取1能取得最大的极值，但是该取值必须被排除（用这个得出的$R$是反射矩阵），那么下一个最优的($m_{11},m_{22},...,m_{dd}$)取值就是(1,1,…1,-1)，即除最后一个值取-1外，其他的值仍然为1。

为什么是取最后一个mdd为-1，这是进行SVD分解之后，Σ矩阵里对角线上的值经过了排序的，即σd的值最小。

example(实例计算，整个计算流程：)

假设$p$和$q$是两组$R^d$空间中的对应点集。输入时，$p$和$q$为3×n的矩阵

1.计算加权质心

代码

p_w = w(1:size(p,2))'.*p;
q_w = w(1:size(q,2))'.*q;
p_center=mean(p_w,2)/mean(w);%求p每一行的平均数，得到一个3×1得矩阵,即得质心(注意此时已经Uy已经转置，列表示一个点的xyz坐标)
q_center=mean(q_w,2)/mean(w);

2.去重心

代码

p_c=p-p_center*ones(1,size(p,2));%3*1 * 1*8 = 3*8 这是把之质心坐标复制成了8份,方便原数组里面得值与质心相减
q_c=q-q_center*ones(1,size(q,2));

3.构建S(前面我的一篇文章写的H)矩阵，并进行svd分解

H=zeros(3,3);
%构建H矩阵，并SVD分解
for j=1:size(p_c,2)%取列数的大小遍历
    H=H+w(j)*p_c(:,j)*q_c(:,j)';
end
[U,~,V]=svd(H);

4.计算旋转平移

代码

Rf=V*U';%两点云之间的旋转矩阵                                             
% fprintf('旋转矩阵验证(等于1表明svd求解R有效,若为-1则无效)= %g\n',det(Rf))%等于1表明R有效。若为-1则无效
Tf=p_center-Rf*q_center;  


T_t=[Rf,Tf];
T_t=[T_t;0,0,0,1];
T_t = inv(T_t);%数据集的制作，是由点云P乘以T得到的Q，这里用SVD求解的得到的T_t是T的逆，所以需要inv(T_t)变到和T成同一个方向的变换矩阵才能更好的去算误差（或者把inv(T)变到与T_t成同一个方向也行）。

总代码

1.假设$p$和$q$是两组$R^d$空间中的对应点集。输入时，$p$和$q$为3×n的矩阵
2.这里权重全设为1了，一般情况下这个加权版本的svd求解会和GNC结合求解，下一篇文章会写与GNC结合(待更新)

function T_t = svd_solution(p,q)
	w = [1:size(p,2)];
    p_w = w'.*p;
    q_w = w'.*q;
    
    p_center=sum(p_w,2)/sum(w);%求p每一行的平均数，得到一个3×1得矩阵,即得质心(注意此时已经Uy已经转置，列表示一个点的xyz坐标)
    q_center=sum(q_w,2)/sum(w);
    %与上面效果一样
    %p_center=mean(p_w,2)/mean(w);%求p每一行的平均数，得到一个3×1得矩阵,即得质心(注意此时已经Uy已经转置，列表示一个点的xyz坐标)
    %q_center=mean(q_w,2)/mean(w);
    
    %去重心
    p_c=p-p_center*ones(1,size(p,2));%3*1 * 1*8 = 3*8 这是把之质心坐标复制成了8份,方便原数组里面得值与质心相减
    q_c=q-q_center*ones(1,size(q,2));
    
    
    
    H=zeros(3,3);
    %构建H矩阵，并SVD分解
    for j=1:size(p_c,2)%取列数的大小遍历
        H=H+w(j)*p_c(:,j)*q_c(:,j)';
    end
    [U,~,V]=svd(H);
    Rf=V*U';%两点云之间的旋转矩阵                                             
    % fprintf('旋转矩阵验证(等于1表明svd求解R有效,若为-1则无效)= %g\n',det(Rf))%等于1表明R有效。若为-1则无效
    
    Tf=p_center-Rf*q_center;
    
    
    T_t=[Rf,Tf];
    T_t=[T_t;0,0,0,1];
    T_t = inv(T_t);%数据集的制作，是由点云P乘以T得到的Q，这里用SVD求解的得到的T_t是T的逆，所以需要inv(T_t)变到和T成同一个方向的变换矩阵才能更好的去算误差（或者把inv(T)变到与T_t成同一个方向也行）。
end

参考文献：http://igl.ethz.ch/projects/ARAP/svd_rot.pdf