<script type="math/tex; mode=display" id="MathJax-Element-5"> \nabla_Af(A) = \begin{bmatrix} \frac{\partial f}{\partial A_{11}} & \cdots & \frac{\partial f}{\partial A_{1n}} \\ \vdots & \ddots & \vdots\\ \frac{\partial f}{\partial A_{m1}} & \cdots & \frac{\partial f}{\partial A_{mn}} \\ \end{bmatrix} </script>
举个例子,如果 A=[A11A21A12A22] <script type="math/tex" id="MathJax-Element-6">A = \begin{bmatrix}A_{11} & A_{12} \\ A_{21} & A_{22}\end{bmatrix}</script>是一个2*2的矩阵,函数 f <script type="math/tex" id="MathJax-Element-7">f</script>定义如下:
f(A)=32A11+5A212+A21A22.
<script type="math/tex; mode=display" id="MathJax-Element-8"> f(A) = \frac{3}{2}A_{11} + 5A_{12}^2 + A_{21}A_{22}. </script>
根据矩阵偏导公式可求得:
∇Af(A)=⎡⎣32A2210A12A21⎤⎦
<script type="math/tex; mode=display" id="MathJax-Element-9"> \nabla_Af(A) = \begin{bmatrix} \frac{3}{2} & 10A_{12} \\ A_{22} & A_{21}\\ \end{bmatrix} </script>
我们引入矩阵的迹,写作“ tr <script type="math/tex" id="MathJax-Element-10">\mathrm{tr}</script>”。对于一个n阶方阵A,它的迹是其对角线元素之和:
trA=∑i=1nAii
<script type="math/tex; mode=display" id="MathJax-Element-11"> \mathrm{tr}A = \sum_{i=1}^n A_{ii} </script>
如果a是一个实数(也可看成1-by-1矩阵),有 tra=a <script type="math/tex" id="MathJax-Element-12">\mathrm{tr}a = a</script>。迹操作符有这样的性质:如果矩阵 A <script type="math/tex" id="MathJax-Element-13">A</script>和B<script type="math/tex" id="MathJax-Element-14">B</script>满足 AB <script type="math/tex" id="MathJax-Element-15">AB</script>是方阵,则有 trAB=trBA <script type="math/tex" id="MathJax-Element-16">\mathrm{tr}AB = \mathrm{tr}BA</script>,由此可推得:
trABC=trCAB=trBCAtrABCD=trDABC=trCDAB=trBCDA
<script type="math/tex; mode=display" id="MathJax-Element-17"> \begin{align} \mathrm{tr}ABC = \mathrm{tr}CAB = \mathrm{tr}BCA\qquad\qquad\\ \mathrm{tr}ABCD = \mathrm{tr}DABC = \mathrm{tr}CDAB = \mathrm{tr}BCDA\\ \end{align} </script>
迹操作符的下列性质也容易证明。其中 A <script type="math/tex" id="MathJax-Element-18">A</script>和B<script type="math/tex" id="MathJax-Element-19">B</script>是方阵, a <script type="math/tex" id="MathJax-Element-20">a</script>是实数:
trAtr(A+B)traA=trAT=trA+trB=atrA
<script type="math/tex; mode=display" id="MathJax-Element-21"> \begin{align} \mathrm{tr}A &= \mathrm{tr}A^T\\ \mathrm{tr} (A + B) &= \mathrm{tr}A + \mathrm{tr}B\\ \mathrm{tr} aA &= a\mathrm{tr}A\\ \end{align} </script>
结合矩阵的迹和矩阵导数,可以给出下列公式:
∇AtrAB∇ATf(A)∇AtrABATC∇A|A|=BT=(∇Af(A))T=CAB+CTABT=|A|(A−1)T(1)(2)(3)(4)
<script type="math/tex; mode=display" id="MathJax-Element-22"> \begin{align} \nabla_A \mathrm{tr}AB &= B^T &(1)\\ \nabla_{A^T} f(A) &= (\nabla_{A} f(A))^T &(2)\\ \nabla_A \mathrm{tr}ABA^TC &= CAB + C^TAB^T \qquad \qquad &(3)\\ \nabla_A |A| &= |A|(A^{-1})^T &(4)\\ \end{align} </script>
其中(4)只在矩阵A为满秩矩阵时成立。
2.2 二顾最小方差
了解了矩阵导数这一工具后,为了实现最小化 J(θ) <script type="math/tex" id="MathJax-Element-23">J(\theta)</script>的目标,我们先设法将成本函数 J <script type="math/tex" id="MathJax-Element-24">J</script>用向量表示。
给定一个训练集,我们将其以m-by-n矩阵X<script type="math/tex" id="MathJax-Element-25">X</script>的形式表示,其中每一行代表一个训练样本:
X=⎡⎣⎢⎢⎢⎢⎢−(x(1))T−−(x(2))T−⋮−(x(m))T−⎤⎦⎥⎥⎥⎥⎥
<script type="math/tex; mode=display" id="MathJax-Element-26"> X = \begin{bmatrix} -(x^{(1)})^T-\\ -(x^{(2)})^T-\\ \vdots\\ -(x^{(m)})^T-\\ \end{bmatrix} </script>
同时将包含所有目标值的 y⃗ <script type="math/tex" id="MathJax-Element-27">\vec{y}</script>表示为一个m维的列向量:
y⃗ =⎡⎣⎢⎢⎢⎢⎢y(1)y(2)⋮y(m)⎤⎦⎥⎥⎥⎥⎥
<script type="math/tex; mode=display" id="MathJax-Element-28"> \vec{y} = \begin{bmatrix} y^{(1)}\\ y^{(2)}\\ \vdots\\ y^{(m)}\\ \end{bmatrix} </script>
因为 hθ(x(i))=(x(i))Tθ <script type="math/tex" id="MathJax-Element-29">h_\theta(x^{(i)}) = (x^{(i)})^T \theta</script>,我们可以很容易地证明:
Xθ−y⃗ =⎡⎣⎢⎢⎢(x(1))Tθ⋮(x(m))Tθ⎤⎦⎥⎥⎥−⎡⎣⎢⎢y(1)⋮y(m)⎤⎦⎥⎥=⎡⎣⎢⎢hθ(x(1))−y(1)⋮hθ(x(m))−y(m)⎤⎦⎥⎥
<script type="math/tex; mode=display" id="MathJax-Element-30"> \begin{align} X\theta - \vec{y} &= \begin{bmatrix} (x^{(1)})^T\theta \\ \vdots \\ (x^{(m)})^T \theta \\ \end{bmatrix} - \begin{bmatrix} y^{(1)}\\ \vdots\\ y^{(m)}\\ \end{bmatrix}\\ &= \begin{bmatrix} h_\theta (x^{(1)}) - y^{(1)}\\ \vdots\\ h_\theta (x^{(m)}) - y^{(m)}\\ \end{bmatrix}\\ \end{align} </script>
对于一个向量 z <script type="math/tex" id="MathJax-Element-31">z</script>,有zTz=∑iz2i<script type="math/tex" id="MathJax-Element-32">z^Tz = \sum_i z_i^2</script>,则:
12(Xθ−y⃗ )T(Xθ−y⃗ )=12∑i=1m(hθ(x(i))−y(i))2=J(θ)
<script type="math/tex; mode=display" id="MathJax-Element-33"> \begin{align} \frac{1}{2} (X\theta - \vec{y})^T (X\theta - \vec{y}) &= \frac{1}{2} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 \\ &= J(\theta) \end{align} </script>
最后要最小化 J <script type="math/tex" id="MathJax-Element-34">J</script>,我们要求解它关于θ<script type="math/tex" id="MathJax-Element-35">\theta</script>的导数:
∇θJ(θ)=∇θ12(Xθ−y⃗ )T(Xθ−y⃗ )=12∇θ(θTXTXθ−θTXTy⃗ −y⃗ TXθ+y⃗ Ty⃗ )=12∇θtr(θTXTXθ−θTXTy⃗ −y⃗ TXθ+y⃗ Ty⃗ )=12∇θ(trθTXTXθ−2try⃗ TXθ)=12(XTXθ+XTXθ−2XTy⃗ )=XTXθ−XTy⃗
<script type="math/tex; mode=display" id="MathJax-Element-36"> \begin{align} \nabla_\theta J(\theta) &= \nabla_\theta \frac{1}{2} (X\theta - \vec{y})^T (X\theta - \vec{y})\\ &= \frac{1}{2} \nabla_\theta (\theta^T X^T X \theta - \theta^T X^T \vec{y} - \vec{y}^T X \theta + \vec{y}^T\vec{y})\\ &= \frac{1}{2} \nabla_\theta \mathrm{tr} (\theta^T X^T X \theta - \theta^T X^T \vec{y} - \vec{y}^T X \theta + \vec{y}^T\vec{y})\\ &= \frac{1}{2} \nabla_\theta (\mathrm{tr} \theta^T X^T X \theta - 2 \mathrm{tr} \vec{y}^T X \theta)\\ &= \frac{1}{2} (X^T X \theta + X^T X \theta - 2 X^T \vec{y})\\ &= X^T X \theta - X^T \vec{y}\\ \end{align} </script>
为了最小化 J(θ) <script type="math/tex" id="MathJax-Element-37">J(\theta)</script>,我们要设法使其偏导数为零,这样就可推出正规方程:
XTXθ=XTy⃗
<script type="math/tex; mode=display" id="MathJax-Element-38"> X^T X \theta = X^T \vec{y} </script>
那么权重矩阵 θ <script type="math/tex" id="MathJax-Element-39">\theta</script>,应该调整为:
θ=(XTX)−1XTy⃗
<script type="math/tex; mode=display" id="MathJax-Element-40"> \theta = (X^T X)^{-1} X^T \vec{y} </script>
举个例子,硝酸钠的溶解度试验中,测得不同温度x(单位:C)下,硝酸钠溶解于水中的溶解度y%的数据如下:
| 温度 |
0 |
4 |
10 |
15 |
21 |
29 |
36 |
51 |
68 |
| 溶解度(%) |
66.7 |
71.0 |
76.3 |
80.6 |
85.7 |
92.9 |
99.4 |
113.6 |
125.1 |
求 y <script type="math/tex" id="MathJax-Element-41">y</script>和x<script type="math/tex" id="MathJax-Element-42">x</script>的经验回归函数。
从上面的数据中可以,写出输入特征矩阵 X <script type="math/tex" id="MathJax-Element-43">X</script>和目标变量矩阵y⃗ <script type="math/tex" id="MathJax-Element-44">\vec{y}</script>。
Xy⃗ =[1014110115121129136151168]T=[66.771.076.380.685.792.999.4113.6125.1]T
<script type="math/tex; mode=display" id="MathJax-Element-45"> \begin{align} X &=\left[ \begin{matrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 0 & 4 & 10 & 15 & 21 & 29 & 36 & 51 & 68\\ \end{matrix} \right]^T \\ \vec{y} &= [ \begin{matrix} 66.7 & 71.0 & 76.3 & 80.6 & 85.7 & 92.9 & 99.4 & 113.6 & 125.1 \end{matrix} ]^T \\ \end{align} </script>
代入公式 θ=(XTX)−1XTy⃗ <script type="math/tex" id="MathJax-Element-46">\theta = (X^T X)^{-1} X^T \vec{y}</script>中求解权重 θ <script type="math/tex" id="MathJax-Element-47">\theta</script>的值,得:
θ0=67.5078,θ1=0.8706
<script type="math/tex; mode=display" id="MathJax-Element-48"> \theta_0 = 67.5078, \qquad \theta_1 = 0.8706 </script>
于是所求的线性回归假设为:
y=67.5078+0.8706x.
<script type="math/tex; mode=display" id="MathJax-Element-49"> y = 67.5078 + 0.8706x. </script>
下图将训练样本和回归函数绘制在一起:
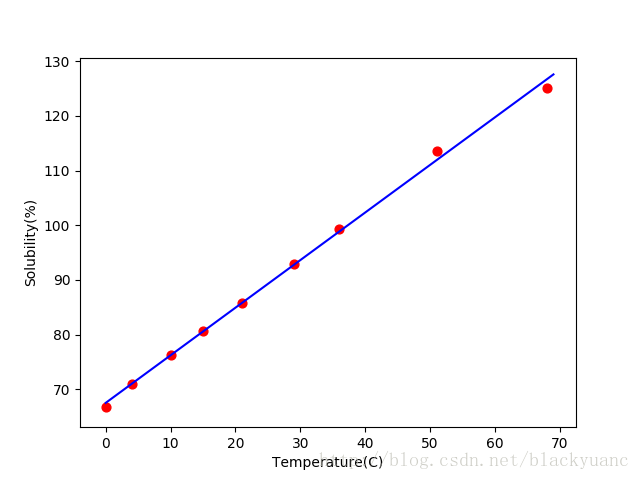
实现的python代码如下:
import matplotlib.pyplot as plt
import numpy as np
X = np.array([0 , 4, 10, 15, 21, 29, 36, 51, 68])
y = np.array([[66.7, 71.0, 76.3, 80.6, 85.7, 92.9, 99.4, 113.6, 125.1]])
X_0 = np.ones(len(X)).astype(dtype=np.int)
X_new = np.array([X_0, X])
temp = np.matrix(np.dot(X_new, X_new.T))
ans_matrix = temp ** -1 * X_new * y.T
intercept = np.array(ans_matrix)[0][0]
coef = np.array(ans_matrix)[1][0]
lx = np.arange(0, 70)
ly = coef * lx + intercept
plt.plot(lx, ly, color='blue')
plt.scatter(X, y, c='red', s=40, marker='o')
plt.xlabel('Temperature(C)')
plt.ylabel('Solubility(%)')
plt.show()
在特征维度少的情况下,正规方程组的计算会比梯度下降法快很多,推荐计算线性回归时多使用该方法。
 已为社区贡献4条内容
已为社区贡献4条内容








所有评论(0)