波束形成基于空域谱估计重建协方差矩阵的稳健自适应波束形成算法

文献 Covariance Matrix Reconstruction Based on Power Spectral Estimation and Uncertainty Region for Robust Adaptive Beamforming-TAES-2022

量大龙神魔

1132人浏览 · 2023-06-02 18:40:29

量大龙神魔 · 2023-06-02 18:40:29 发布

前言

这篇文章是基于2012年的TSP的一篇线积分重建协方差矩阵的工作，提出的一种加权线积分重构协方差阵的方法，关于12年的那片线积分协方差重建法可参考YHCANDOU大佬的博客。看完这篇文章个人感觉其中有部分编辑错误，同时在此简单记录。

这篇文章基于的是传统的积分思想，因此整篇文章作者分成了期望导向矢量估计、干扰加噪声角度不确定域估计、干扰加噪声协方差矩阵重建三部分。

期望导向矢量估计

根据子空间正交理论，及信号协方差阵的结构，可得信号的导向矢量可由信号子空间线性表出，则进一步可得信号子空间中的导向矢量与噪声子空间中的导向矢量是正交的，有：

$\mathbf{A}^H\mathbf{U}_n=\mathbf{0}$

则：

$\begin{aligned}\hat{\theta}_k=\underset{\hat{\theta}}{\text{argmin}}\|\mathbf{a}^H(\hat{\theta})\mathbf{U}_n\|_\text{F}^2,&k=1,\cdots,K\end{aligned}$

显然，这部分作者少加了个约束，没了这个约束在多个信源的情况下就会有多个极值点，这一部分约束通常表示为在先验信号方向的周围设置一不确定域以精确寻找局部极值点。作者根据得到的角度得到期望导向矢量。

由于自适应波束形成算法的阵列结构特点，阵列可看作一MA过程或一FIR滤波器，即具有着平坦的谱峰、较大的主瓣以及尖锐的零陷，因此干扰零陷失配对信噪比增益的影响比期望信号失配带来的影响大得多。基于此，作者提出了一种考虑干扰持续移动的情景，并构造了一等式以对其近似：

$\theta_k(t_n)=\hat{\theta}_k+\frac{\Delta\theta_k(t_n)}{N}(t_n-\frac{N}{2}),\quad n=1,\cdots,N$

其中 $N$ 为总快拍数， $\Delta\theta_k(t_n)$ 为角度不确定区域的变化。(这里有一点有问题的是， $t_n = N/2$ 时刻，该等式显然在期干扰信号方向轻微扰动下是不成立的)

等号左边的为时刻估计得到的角度 $\theta_k(t_n)$ ，由以下等式获得：

$\theta_k(t_n)=\underset{\theta\in\Theta_x}{\text{argmax}}|\mathbf{x}^H(t_n)\mathbf{a}(\theta)|,\quad n=1,\cdots,N$

其中 $\Theta_\text{x}=[\hat{\theta}_k-c,\hat{\theta}_k+c]$ 为一小角度域。

(这里有一点有问题的是，该等式可以想成是单快拍期望信号与导向矢量的一个互相关，在理想情况下该式求得的极值点即为真实信号来向，但是本人在仿真过程中发现，噪声的影响下单快拍携带的信息难免会产生不小的失真，虽然该算法只是为角度区域的划分提供依据。)

因此有：

$\theta_k(t_n)=\underset{\theta\in\Theta_x}{\text{argmax}}|\mathbf{x}^H(t_n)\mathbf{a}(\theta)| = \hat{\theta}_k+\frac{\Delta\theta_k(t_n)}{N}(t_n-\frac{N}{2})\\\Rightarrow \Delta\theta_k(t_n)=\big(\frac{2N}{2t_n-N}\big)\big(\underset{\theta\in\Theta_x}{\text{argmax}}|\mathbf{x}^H(t_n)\mathbf{a}(\theta)|-\hat{\theta}_k\big)$

噪声、干扰与期望信号功率估计

作者根据估计得到的角度，构建对应的名义导向矢量。

已知接收信号可表示为：

$\mathbf{x}(t)=\mathbf{a}_1s_1(t)+\sum\limits_{k=2}^K\mathbf{a}_k s_k(t)+\mathbf{n}(t)$

其中：

$\mathbf{a}_i = \mathbf{a}\left ( \hat {\theta}_i \right )$

则对接收信号进一步左乘名义导向矢量共轭转置，有：

$z_k(t)=\textbf{a}_k^H\textbf{x}(t)=\textbf{a}_k^H\textbf{a}_1s_1(t)+~\textbf{a}_k^H\Big(\sum\limits_{k=2}^K\textbf{a}_k s_k(t)+~\textbf{n}(t)\Big)\approx~ \mathbf{a}_k^H\mathbf{a}_k s_k(t)+~\mathbf{a}_k^H\mathbf{n}(t)$

(两个欧氏距离较大的导向矢量其相关很低，MUSIC算法从某一角度可以这么解释。)

其自相关函数为：

$\hat{r}_{z_k}=\frac{1}{N}\sum_{n=1}^N|z_k(t_n)|^2=\hat{\sigma}_k^2\mathbf{a}_k^H\mathbf{a}_k\mathbf{a}_k^H\mathbf{a}_k+\hat{\sigma}_n^2\mathbf{a}_k^H\mathbf{a}_k=\hat{\sigma}_k^2M^2+\hat{\sigma}_n^2M$

即得第 $k$ 个源的功率为：

$\hat{\sigma}_k^2=\frac{\hat{r}_{z_k}-\hat{\sigma}_n^2M}{M^2}$

对于噪声的功率，作者采用的是接收信号自相关阵的噪声子空间对应的特征向量求平均。

干扰加噪声协方差矩阵重建

这部分作者的主要思想便是对干扰加噪声协方差阵进行加权线积分，如下所示：

$\begin{aligned}\hat{\mathbf{R}}_{\text{in}}=\hat{\gamma}_{\text{L}}\int_{-\pi}^{\pi}\mathbf{a}(\theta)\mathbf{a}^{H}(\theta)d\theta +(\hat{\gamma}_{\text{H}}-\hat{\gamma}_{\text{L}})\int_{-\pi}^{\pi}I_{\Theta_{k}}(\theta)\mathbf{a}(\theta)\mathbf{a}^{H}(\theta)d\theta\end{aligned},\hat{\gamma}_{\text{H}}\gg ~\hat{\gamma}_{\text{L}}$

$I_{\Theta_k}(\theta_k)=\begin{cases}1,&\theta_k\in\Theta_k\\ 0,&\text{Otherwise}\end{cases}$

其中 $I_{\Theta_k}(\theta_k)$ 为一门限函数。该式分为两部分，第一部分是对整个角度域进行积分，第二个部分是对干扰域进行加权积分。其简化形式为：

$\begin{aligned}\hat{\mathbf{R}}_{\text{in}}=2\pi\hat{\gamma}_{\text{L}}\mathbf{I}+(\hat{\gamma}_{\text{H}}-\hat{\gamma}_{\text{L}})\sum_{i=1}^{Q_{\text{in}}}\mathbf{a}(\theta_{n_{i}})\mathbf{a}^H(\theta_{n_{i}})\Delta\theta\end{aligned}\\~~~~~~=2\pi\hat{\gamma}_\text{L}\mathbf{I}+(\hat{\gamma}_\text{H}-\hat{\gamma}_\text{L})\mathbf{R}_\text{in}^r=2\pi\hat{\gamma}_\text{L}(\mathbf{I}+\frac{\hat{\gamma}_\text{H}-\hat{\gamma}_\text{L}}{2\pi\hat{\gamma}_\text{L}}\mathbf{R}_\text{in}^r)$

其中 $\mathbf{R}_\text{in}^r$ 为干扰角度域上的协方差阵积分，有 $\mathbf{R}_{\mathrm{in}}^r =\sum_{i=1}^{Q_\text{in}}\mathbf{a}(\theta_{n_i})\mathbf{a}^H(\theta_{n_i})\Delta\theta$ 。

对于协方差矩阵权重系数求解，其中的噪声域部分权重为：

$\hat{\gamma}_L= \frac{1}{2\pi}\hat{\sigma}_n^2$

而信号域部分权重为：

$\hat{\gamma}_H=\max\{\hat{\sigma}_k^2\}_{k=2}^K+\hat{\gamma}_L$

(这一部分个人感觉有点勉强，虽然其主要思想是通过对波束图重新构建，重构干扰加噪声协方差阵，相当于变相求解在高信噪比情况下的权向量。此外从这可看出，决定波束形成器零陷深度的从求得的各信源功率变成了统一化的 $\hat{\gamma}_H$ )

最后所求解的权向量为：

$\mathbf{w}_{\text{PSEUR}}=\frac{\hat{\mathbf{R}}_{\text{in}}^{-1}\mathbf{a}(\hat{\theta}_1)}{\mathbf{a}(\hat{\theta}_1)^{\text{H}}\hat{\mathbf{R}}_{\text{in}}^{-1}\mathbf{a}(\hat{\theta}_1)}$

仿真

部分仿真条件如表所示：

阵元数	10
信噪比	0
扰噪比	20
阵元间距	半波长
信源数	1
干扰数	2
信源到达角	5°
干扰到达角	-30°，45°
信源角度估计误差	[0°,3°]
角度采样步长	0.1°
随机采样点数L	10
角度搜索范围 $c$	4°

代码如下所示：

clc;
clear;
jk = 0;
loop = 50;
SINRO = zeros(1,length(-20:5:40));
snr = 0;
deg_dev_predf = 3;%%预定义的角度最大偏移量
ang_mismatch1 = randi(deg_dev_predf*2)-deg_dev_predf;
ang_mismatch2 = randi(deg_dev_predf*2)-deg_dev_predf;
ang_mismatch3 = randi(deg_dev_predf*2)-deg_dev_predf; %%三个不同方向的DOA误差
%% 初始化及设定参数
array_num = 10;%%阵元数
snapshot_num = 30;%%快拍数
source_aoa = [5,-30,45];%%信源到达角
tgt_ang = 1;
c = 340;%%波速
f = 1000;%%频率
lambda = c/f;%%波长
d = 0.5*lambda;
inr1 = 20;
inr2 = 20;
source_num = length(source_aoa);%%信源数
sig_nr = [snr,inr1,inr2];%%信号功率dBw
deg_deviate = 3;%%误差角度偏离
source_dev = source_aoa+[ang_mismatch1,ang_mismatch2,ang_mismatch3];
reco_size = 8;
reso = 0.1;

%% 转向矢量
a_bar = exp(-1i*(0:array_num-1)'*pi*sind((source_dev(tgt_ang))));%%实际带有误差的阵列响应矢量
A = exp(-1i*(0:array_num-1)'*2*pi*(d/lambda)*sind(source_aoa));%%阵列响应矩阵
tar_sig = wgn(1,snapshot_num,sig_nr(tgt_ang));
inf1 = wgn(1,snapshot_num,sig_nr(2));
inf2 = wgn(1,snapshot_num,sig_nr(2));
n = (randn(array_num,snapshot_num)+randn(array_num,snapshot_num)*1i)/sqrt(2);
rec_sig = A(:,1)*tar_sig+A(:,2)*inf1+A(:,3)*inf2+n;
R = rec_sig*rec_sig'/snapshot_num;%%接收阵的协方差矩阵
[U,Gamma,V] = svd(R);
Rs = A(:,1)*tar_sig*(A(:,1)*tar_sig)'/snapshot_num;
Ri = (A(:,2)*inf1+A(:,3)*inf2)*(A(:,2)*inf1+A(:,3)*inf2)'/snapshot_num;
Rn = n*n'/snapshot_num;
Us = U(:,1:source_num);
Un = U(:,source_num+1:end);
%% 算法
pow_n = sum(diag(Gamma(source_num+1:end,source_num+1:end)))/(array_num-source_num);
Gamma_lb = pow_n/(2*pi);
for ik = 1:source_num
    ang_est(ik) = get_max_theta(Un,source_dev(ik),reco_size,reso);
    A_est(:,ik) = exp(-1i*(0:array_num-1)'*pi*sind(ang_est(ik)));
    for lk = 1:snapshot_num
        delta_theta_k(ik,lk) = (2*snapshot_num/(2*lk-snapshot_num))*(get_max_theta(rec_sig(:,lk),ang_est(ik),reco_size/2,reso)-ang_est(ik));
    end
    zk = A_est(:,ik)'*(rec_sig);
    rzk = sum(abs(zk).^2/snapshot_num);
    pow_k(ik) = rzk/array_num^2-pow_n/array_num;
end
R_i_n = pow_n*eye(array_num);
for ik = 2:source_num
    R_i_n = R_i_n+pow_k(ik)*A_est(:,ik)*A_est(:,ik)';
end
w0 = inv(R_i_n)*A_est(:,1)/(A_est(:,1)'*inv(R_i_n)*A_est(:,1));
beam_plot(w0);

function theta = get_max_theta(xt,centre,boundry,reso)
    array_num = size(xt,1);
    kk = 0;
    for lk = centre-boundry/2:reso:centre+boundry/2
        kk = kk+1;
        a_hat = exp(-1i*(0:array_num-1)'*pi*sind(lk));
        music_val(kk) = norm(a_hat'*xt)^2;
    end
        lk = centre-boundry/2:reso:centre+boundry/2;
        [~,index_max] = sort(music_val,'ascend');
        theta = lk(index_max(1));
end

function [] = beam_plot(input_weight_vector)
    array_num = length(input_weight_vector);
    theta = -90:0.01:90;
    p = exp(-1j*2*pi*(0:array_num-1)'*sind(theta)/2);
    y = input_weight_vector'*p;
    outputval = 20*log10(abs(y)/max(abs(y)));
    figure()
    plot(theta,outputval,'LineWidth',2);
end

仿真运行结果如下所示：

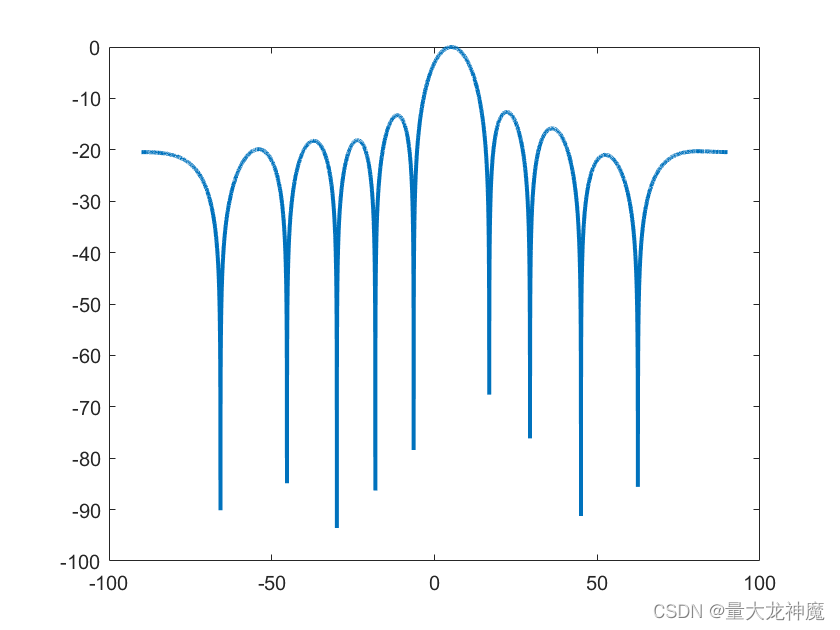
可以发现，线积分类算法在高斯噪声下具有着不错的性能。

参考文献

S. Mohammadzadeh, V. H. Nascimento, R. C. de Lamare and O. Kukrer. Covariance Matrix Reconstruction Based on Power Spectral Estimation and Uncertainty Region for Robust Adaptive Beamforming. IEEE Transactions on Aerospace and Electronic Systems.

2048 AI社区

有“AI”的1024 = 2048，欢迎大家加入2048 AI社区

更多推荐

UFW防火墙安全指南

UFW（Uncomplicated Firewall）是Ubuntu/Debian系统中简化防火墙管理的工具，通过直观命令帮助用户有效控制网络流量，提升系统安全性。文章详细介绍了UFW的基本命令，包括启停防火墙、添加规则、限制连接速率和日志配置等操作，并提供了安全最佳实践，如默认拒绝策略、IP地址限制和服务级规则管理。同时，还涵盖高级配置技巧，例如多网络接口设置、规则优先级调整、IPv6支持及与f