利用矩阵求斐波那契数列

flyfish 2015-8-27
矩阵（matrix）定义

一个m*n的矩阵是一个由m行n列元素排成的矩形阵列。矩阵里的元素可以是数字符号或者数学式.

形如

<script type="math/tex; mode=display" id="MathJax-Element-1">\begin{Bmatrix} a & b\\ c & d \end{Bmatrix}</script> 的数表称为 二阶矩阵，它由二行二列组成，其中a,b,c,d称为这个矩阵的元素。

形如

<script type="math/tex; mode=display" id="MathJax-Element-2">\begin{Bmatrix} x_1\\ x_2 \end{Bmatrix}</script>
的有序对称为 列向量Column vector

设

<script type="math/tex; mode=display" id="MathJax-Element-3">\begin{equation*}A=\begin{Bmatrix} a & b\\ c & d \end{Bmatrix} \end{equation*}</script>
<script type="math/tex; mode=display" id="MathJax-Element-4">\begin{equation*}X=\begin{Bmatrix} x_1\\ x_2 \end{Bmatrix} \end{equation*}</script>
则 <script type="math/tex; mode=display" id="MathJax-Element-5">\begin{equation*}Y= \begin{Bmatrix} ax_1+bx_2\\ cx_1+dx_2 \end{Bmatrix} \end{equation*}</script>
称为二阶矩阵A与平面向量X的乘积，记为AX=Y

斐波那契(Fibonacci)数列

从第三项开始，每一项都是前两项之和。
Fn <script type="math/tex" id="MathJax-Element-6">F_n</script>= Fn <script type="math/tex" id="MathJax-Element-7">F_n</script> − <script type="math/tex" id="MathJax-Element-8">_-</script> 1 <script type="math/tex" id="MathJax-Element-9">_1</script> + Fn <script type="math/tex" id="MathJax-Element-10">F_n</script> − <script type="math/tex" id="MathJax-Element-11">_-</script> 2 <script type="math/tex" id="MathJax-Element-12">_2</script>, n⩾3 <script type="math/tex" id="MathJax-Element-13">n\geqslant 3</script>

把斐波那契数列中 相邻的两项 Fn <script type="math/tex" id="MathJax-Element-14">F_n</script>和 Fn <script type="math/tex" id="MathJax-Element-15">F_n</script> − <script type="math/tex" id="MathJax-Element-16">_-</script> 1 <script type="math/tex" id="MathJax-Element-17">_1</script>写成一个2 × <script type="math/tex" id="MathJax-Element-18">\times</script>1的矩阵。
F0=0 <script type="math/tex" id="MathJax-Element-19">F_0=0</script>
F1=1 <script type="math/tex" id="MathJax-Element-20">F_1=1</script>

<script type="math/tex; mode=display" id="MathJax-Element-21">\begin{equation*} \begin{Bmatrix}F_n\\F_{n-1}\end{Bmatrix} \end{equation*}</script>
<script type="math/tex; mode=display" id="MathJax-Element-22">\begin{equation*} =\begin{Bmatrix}F_{n-1}+F_{n-2}\\F_{n-1}\end{Bmatrix} \end{equation*}</script>
<script type="math/tex; mode=display" id="MathJax-Element-23">\begin{equation*} =\begin{Bmatrix}1\times F_{n-1}+1\times F_{n-2}\\1\times F_{n-1}+0\times F_{n-2}\end{Bmatrix} \end{equation*}</script>

<script type="math/tex; mode=display" id="MathJax-Element-344">\begin{equation*} =\begin{Bmatrix}1&1\\1&0\end{Bmatrix}\times\begin{Bmatrix}F_{n-1}\\F_{n-2}\end{Bmatrix} \end{equation*}</script>
<script type="math/tex; mode=display" id="MathJax-Element-345">\begin{equation*} =\begin{Bmatrix}1&1\\1&0\end{Bmatrix}^{n-1}\times\begin{Bmatrix}F_{1}\\F_{0}\end{Bmatrix} \end{equation*}</script>
<script type="math/tex; mode=display" id="MathJax-Element-346">\begin{equation*} =\begin{Bmatrix}1&1\\1&0\end{Bmatrix}^{n-1}\times\begin{Bmatrix}1\\0\end{Bmatrix} \end{equation*}</script>

求F(n)等于求二阶矩阵的n - 1次方，结果取矩阵第一行第一列的元素。

问题转换为二阶矩阵的n次幂

二阶矩阵的乘法
设

<script type="math/tex; mode=display" id="MathJax-Element-347">\begin{equation*} A=\begin{Bmatrix} a & b\\ c & d \end{Bmatrix}, B=\begin{Bmatrix} e & f\\ g & h \end{Bmatrix}, 则 AB=\begin{Bmatrix} ae+bg & af+bh\\ ce+dg & cf+dh \end{Bmatrix} \end{equation*}</script>
矩阵A与矩阵B的积记做AB。

假设计算A的N次幂
方法1：
二阶矩阵的乘法满足结合律
设A,B,C都是任意的二阶矩阵
A(BC)=(AB)C

n=N/2 结果向下取整

AN=An∗An <script type="math/tex" id="MathJax-Element-348">A^{N}=A^{n}*A^{n} </script> 当n为偶数
AN=An∗An∗A <script type="math/tex" id="MathJax-Element-349">A^{N}=A^{n}*A^{n}*A </script> 当n为基数

相当于

A6=A3∗A3 <script type="math/tex" id="MathJax-Element-350">A^{6}=A^{3}*A^{3} </script>
A7=A3∗A3∗A <script type="math/tex" id="MathJax-Element-351">A^{7}=A^{3}*A^{3}*A </script>
这样可以减少计算次数
因为
A6=A∗A∗A∗A∗A∗A <script type="math/tex" id="MathJax-Element-352">A^{6}=A*A*A*A*A*A</script> 这里有5个乘
A6=（A∗A∗A）∗（A∗A∗A） <script type="math/tex" id="MathJax-Element-353">A^{6}=（A*A*A）*（A*A*A） </script> 计算完A*A*A 得到结果 A3 <script type="math/tex" id="MathJax-Element-354">A^{3}</script>
再乘以 A3 <script type="math/tex" id="MathJax-Element-355">A^{3}</script> 这里用了3个乘

方法2
以计算 A6 <script type="math/tex" id="MathJax-Element-356">A^{6}</script>为例
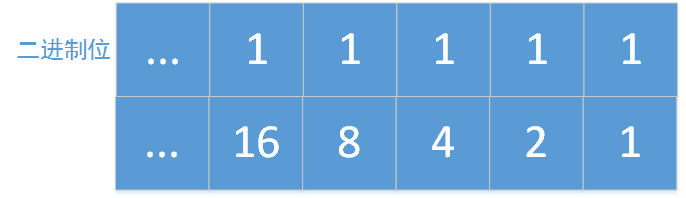
将6转化成二进制110
A6=A4∗A2 <script type="math/tex" id="MathJax-Element-357">A^{6}=A^{4}*A^{2}</script>

上图显示二进制与幂的指数关系
二进位为1需要乘，为0不需要乘

10进制7 = 二进制 111
例如 A7=A4∗A2∗A1 <script type="math/tex" id="MathJax-Element-358">A^{7}=A^{4}*A^{2}*A^{1}</script>
xie10进制31 = 二进制 11111
A31=A16∗A8∗A4∗A2∗A1 <script type="math/tex" id="MathJax-Element-359">A^{31}=A^{16}*A^{8}*A^{4}*A^{2}*A^{1}</script>

先写一个快速求幂的算法 该代码段是独立代码

#include <stdio.h>
//base 底数 ，exp 指数 
int qpow(int base,int exp)
{
if (0==exp ) return 1;

int ret=1;

while(exp)
{
    if(exp&1)//exp最右边一位 按位与&
    {
        ret=ret*base;
    }
    base=base*base;
    exp>>=1;//右移一位 
}
return ret;
} 

int main()
{
    printf("%d",qpow(3,5));
    return 0;
}

再写利用矩阵求斐波那契数列

#include<iostream>
using namespace std;
class Matrix
{
public:
    void Init()  
    {         
        e_[0][0]=1;
        e_[0][1]=1;
        e_[1][0]=1;
        e_[1][1]=0; 
    }
    void Unit() //单位矩阵 
    {   
        e_[0][0]=1;
        e_[0][1]=0;
        e_[1][0]=0;
        e_[1][1]=1;        
    }
public:  
   int Get() const
   {
   return e_[0][1];
   }
    friend Matrix operator*(const Matrix& A,const Matrix& B)
    {
        Matrix AB;   
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
        {   
            AB.e_[i][j]=0;
            for(int k=0;k<2;k++)
                AB.e_[i][j]+=A.e_[i][k]*B.e_[k][j];         
        }  
    return AB;
    }

private:
    __int64 e_[2][2];    

};

int qpow(Matrix& AB,int n) //矩阵快速幂 
{   
#define Bit(n) 1<<n
    Matrix t; 
    t.Init(); 
    for(int i=0;Bit(i)<=n;i++) 
    {   if(Bit(i)&n) AB=AB*t; 
        t=t*t;     
    }
    return AB.Get();    
}

调用方法

int n=10;
Matrix AB;
AB.Unit();
qpow(AB,n);//输出是55

代码中单位矩阵的解释
二阶方阵

<script type="math/tex; mode=display" id="MathJax-Element-426">\begin{equation*}\begin{Bmatrix} 1 & 0\\ 0 & 1 \end{Bmatrix} \end{equation*}</script>称为单位矩阵，通常记做E
对于任意二阶方阵A,都有 AE=EA=A
单位矩阵E在二阶方阵乘法的作用，相当于1在数的乘法中的作用。