（个人向小结，持续更新）

李雅普诺夫函数：

在一个球内，是正定的，有连续偏导数，且沿着系统任意状态轨线倒数为负半定，那么为系统的李雅普诺夫函数（Lyapunov function）。

 局部稳定性（local Stability）以及全局稳定性（Global Stability）均可以基于给出，其中局部稳定性约束较弱，只需要在一个球内，正定，负半定即可。可以直观看出，由于Ly函数的下降趋势，如果状态初值取一个稳定点附近合适大小，相应地状态后续变化也不会超过一个上界，即“稳定”的定义。特别的，如果负定，则0点（稳定点）是渐进稳定的（asymptotic stable），也很直观，导数为负，一直下降，直到趋于0.

全局稳定约束更强一点，需要将球放大到整个空间，任何与“无穷”这个概念扯上关系的理论，都要格外小心，全局稳定就需要增加径向无界（radial unboundedness）条件，即。相对而言，全局的渐近稳定性更加有意义，径向无界相当于通过约束边界性质（即不能V沿着||x||无穷大的方向有递减的趋势，不然对于全局而言，同样也会导致系统状态不收敛）。一般来说，做工程关注局部稳定性即可。

 对于非自治系统，需要变成，有着与以上类似的性质。此外，有大量的定理去减少特定情况下李雅普诺夫函数的保守性。

例1.分析系统（相应于物体在黏性的液体中下沉）的稳定性（来自于applied nonlinear control习题4.2）：

分析：系统一阶，有着简单的非线性，有经验的话看就能看出来是稳定的。可以基于状态平方构建李雅普诺夫函数，求导可以发现还是会对进行分析。所以，不如直接分析相图。

1).c>=0时，画抛物线，求根，有唯一稳定点，简单仿真一下，初值-10可以到计算的稳定点：

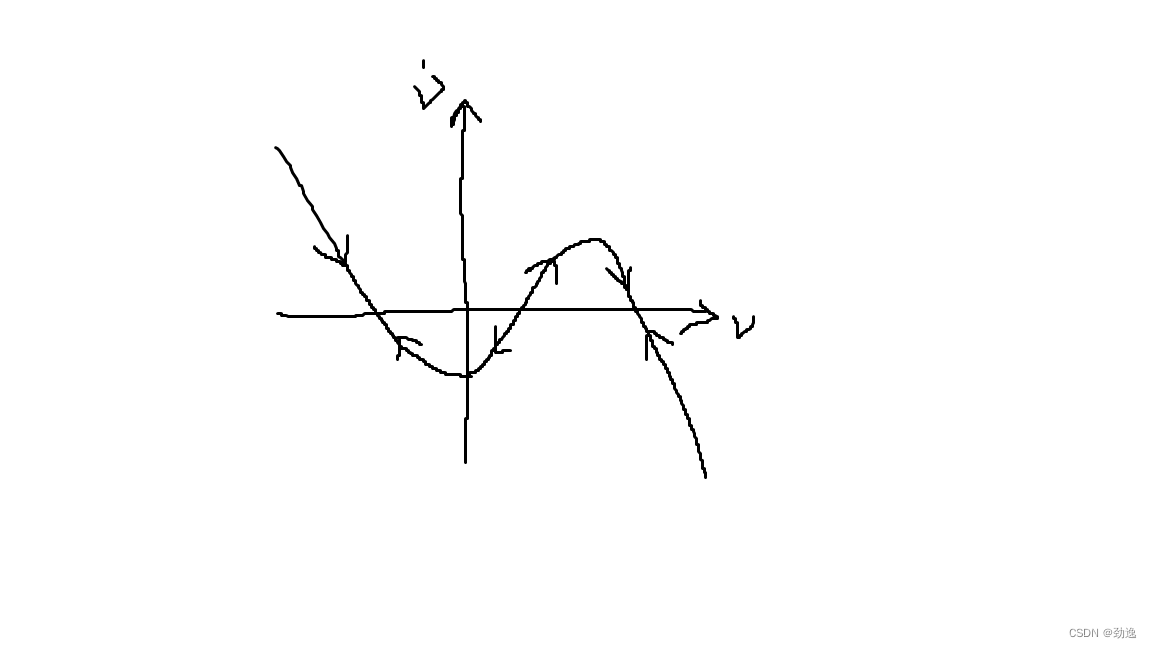
2).c<0时，有三个平衡点，两个稳定点；如果c特别大，会把抛物线拉下去，这时候就一个平衡点（稳定）。具体会收敛到哪里，初值有关

 李雅普诺夫函数:

上面提到均为自治系统，那么还有很多系统与时间函数g(t)有关，这种微分方程解析解很难获得。

此时李亚普诺夫函数往往会采取含有时间t的方式来构建，并与时不变的V(x)进行比较。

正定性：

这里强调的是与时不变函数做比较，判断正定，称为V(x,t) dominates V0(x)。（中文将dominate翻译为控制住，个人感觉不是很好，翻译为主导或者支配更好一点吧）。

无界性：

无界性就是找一个Vl(x) 来dominantes这个函数。

例2.说明LPV系统的稳定性：

这个例子可以看出来，虽然的特征值随时间增长，但是其依然全局渐近稳定，这说明特征值判据只能作为充分条件，特征值的dominate系统的动态还不够直接与强悍。

这个可以构建李雅普诺夫函数

求导，-dotV大于等于大于0，dotV负半定，全局渐近稳定