💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献 

🌈4 Matlab代码、数据、Simulink仿真、文章下载

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

内燃机排气管排放控制

问题描述
火花点火内燃机（SI ICE）是城市地区空气污染的主要原因之一。研究表明，如果能够将空燃比（lambda）控制在理论值1的±1%范围内，催化转化器几乎可以消除所有排放污染物。汽车行业主要依赖比例-积分（PI）控制器来调节lambda值。然而，PI控制器本质上是线性的，在非线性条件下无法提供鲁棒的性能。

在本项目中，我们设计并实现了模型预测控制（MPC），以将lambda值调节在理论值的±1%范围内。我们首先使用发动机在随机方波条件下的离线数据训练了一个神经网络，然后利用该神经网络开发了MPC。

摘要
理论空燃比（lambda）控制对三效催化剂在减少内燃机（ICE）尾气污染物排放中的性能起着重要作用。传统的控制器，如PI系统，无法在外部干扰和模型不确定性的情况下实现对lambda的鲁棒控制。因此，设计了一个模型预测控制（MPC）系统以实现对lambda的鲁棒控制。为了提供一个精确且面向控制的模型，开发了一个火花点火（SI）发动机的均值模型，用于生成发动机子系统的仿真数据。基于仿真数据，生成了两个发动机的神经网络模型。经过识别的多层感知器（MLP）神经网络模型相比自适应径向基函数（RBF）神经网络模型具有更小的验证误差。因此，基于MLP发动机模型，通过梯度下降算法中的非线性约束优化实现了MPC系统。MPC系统的性能与一阶滑模控制（SMC）系统进行了比较。根据仿真结果，MPC系统对lambda的跟踪精度接近SMC系统。然而，MPC系统产生的喷射燃油信号要平滑得多。  

1. 引言
内燃机是空气污染的主要原因之一。国家和国际法规，如车载诊断系统II（OBD II），由于其可能的致癌性和对人体组织的破坏性影响，限制了汽车行业排放污染物的精确预定义且严格的允许量[1]。内燃机排放的污染物，尤其是氮氧化物（NOx）、碳氢化合物（HC）和一氧化碳（CO），大多是致癌气体，还可能导致心脏病和呼吸系统疾病。幸运的是，通过使用三效催化转化器，这些污染物的排放量可以显著减少。

作为主要关注点，催化转化器在其最佳状态下能够有效工作，此时lambda值应被控制在理论值的±1%范围内 [1]。在汽车行业用于控制lambda的PI控制器需要经过长时间的校准过程，并且在存在外部噪声/干扰的情况下无法有效工作。此外，PI控制器对发动机参数的不确定性和时变动态的性能表现并不令人满意，缺乏鲁棒性 [2]。

如今，随着微计算机行业的进步，智能和自适应的lambda控制算法可以在发动机的电子控制单元（ECU）中实现。这些控制器不仅具有显著的瞬态和稳态性能，而且调整简单，对不确定性具有鲁棒性 [1]。

在面向控制的内燃机模型中，火花点火发动机的均值模型得到了发展。在均值发动机模型（MVEM）中，每个状态变量的动态方程被拟合到相应状态的均值。通过这种方式，模拟的真实发动机动态在稳态模式下能够得到与典型测功机测量一样精确的状态值，并在瞬态模式下产生2%的平均绝对误差（MAE） [3]。最初，由于发动机容积效率建模的困难，MVEM无法应用于新型火花点火发动机。Hendricks等人通过引入一个简单的容积效率模型改进了MVEM，从而使改进后的模型能够广泛应用于各种火花点火发动机 [4]。

2005年，Wang和Yu首次开发了基于神经网络的lambda模型预测控制（MPC），采用了一种具有在线和离线反向传播以及递归最小二乘训练算法的自适应多层感知器（MLP）神经网络系统。与离线训练方法相比，在线算法在平均绝对误差（MAE）意义上得到了更小的识别误差。由于神经网络模型是在输入变量的有限范围内进行训练的，因此MPC的预测控制通过约束优化算法获得。通过假设在整个预测范围内燃油喷射量为固定值，可以进行基于简化海森矩阵方法的约束优化。然而，这种方法给MPC算法带来了沉重的计算负担和二次规划 [5]。

Wang等人引入了一种基于二阶径向基函数（RBF）神经网络模型的识别方法，并将其应用于火花点火发动机的MPC。在预测范围内假设燃油喷射量为固定值的情况下，使用上述简化的海森矩阵方法进行约束优化。与PI控制器相比，基于RBF的MPC显示出对模型不确定性的高鲁棒性以及更好的瞬态性能 [6]。

Zhai和Yu使用自适应二阶RBF神经网络，并应用递归最小二乘算法进行RBF模型的在线训练。在固定燃油假设下，通过割线法和简化海森矩阵方法对引入的成本函数进行优化。

8. 结论  
作为一种替代传统PI控制器的方案，本文提出了一种基于多层感知器（MLP）神经网络识别的新型非线性模型预测控制（MPC）系统，用于火花点火发动机的理论空燃比控制。考虑到火花点火发动机的模型不确定性和时变动态特性，新的MPC系统以火花点火发动机的均值模型（MVEM）为控制导向模型，通过模拟生成了用于识别两种不同MLP和RBF神经网络系统的所需数据。根据验证结果，降低训练过程中数据采集的采样时间会显著提高识别精度。此外，与该研究领域记录的结果相比，通过更小的采样时间，获得了在lambda跟踪的平均绝对误差（MAE）意义上更好的控制性能。在实时实现方面，优化成本函数的预测范围已缩短为1，并采用了梯度下降算法作为一种简单且快速的优化方法。通过与一阶滑模控制（SMC）系统的比较，评估了MPC系统的性能。与SMC系统相比，所提出的MPC系统使得喷射燃油的变化更加平稳。

详细文章见第4部分下载。 

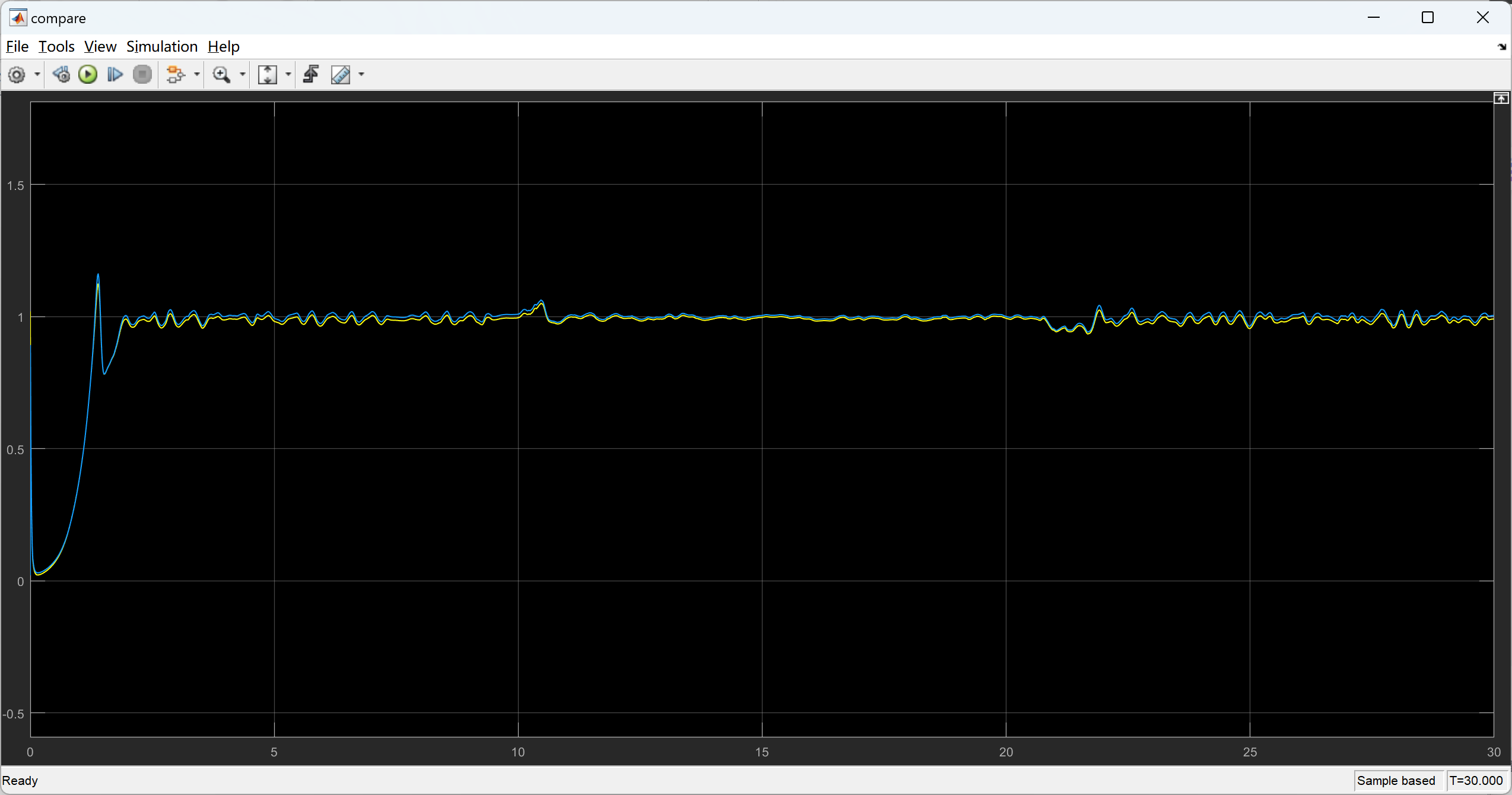
📚2 运行结果

部分代码：

%% engine parameters

alfa0=15*pi/180;  % Throttle plate closing angle
Pa=1.013;         % ambient pressure in bar
Vi=3*564e-6;      % intake manifold and port passage volume m^3
R=0.00287;        % gas global constant kj kg/k
Ta=293;           % ambient temperture k
Ti=308;           % intake manifold temperature k
mat1=5.9403;      % a parameter in finding m_at
mpTa=mat1*Pa/sqrt(Ta); % a parameter in finding m_at
mat0=0;           % a parameter in finding m_at
Vd=1.275;         % engine displacement liter
Ncyl=4;           % number of cylinders 
k=1.4; % 
Pc=.4125;         % a parameter (2/(k+1))^(k/(k-1));
si=.961;          % slope in volumetric efficiency 
yi=-0.07;         % bias in volumetric efficiency 
etaif2 = -0.015;
Lth=14.67;        % Stoichiometric AFR 
Hu=43000;         % Fuel heating value for gasoline kj/kg
Iac = 0.48;       % Moment of Inertia of engine
I = Iac*(2.0*pi/60)^2*1000;
kb2 = 0.470;
eta_var=.00010000;

%% neural network weights and bias terms 

% wieghts in the hidden layer of the neural network
W1 = [0.592914800842690	1.25815955137360	1.39919905554904	3.41285598808794
        -0.00871309626170767	-0.358389916615477	-0.285366031610041	-0.712989521257612
        -0.0163304117053378	-0.465960743474944	2.34625953956319	-2.16672891438372
        2.60879293016287	-0.980828607062894	-2.63663985586096	-1.31930727162727];

% wieghts in the output layer of the neural network 
W2= [0.0386   -0.8893    0.6852   -0.1763];

% bias in the first layer of the neural network
b1 =[   -4.3893
        0.3245
        0.1885
        4.7925];

% bias in the output layer of the neural network
b2 = 0.3742;

%% normalization paramters 

max_lambda =  1.1062; % max value of labmda used for normalization/denormalization
min_lambda =  0.0161;  % min value of labmda used for normalization/denormalization
max_m_dot =   0.0077; % max value of dot_m_fi used for normalization/denormalization
min_m_dot =   0.0012; % min value of dot_m_fi used for normalization/denormalization

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈4 Matlab代码、数据、Simulink仿真、文章下载

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取