参数化曲线——参数三次样条曲线(实例)
如何构造一条通过这些数据点并满足二阶连续的三次样条曲线?介绍了埃尔米特基形式的三次多项式曲线及其域变换。推导了满足二阶连续的条件——三切矢连续性方程。解矩阵,可求得每个数据点的切矢。介绍了数据点的参数化方法。介绍了样条曲线的边界条件。给定空间中n+1个数据点。
问题及相关理论
给定空间中n+1个数据点 p i ( i = 0 , 1 , . . . , n ) \bm{p}_i(i=0,1,... ,n) pi(i=0,1,...,n),如何构造一条通过这些数据点并满足二阶连续的三次样条曲线?
参数化曲线——参数三次样条曲线(1)介绍了数据点的参数化方法。
参数化曲线——参数三次样条曲线(2)介绍了埃尔米特基形式的三次多项式曲线及其域变换。
参数化曲线——参数三次样条曲线(3)推导了满足二阶连续的条件——三切矢连续性方程。
参数化曲线——参数三次样条曲线(4)介绍了样条曲线的边界条件。
实践
现应用以上理论进行实践:
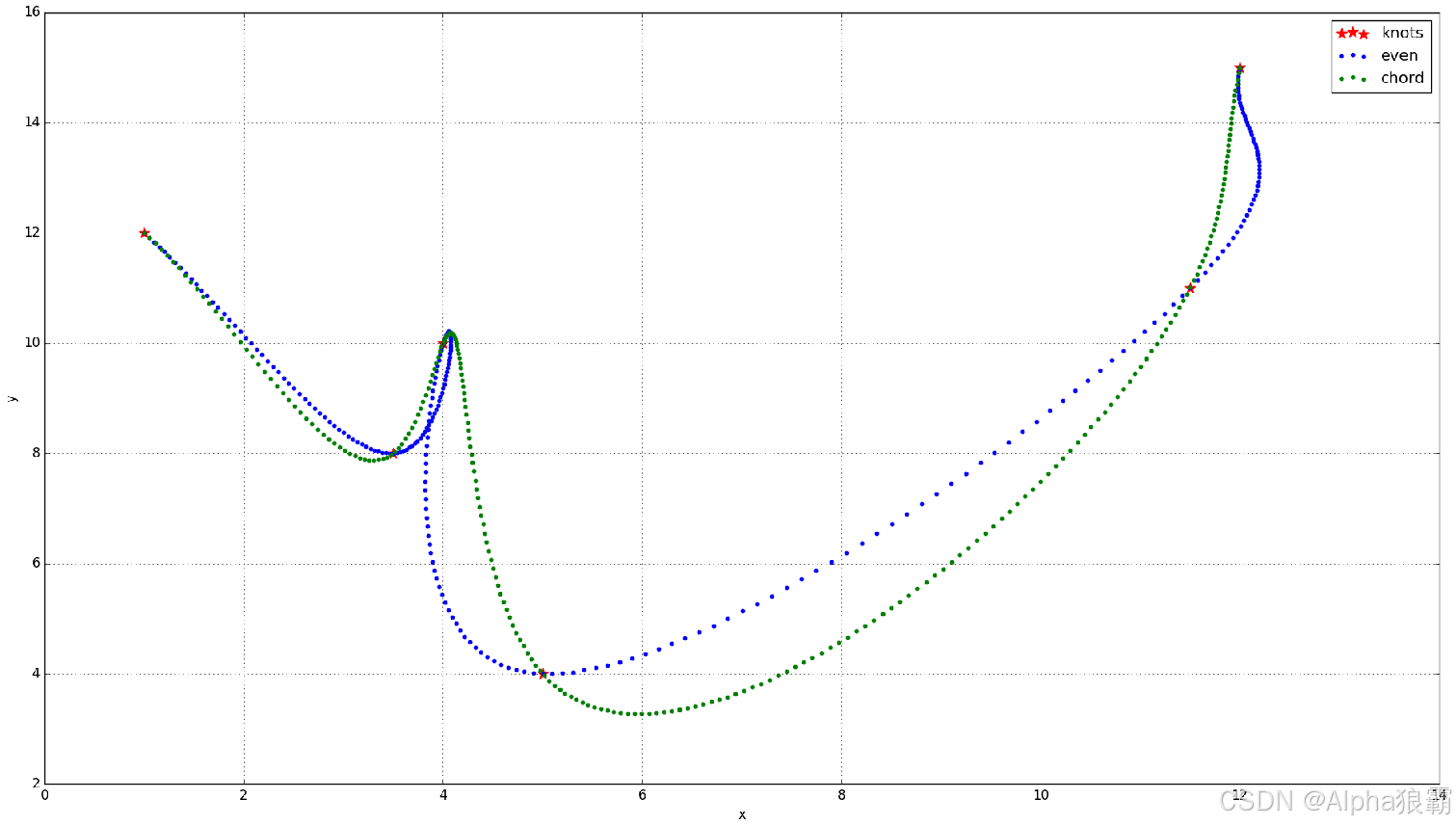
给定6个数据点 p 0 ( 1 , 12 , 0 ) \bm{p}_0(1, 12, 0) p0(1,12,0)、 p 1 ( 3.5 , 8 , 0 ) \bm{p}_1(3.5, 8, 0) p1(3.5,8,0)、 p 2 ( 4 , 10 , 0 ) \bm{p}_2(4, 10, 0) p2(4,10,0)、 p 3 ( 5 , 4 , 0 ) \bm{p}_3(5, 4, 0) p3(5,4,0)、 p 4 ( 11.5 , 11 , 0 ) \bm{p}_4(11.5, 11, 0) p4(11.5,11,0)、 p 5 ( 12 , 15 , 0 ) \bm{p}_5(12, 15, 0) p5(12,15,0)
1.数据点的参数化
采用积累弦长参数化法,首先计算总弦长:
L = ∣ p 1 − p 0 ∣ + ∣ p 2 − p 1 ∣ + ∣ p 3 − p 2 ∣ + ∣ p 4 − p 3 ∣ + ∣ p 5 − p 4 ∣ L=|\bm{p}_1-\bm{p}_0|+|\bm{p}_2-\bm{p}_1|+|\bm{p}_3-\bm{p}_2|+|\bm{p}_4-\bm{p}_3|+|\bm{p}_5-\bm{p}_4| L=∣p1−p0∣+∣p2−p1∣+∣p3−p2∣+∣p4−p3∣+∣p5−p4∣
然后计算每个点对应的参数:
u 0 = 0 , u 1 = u 0 + ∣ p 1 − p 0 ∣ L , u 2 = u 1 + ∣ p 2 − p 1 ∣ L u_0=0, \ \ \ \ u_1=u_0+\frac{|\bm{p}_1-\bm{p}_0|}{L}, \ \ \ \ u_2=u_1+\frac{|\bm{p}_2-\bm{p}_1|}{L} u0=0, u1=u0+L∣p1−p0∣, u2=u1+L∣p2−p1∣
u 3 = u 2 + ∣ p 3 − p 2 ∣ L , u 4 = u 3 + ∣ p 4 − p 3 ∣ L , u 5 = u 4 + ∣ p 5 − p 4 ∣ L u_3=u_2+\frac{|\bm{p}_3-\bm{p}_2|}{L}, \ \ \ \ u_4=u_3+\frac{|\bm{p}_4-\bm{p}_3|}{L}, \ \ \ \ u_5=u_4+\frac{|\bm{p}_5-\bm{p}_4|}{L} u3=u2+L∣p3−p2∣, u4=u3+L∣p4−p3∣, u5=u4+L∣p5−p4∣
2.确定边界条件
采用切矢条件确定首尾两端的切矢:
p ˙ 0 = p 1 − p 0 u 1 − u 0 \dot{p}_0=\frac{\bm{p}_1-\bm{p}_0}{u_1-u_0} p˙0=u1−u0p1−p0
p ˙ 5 = p 5 − p 4 u 5 − u 4 \dot{p}_5=\frac{\bm{p}_5-\bm{p}_4}{u_5-u_4} p˙5=u5−u4p5−p4
3.三切矢连续性方程
Δ i p ˙ i − 1 + 2 ( Δ i − 1 + Δ i ) p ˙ i + Δ i − 1 p ˙ i + 1 = 3 ( Δ i Δ p i − 1 Δ i − 1 + Δ i − 1 Δ p i Δ i ) i = 1 , 2 , 3 , 4 Δ i = u i + 1 − u i \Delta_i\dot{\bm{p}}_{i-1}+2(\Delta_{i-1}+\Delta_i)\dot{\bm{p}}_{i}+\Delta_{i-1}\dot{\bm{p}}_{i+1}=3(\Delta_i\frac{\Delta\bm{p}_{i-1}}{\Delta_{i-1}}+\Delta_{i-1}\frac{\Delta\bm{p}_{i}}{\Delta_{i}}) \\ i=1,2,3,4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Delta_i=u_{i+1}-u_i Δip˙i−1+2(Δi−1+Δi)p˙i+Δi−1p˙i+1=3(ΔiΔi−1Δpi−1+Δi−1ΔiΔpi)i=1,2,3,4 Δi=ui+1−ui
由4个三切矢连续性方程和2个边界条件方程,可得矩阵:
[ b 0 c 0 a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 a 4 b 4 c 4 a 5 b 5 ] [ p ˙ 0 p ˙ 1 p ˙ 2 p ˙ 3 p ˙ 4 p ˙ 5 ] = [ d 0 d 1 d 2 d 3 d 4 d 5 ] \begin{bmatrix}b_0 & c_0&& \\ a_1&b_1&c_1& \\ &a_2&b_2&c_2& & \\ & &a_3&b_3&c_3& \\ & & &a_4&b_4&c_4 \\ & & & & a_5&b_5 \\ \end{bmatrix}\begin{bmatrix}\dot{\bm{p}}_{0} \\ \dot{\bm{p}}_{1} \\ \dot{\bm{p}}_{2} \\ \dot{\bm{p}}_{3} \\\dot{\bm{p}}_{4} \\ \dot{\bm{p}}_{5} \\ \end{bmatrix}=\begin{bmatrix}{\bm{d}}_{0} \\ {\bm{d}}_{1} \\ {\bm{d}}_{2} \\ {\bm{d}}_{3} \\{\bm{d}}_{4} \\ {\bm{d}}_{5} \\ \end{bmatrix}
b0a1c0b1a2c1b2a3c2b3a4c3b4a5c4b5
p˙0p˙1p˙2p˙3p˙4p˙5
=
d0d1d2d3d4d5
其中,边界条件确定: b 0 = 1 , c 0 = 0 , d 0 = p ˙ 0 a 5 = 0 , b 5 = 1 , d 5 = p ˙ 5 b_0=1,c_0=0, \bm{d}_{0}=\dot{\bm{p}}_{0} \\ a_5=0,b_5=1, \bm{d}_{5}=\dot{\bm{p}}_{5} b0=1,c0=0,d0=p˙0a5=0,b5=1,d5=p˙5
三切矢连续性方程确定:
a i = u i + 1 − u i , i = 1 , 2 , 3 , 4 b i = 2 ( u i − u i − 1 ) + 2 ( u i + 1 − u i ) , i = 1 , 2 , 3 , 4 c i = u i − u i − 1 , i = 1 , 2 , 3 , 4 d i = 3 ( ( u i + 1 − u i ) p i − p i − 1 u i − u i − 1 + ( u i − u i − 1 ) p i + 1 − p i u i + 1 − u i ) , i = 1 , 2 , 3 , 4 a_i=u_{i+1}-u_i,\ \ \ \ \ i=1,2,3,4 \\ b_i=2(u_{i}-u_{i-1})+2(u_{i+1}-u_i),\ \ \ \ \ i=1,2,3,4 \\ c_i=u_{i}-u_{i-1},\ \ \ \ \ i=1,2,3,4 \\ \bm{d}_{i}=3((u_{i+1}-u_i)\frac{\bm{p}_i-\bm{p}_{i-1}}{u_i-u_{i-1}}+(u_{i}-u_{i-1})\frac{\bm{p}_{i+1}-\bm{p}_{i}}{u_{i+1}-u_{i}}),\ \ \ \ \ i=1,2,3,4 ai=ui+1−ui, i=1,2,3,4bi=2(ui−ui−1)+2(ui+1−ui), i=1,2,3,4ci=ui−ui−1, i=1,2,3,4di=3((ui+1−ui)ui−ui−1pi−pi−1+(ui−ui−1)ui+1−uipi+1−pi), i=1,2,3,4
4.矩阵运算
[ p ˙ 0 p ˙ 1 p ˙ 2 p ˙ 3 p ˙ 4 p ˙ 5 ] = [ b 0 c 0 a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 a 4 b 4 c 4 a 5 b 5 ] − 1 [ d 0 d 1 d 2 d 3 d 4 d 5 ] \begin{bmatrix}\dot{\bm{p}}_{0} \\ \dot{\bm{p}}_{1} \\ \dot{\bm{p}}_{2} \\ \dot{\bm{p}}_{3} \\\dot{\bm{p}}_{4} \\ \dot{\bm{p}}_{5} \\ \end{bmatrix}={\begin{bmatrix}b_0 & c_0&& \\ a_1&b_1&c_1& \\ &a_2&b_2&c_2& & \\ & &a_3&b_3&c_3& \\ & & &a_4&b_4&c_4 \\ & & & & a_5&b_5 \\ \end{bmatrix}}^{-1}\begin{bmatrix}{\bm{d}}_{0} \\ {\bm{d}}_{1} \\ {\bm{d}}_{2} \\ {\bm{d}}_{3} \\{\bm{d}}_{4} \\ {\bm{d}}_{5} \\ \end{bmatrix}
p˙0p˙1p˙2p˙3p˙4p˙5
=
b0a1c0b1a2c1b2a3c2b3a4c3b4a5c4b5
−1
d0d1d2d3d4d5
解矩阵,可求得每个数据点的切矢 p ˙ i ( i = 0 , 1 , 2 , 3 , 4 , 5 ) \dot{\bm{p}}_{i}(i=0,1,2,3,4,5) p˙i(i=0,1,2,3,4,5)
5.插值
给定一个参数 u ∈ [ 0 , 1 ] u\in[0,1] u∈[0,1],根据 u 0 , u 1 , u 2 , u 3 , u 4 , u 5 u_0,u_1,u_2,u_3,u_4,u_5 u0,u1,u2,u3,u4,u5确定其所处的段数,然后代入埃尔米特基方程计算该点:
p ( u ) = [ F i 0 ( u ) G i 0 ( u ) G i 1 ( u ) F i 1 ( u ) ] [ p i p ˙ i p ˙ i + 1 p i + 1 ] u ∈ [ u i , u i + 1 ] \bm{p}(u)=\begin{bmatrix}F_{i0}(u) & G_{i0}(u) & G_{i1}(u) & F_{i1}(u)\end{bmatrix}\begin{bmatrix}\bm{p}_i \\ \dot{\bm{p}}_i \\ \dot{\bm{p}}_{i+1} \\ \bm{p}_{i+1} \end{bmatrix} \qquad u\in[u_i,u_{i+1}] p(u)=[Fi0(u)Gi0(u)Gi1(u)Fi1(u)]
pip˙ip˙i+1pi+1
u∈[ui,ui+1]

更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)