【回归预测】GAM广义加性模型-MATLAB

随着大数据与人工智能技术的发展，回归分析已成为数据科学中的重要工具。它被广泛应用于多个领域，如金融预测、健康监测、工程系统控制等。广义加法模型（Generalized Additive Model, GAM）作为一种灵活的回归方法，能够有效捕捉输入变量与输出变量之间的非线性关系，是对传统线性回归模型的扩展。本文以广义加法模型为基础，通过MATLAB编程实现回归分析，并对其在数据预测中的应用进行详细

灵犀拾荒者

1494人浏览 · 2025-03-05 10:00:00

灵犀拾荒者 · 2025-03-05 10:00:00 发布

一、前言

二、技术与原理简介

广义加法模型（GAM）是一种非参数回归方法，旨在通过对输入特征进行非线性变换，来更灵活地建模预测问题。

1. 广义加性模型基础

广义加性模型是广义线性模型的扩展形式，其数学表达式为：

其中：𝑔(⋅) 为连接函数；𝑓𝑗(⋅) 为特征𝑋𝑗 的平滑函数；𝛽0 为截距项。

与传统线性模型相比，GAMs通过引入非线性平滑函数，能够捕捉变量间的复杂关系。每个特征分量𝑓𝑗 通常采用样条基函数表示：

式中𝜙𝑘(𝑥) 为基函数，常用B样条基或薄板样条基。基函数的数量𝐾 通过广义交叉验证（GCV）确定：

其中𝑆 为平滑矩阵；trace(S)表示模型复杂度。

2. 参数估计方法

模型参数估计采用惩罚似然法，目标函数为：

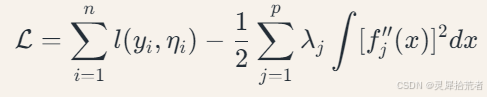
其中：𝑙(⋅) 为对数似然函数；𝜆𝑗 为平滑参数；积分项控制函数平滑度。

参数优化通过反向拟合算法实现，具体步骤为：

初始化截距项𝛽0=1𝑛∑𝑦𝑖
对每个特征分量𝑗j： a. 计算偏残差𝑟𝑗=𝑦−𝛽0−∑𝑘≠𝑗𝑓𝑘(𝑥𝑘)；b. 用平滑样条拟合𝑟𝑗∼𝑓𝑗(𝑥𝑗)
迭代直至收敛

三、代码详解

本文的 MATLAB 代码主要分为以下几个部分：

1. 数据加载与预处理

clear, clc; close all;
load data1 data1
N = length(data1);  
rng(7, 'twister')
temp = randperm(N);
ttt = 2; ppp = 950; f_ = ttt;
P_train = data1(temp(1:ppp), 1:ttt)';  % 获取训练集输入数据
T_train = data1(temp(1:ppp), 3)';        % 获取训练集目标数据
M = size(P_train, 2);

P_test = data1(temp(ppp+1:end), 1:ttt)'; % 获取测试集输入数据
T_test = data1(temp(ppp+1:end), 3)';       % 获取测试集目标数据
N = size(P_test, 2);

说明：

通过 load 加载数据，并利用 randperm 随机打乱顺序，确保样本的随机性。
按照预设的样本数（前 950 个为训练集，其余为测试集）划分数据。
数据转置后以列向量形式存储，便于后续矩阵计算。

2. 数据归一化及转置

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output); 

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

说明：

使用 mapminmax 函数将数据缩放到 [0,1] 区间，这有助于提高网络训练的稳定性和收敛速度。
分别对输入数据和目标数据进行归一化处理，后续在仿真测试时再将结果反归一化还原。

3. 模型创建与训练

%% 模型训练
Mdl= fitrgam(p_train,t_train); 	
Time=toc;

说明：

使用MATLAB的fitrgam函数训练广义加法回归模型。该函数通过最小化目标函数来优化平滑函数，使得模型能够适应数据的非线性关系。
使用训练数据p_train和t_train训练广义加法模型，并将训练好的模型存储在变量Mdl中。

4. 仿真测试与数据反归一化

%%  模型预测
t_sim1=predict(Mdl,p_train);  %训练集预测结果	
t_sim2=predict(Mdl,p_test);  %测试集预测结果			

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
T_sim1=T_sim1';T_sim2=T_sim2';

说明：

使用 predict 函数分别对训练集和测试集进行预测，获取模型输出。
通过 mapminmax('reverse', ...) 将归一化后的预测结果反归一化，恢复到原始数据尺度，便于与真实值比较。

5. 性能评价指标计算

%% 计算评价指标
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);  % 训练集 RMSE
error2 = sqrt(sum((T_test - T_sim2).^2) ./ N);     % 测试集 RMSE

R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2; % 训练集 R²
R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test))^2;      % 测试集 R²

mse1 = sum((T_sim1 - T_train).^2) ./ M;  % 训练集 MSE
mse2 = sum((T_sim2 - T_test).^2) ./ N;     % 测试集 MSE

SE1 = std(T_sim1 - T_train);
RPD1 = std(T_train) / SE1;               % 训练集剩余预测残差

SE = std(T_sim2 - T_test);
RPD2 = std(T_test) / SE;                 % 测试集 RPD

MAE1 = mean(abs(T_train - T_sim1));       % 训练集 MAE
MAE2 = mean(abs(T_test - T_sim2));        % 测试集 MAE

MAPE1 = mean(abs((T_train - T_sim1) ./ T_train)); % 训练集 MAPE
MAPE2 = mean(abs((T_test - T_sim2) ./ T_test));    % 测试集 MAPE

MBE1 = sum(T_sim1 - T_train) ./ M;        % 训练集 MBE
MBE2 = sum(T_sim2 - T_test) ./ N;         % 测试集 MBE

说明：

利用多种指标（RMSE、𝑅2 、MSE、RPD、MAE、MAPE、MBE）对模型在训练集和测试集上的表现进行定量评估。
决定系数 𝑅2 的计算公式为：

其中 𝑦𝑖 为实际值，𝑦^𝑖 为预测值，𝑦ˉ 为实际值的均值。

6. 完整代码

clear,clc;close all;tic
load data1 data1
rng(43,'twister')
N=length(data1);  
temp=randperm(N);
ttt=2;ppp=950;f_=ttt;
P_train = data1(temp(1: ppp), 1: ttt)';
T_train = data1(temp(1: ppp), ttt+1)';
M = size(P_train, 2);

P_test = data1(temp(ppp+1: end), 1: ttt)';
T_test = data1(temp(ppp+1: end), ttt+1)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output); 

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

%% 模型训练
Mdl= fitrgam(p_train,t_train); 	
Time=toc;

%%  模型预测
t_sim1=predict(Mdl,p_train);  %训练集预测结果	
t_sim2=predict(Mdl,p_test);  %测试集预测结果			

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
T_sim1=T_sim1';T_sim2=T_sim2';

%%  均方根误差 RMSE
error1 = sqrt(sum((T_sim1 - T_train).^2)./M);
error2 = sqrt(sum((T_test - T_sim2).^2)./N);
%% 决定系数
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test -  T_sim2)^2 / norm(T_test -  mean(T_test ))^2;
%% 均方误差 MSE
mse1 = sum((T_sim1 - T_train).^2)./M;
mse2 = sum((T_sim2 - T_test).^2)./N;
%% RPD 剩余预测残差
SE1=std(T_sim1-T_train);
RPD1=std(T_train)/SE1;
SE=std(T_sim2-T_test);
RPD2=std(T_test)/SE;
%% 平均绝对误差MAE
MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%% 平均偏差误差MBE
MBE1 = sum(T_sim1 - T_train) ./ M ;
MBE2 = sum(T_sim2 - T_test ) ./ N ;

四、总结与思考

本文通过详细的代码实现和分段讲解，展示了基于 MATLAB 平台的 BP 神经网络在数据拟合问题中的应用。实验结果表明，通过交叉验证确定最佳隐含层节点数，所构建的 BP 网络在训练集与测试集上均获得了较低的误差和较高的决定系数，表明其具备优秀的拟合能力和泛化性能。
从实际应用角度看，该方法为非线性数据建模提供了一种有效的解决方案，但仍需注意数据预处理、参数选择等环节对模型性能的影响。未来研究可进一步探讨网络结构改进、参数优化以及多模型集成等方向，以实现更高的预测精度和稳定性。

【作者声明】

通过本文的分析和实践，我们可以看到广义加法回归模型在回归问题中的巨大潜力。与传统的线性回归模型相比，广义加法回归模型具有更高的灵活性和解释性，能够有效处理输入变量与目标变量之间的非线性关系。通过使用MATLAB的fitrgam函数，我们能够方便地实现GAM模型，并通过多种评估指标对模型进行全面的性能评估。

然而，广义加法回归模型在实际应用中也面临着一些挑战，例如数据预处理的复杂性、正则化参数的选择等。因此，在实际应用中，如何有效选择模型的超参数和正则化方法，仍然是一个重要的研究方向。