2021SC@SDUSC

目录

介绍

错误学习

环形学习错误

同态操作

大致思路（重要）

加法

大致思路（重要）

 乘法

大致思路（重要）

---

介绍

在上一篇文章 PALISADE开源库（二）CKKS讲解系列（二）完整编码和解码 中，我们看到了如何实现CKKS的编码器和解码器，这使得我们能够将向量转化为多项式，反之亦然。这一步是必然的，因为我们将看到使用多项式要比直接使用向量更有效地构建同态加密方法。

我们将在本文中看到如何使用困难问题（例如LWE或RLWE）来构建近似同态加密方案。CKKS 使用近似算术而不是精确算术，从某种意义上说，一旦我们完成计算，我们可能会得到与直接进行计算的结果略有不同的结果。这意味着，如果您加密 2 和 3，添加它们的密文，然后解密，您可能会得到类似 4.99 或 5.01 而不是 5 的结果。 BFV 等其他方案是精确的，这意味着它们将产生恰好 5。

那么为什么要使用 CKKS 呢？CKKS 更适合实数算术，我们可以得到近似但接近的结果，而 BFV 更适合整数算术。

我们将在本文中看到如何使用 LWE 和 RLWE 实现近似算术同态加密方案的加密和解密。

错误学习

CKKS 是一种公钥加密方案，其中生成密钥和公钥。公钥用于加密，可以共享，私钥用于解密，必须保密。

CKKS和其他许多同态加密方案的基础是错误学习(LWE)问题，LWE问题是为了区分

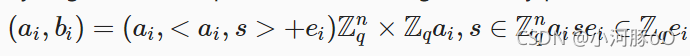
这个问题会变得容易得多，因为我们可以用高斯消去法来解线性方程组。

我们都知道，LWE问题的难度不亚于量子计算机的最坏情况格点问题。因此，我们可以利用发现秘密s(ai, < ai, s > +ei)这一事实。

假设我们生成一个秘钥：

 事实上，我们将使用 p = (-A.s + e, A) - A.s A.s

然后使用公钥和秘钥对一条μ∈Znq的消息进行加密和解密，可以采用以下方案:

• 使用p加密μ：输出

        c = (μ, 0) + p = (μ − A.s + e, A) = (c0, c1).

• 使用s解密c：输出

        μ' = c0 + c1.s = μ − A.s + e + A.s = μ+e ≈ μ

在加密阶段，我们使用公钥，用它来掩盖信息μ。因此，消息被隐藏在带有掩码−A.s的密文的第一个坐标中。记住A是均匀采样的，所以它确实有效地掩盖了μ。为了去掉它，我们可以使用c的第二个坐标，它只存储A，并与秘钥s结合，得到的解密结果是μ+e。注意这里，我们并没有精确地得到原始信息μ，而是μ加上一些噪声e，这就是为什么我们说我们有一个近似的算术方案。如果e足够小，则解密将接近于原始的μ。

因此，我们已经在这里看到了如何使用LWE问题来构建一个可以安全抵御量子攻击的公开加密方案。上述实现的问题是，虽然秘钥的大小是O(n)，但由于矩阵A，公钥的大小是O(n^2)，计算也需要O(n^2)操作。因为n将决定我们方案的安全性，如果我们使用LWE来构造我们的方案，在实践中它将非常低效，因为O(n^2)密钥大小和复杂性将使它太不切实际。

环形学习错误

环形学习错误是LWE的一个变体，但在环上。Znq不是使用向量，我们将工作在多项式Zq [X] / (X^N + 1)(我们假设这里N是2的幂)。现在我们画一个圆和e来自Zq [X] / (X^N + 1)，仍然是均匀采样的，圆是一个小秘密多项式和e是一个小噪声多项式。切换到RLWE有两个主要优点:

• 密钥的大小不再是二次的而是线性的，因为我们现在输出公钥p = (−a.s + e, a)，其中a.s表示a与s的多项式乘积。因为所有的操作都是在多项式之间完成的，所以私钥和公钥的大小都是O(n)。
• 乘法是在多项式上做的，因此它可以用离散傅里叶变换来完成复杂度为O(nlog(n))的多项式乘法，而不是O(n^2)因为我们必须做矩阵向量乘法。

所以用RLWE代替LWE，我们的key会小很多，运算会更快，所以前面的方案就更实用了。而且，RLWE 仍然是一个难题，并提供了强大的安全保证，因此使用 RLWE 仍然提供了一个安全方案。

同态操作

现在我们已经知道了为什么我们要研究Zq[X]/(X^N+1)的多项式，以及我们如何得到一个基于它的加密方案，让我们看看如何定义密文上的加法和乘法来得到一个同态加密方案。

我们有一个秘密为s，一个公钥p = (b, a)=(- a.s + e, a)，要加密消息μ，我们只需输出c = (μ+b, a)，而要用s解密它，我们计算c0+c1.s，它将近似地给出原始信息。

大致思路（重要）

加法

现在假设我们有两个信息：μ和μ'，然后我们把它们加密成c = (c0, c1)和c' =(c'0, c'1)。那么c'' = c + c' = (c0 + c'0, c1+c'1)就是 μ + μ'的正确加密，即当我们用s解密时，我们(近似地)得到μ+μ '。

实际上，c''的解密机制是c'',0+c'',1.s = c0 + c'0 + (c1 + c'1).s = c0 + c1.s + c'0 + c'1.s = μ+μ ' +2e≈μ+μ'。因为我们说过e是可以忽略的。

这意味着如果您添加密文，然后解密它们，您将获得添加的明文！这意味着通过这个简单的方案，您可以允许某人对加密数据执行添加操作，而用户仍然可以对其进行解密并获得正确的结果。这是我们迈向同态加密方案的第一步。

大致思路（重要）

 乘法

尽管如此，我们仍然需要定义密文上的乘法，这更复杂。实际上，我们的目标是找到一个密文堆积体c''，这样当我们用密钥s解密它时，我们就能得到明文的乘积。

因为两个密文的乘法比较复杂，所以我们现在先重点讲一个密文和一个明文的乘法，后面的文章看看密文之间的乘法怎么做。

假设我们有一个明文μ，加密成密文 c = (c0, c1)和明文μ'。然后，只需输出c'' = (μ'.c0，μ'.c1)，即可得到乘法的密文。

然后我们解密c''，我们得到：

μ′.c0 + μ′.c1.s=μ′.(c0 + c1.s)=μ′.(μ + e)=μ′.μ + μ′.e ≈ μ′.μ

因此，通过这些加法和乘法的实现，我们已经看到可以加密一些数据，对其执行操作，这样一旦我们解密它，我们就会得到与对明文数据执行计算相同的结果。

因为我们还有一些概念需要解决，比如密文-密文乘法、重新线性化和重新缩放，我们暂时不会介绍代码实现。一旦我们拥有了所有的构建块，我们将把所有东西放在一起，形成一个类似于 CKKS 的端到端近似同态加密方案！

大致思路（重要）