应用光学笔记02---共轴球面系统的物像关系

把透镜、反射镜、棱镜和光阑等各种光学零件按一定方式组合起来，满足一定要求的系统称为光学系统。按照有无对称轴可以分为共轴光学系统和非共轴光学系统，按照介质分界面形状分为球面光学系统和非球面光学系统。绝大多数光学系统都是共轴球面系统和平面镜、棱镜系统。本文推导了共轴球面系统的物像关系式，用以计算光学系统相应的物像位置和大小。

胖胖笔记

6821人浏览 · 2024-10-19 19:54:56

胖胖笔记 · 2024-10-19 19:54:56 发布

一、光学系统与成像的概念

1、光学系统

把各种光学零件（透镜、反射镜、棱镜和光阑等）按一定方式组合起来，满足一定要求的系统。如下图双目望远镜

按照有无对称轴可以分为共轴光学系统（系统具有一条对称轴线，光轴）和非共轴光学系统，按照介质分界面形状分为球面光学系统（系统中光学零件均由球面构成）和非球面光学系统。

绝大多数光学系统都是共轴球面系统和平面镜、棱镜系统。

2、成像的概念

（1）透镜类型

正透镜：凸透镜，中间厚边缘薄，使光线会聚（出射光线相对于入射光线向光轴方向折转），也叫聚焦透镜。如下图（a）。

负透镜：凹透镜，中心薄边缘厚，使光线发散（出射光线相对于入射光线向远离光轴方向折转），也叫发散透镜。如下图（b）。

（2）透镜作用---成像

A称为物点， $A'$ 点称为物体A通过透镜所成的像点。A和 $A'$ 称为共轭点，互为物像关系，在几何光学中称为“共轭”。

透镜成像原理

正透镜：中心比边缘厚，光束中心部分走的慢，边缘走得快。如下图所示，正透镜将向左弯曲的球面波POQ变为向右弯曲的球面波 $P'O'Q'$ ，所以物点A发出的光线经过透镜后会聚于像点 $A'$ ，成实像。

负透镜：边缘比中心厚，光束中心部分走的快，边缘走得慢。如下图所示，负透镜使出射波面更加弯曲，发散光线反向延长线上存在一个虚像点。

基本定义

像：出射光线的交点，如下图 $A'$

实像点：出射光线的实际交点，如图(a) $A'$

虚像点：出射光线延长线的交点，如图(b) $A'$

物：入射光线的交点，如下图A

实物点：实际入射光线的交点，如图(a) A

虚物点：入射光线延长线的交点，如图(b) A

像空间：像所在空间

实像空间：系统最后一面以后的空间，如图(a)透镜后曲面以后的空间。

虚像空间：系统最后一面以前的空间，如图(a)透镜后曲面以前的空间。

物空间：物所在空间

实物空间：系统第一面以前的空间，如图(a)透镜前曲面以前的空间

虚物空间：系统第一面以后的空间，如图(a)透镜前曲面以前的空间

物空间折射率：按实际入射光线所在空间折射率计算

像空间折射率：按实际出射光线所在空间折射率计算

二、共轴球面光学系统的物像关系式

共轴球面系统：系统中光学零件均由球面构成且具有对称轴的光学系统，如下图所示。

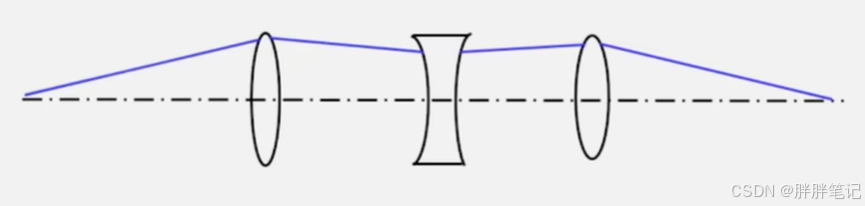
想要计算其物像关系式，首先需要推导出单个球面折射时，由入射光线位置计算出射光线位置的公式

1、单个折射球面光路计算公式

已知：入射光线位置L，U；光学系统r，n， $n'$ 。求通过单个折射球面后折射光线位置（根据折射定律 $nsinI=n'sinI'$ 推导）

(1)符号规则

线段：由左向右为正，由下向上为正，反之为负。

$L,L'$ ：球面顶点到光线与光轴交点；

$r$ ：球面顶点到球心；

$d$ ：前一面顶点到下一面顶点。

角度：顺时针转为正，逆时针转为负。

$U,U'$ ：光轴转到光线；

$I,I'$ ：光线转到法线；

$\varphi$ ：光轴转到法线

几何图形上各量标注其绝对值，永远为正，如下图所示。

（2）光路计算公式

推导过程：

2、多个球面共轴系统---转面公式

多个球面得共轴系统，前一个球面得出射光线为下一个球面得入射光线。由于球面位置改变，需要进行坐标转换---转面公式

$U_2=U_1' , L_2=L_1'-d_1$

3、近轴光学的物像基本式

1）近轴的定义

已知A距第一面顶点的距离为100，A点所发出的三根光线坐标分别为 $L_1=-100,U_1=-1^{\circ};L_2=-100,U_2=-2^{\circ};L_3=-100,U_3=-3^{\circ};$

运用共轴球面系统的光路计算公式可得到：

三根光线对应的 $L'$ 随着入射角U的增大而减小；U越小， $L'$ 变化越慢，由此定义靠近光轴的区域称为近轴区域， $U,U',I,I'$ 都很小，由此可将物像基本式改写，得到近轴光路光路计算公式：

转面公式

轴上物点用近轴光线成像符合理想成像，推导如下： $l$

轴外点B位于近轴区域，用近轴光线成像时，像点 $B'$ 位于B点和球心的连线上（辅助轴），也符合理想成像

2）物像位置关系式

近轴区域内成像近似符合理想，每个物点对应一个像点。由此只要物距 $l$ 确定，就可以利用近轴光路计算公式得到 $l'$ ，把像点位置 $l'$ 直接表示成物点位置 $l$ 和球面半径 $r$ 以及介质折射率 $n,n'$ 的函数 $l'=f(n,n',r,l)$

引入以光轴为计算起点到光线在球面的投射点的距离--- $h$ ，使光线坐标 $L,L',u,u'\rightarrow h,u,u'$

将公式 $i=\frac{l-r}{r}u$ 展开移项得 $u=-i+\frac{lu}{r}$ ①

由 $l'=r+\frac{ri'}{u'}$ 得 $u'=i'+\frac{l'u'}{r}$ ②

把 $h=lu=l'u'$ 代入①式并在其两边同时乘以 $n$ ，代入②式并在其两边同时乘以 $n'$ 可得

$nu=-ni+\frac{nh}{r}$ 和 $n'u'=n'i'+\frac{n'h}{r}$ ，两式相减并考虑近轴范围内 $ni=n'i'$ 得

$n'u'-nu=\frac{h}{r}(n'-n)$ ③

转面公式

$\left\{\begin{matrix}u_1=u_2 & \\ l_2=l_1-d_1 & \end{matrix}\right.\Rightarrow \left\{\begin{matrix}u_1=u_2 & \\ h_2=h_1-d_1u_1 & \end{matrix}\right.$

把③式两侧同时除以h得 $\frac{n'u'}{h}-\frac{nu}{h}=\frac{n'-n}{r}$ ，将 $\frac{nu}{h}=\frac{1}{l},\frac{u'}{h}=\frac{1}{l'}$ 代入得物像位置关系式

$n(\frac{1}{l}-\frac{1}{r})=n'(\frac{1}{l'}-\frac{1}{r})$

$\frac{n'}{l'}-\frac{n}{l}=\frac{n'-n}{r}$

3）物像大小关系式

用 $y$ 和 $y'$ 表示物点和像点到光轴的距离。位于光轴上方为正，反之为负

垂直放大率 $\beta=\frac{y'}{y}$

由图知 $\beta=\frac{y'}{y}=\frac{l'-r}{l-r}$ ，

由物像位置关系式 $n(\frac{1}{l}-\frac{1}{r})=n'(\frac{1}{l'}-\frac{1}{r})$ 移项通分得 $n'\frac{l'-r}{l'}=n\frac{l-r}{l}$ 代入上式得物像大小关系式

$\beta=\frac{y'}{y}=\frac{nl'}{n'l}$

利用公式可由任意位置和大小得物体，求得通过单个折射球面后近轴像的大小和位置；对于若干个透镜组成的共轴球面系统，逐面应用公式，可以求得任意近轴像的位置和大小。转面公式变为：

$l_2=l_1'-d,y_2=y_1'$

4）近轴光学公式的作用

第一，作为衡量实际光学系统成像质量的标准。用近轴光学公式计算的像，称为实际光学系统的理想像

第二，用它近似地表示实际光学系统所成像的位置和大小

因此可以把近轴光学公式扩大应用到任意空间

三、共轴理想光学系统

1、理想像和理想光学系统

1）基本概念

理想像：符合点对应点，直线对应直线，平面对应平面的像

共线成像：符合点对应点，直线对应直线，平面对应平面的成像变换

理想光学系统：能够成理想像的光学系统

2）理想成像

理想成像的条件：物点和像点之间所有光线的光程都相等。

等光程的反射面---二次曲面

(1)椭圆面：对两个定点距离之和为常数的点的轨迹，是以该两点为焦点的椭圆。对两个焦点符合等光程条件。

（2）双曲面：到两个定点距离之差为常数的点的轨迹，是该两点为焦点的双曲面。对内焦点和外焦点符合等光程条件。一个为实一个为虚

（3）抛物面：到一条直线和一个定点的距离相等的点的轨迹，是以该点为焦点，该直线为准线的抛物面。对焦点和无限远轴上点符合等光程。

3）共轴理想光学系统成像性质：

（1）轴上点成像在轴上

（2）位于过光轴某一截面内的物点对应像点位于同一平面内。如下图截面O上物点A、B与对应像平面 $O'$ 上像点 $A',B'$ 位于一个平面内。

(3)过光轴任意截面内成像性质相同---空间问题简化为平面问题，光学系统可以用过光轴的一个截面来代表

（4）物平面垂直光轴时，像平面也垂直于光轴

（5）物平面垂直于光轴时，物与像完全相似（相似：物平面无论什么部位的像都是按照同一放大率成像。定义放大率为像与物的比值 $\beta=\frac{y'}{y}$ ）

（6）已知两对共轭面的位置和放大率，或者一堆共轭面的位置和放大率，以及轴上两对共轭点的位置，则其任意物点的像点可以根据这些已知共轭面和共轭点来求得。光学系统成像性质可由这些基点和基面求得。

2、共轴理想光学系统

1）主平面和基点

由近轴光学的物像关系式可知不同位置的共轭面对应着不同的放大率

（1）放大率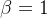 $\beta=1$ 的一对共轭面称为主平面。

这对共轭面的物平面称为物方主平面，这对共轭面的像平面称为像方主平面。两主平面与光轴的交点分别成为物方主点和像方主点，用 $H,H'$ 表示。

主平面性质：任意一条入射光线与物方主平面的交点高度和出射光线与像方主平面的焦点高度相同，如 $BH=B'H'$ 。

(2)无限远轴上物点和它所对应的像点 $F'$ ----像方焦点

光轴上点所发出光线：用光线与光轴交点到球面顶点距离L和入射光线与光轴的夹角U表示。物体距离光学系统越远，L长度增加，U角减小。物体趋于无限远时，U=0°，光线与光轴平行。

无限远轴上物点：用一束与光轴平行的光线表示

无限远轴外物体：用一束与光轴成一定夹角的平行光线表示

像方焦点：当轴上物点位于无限远时，像点 $F'$ 所在位置，如下图 $F'$ 。

像方焦平面：通过像方焦点垂直于光轴的平面称为。

性质：

①平行与光轴入射的任意光线，其共轭光线（出射光线）一定通过焦点，如下图左侧图；

②和光轴成一定夹角的平行光线通过光学系统后，必交于像方焦平面上一点，如下图右侧图

(3)无限远轴上像点和它所对应的物点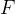 $F$ ----物方焦点

物方焦点：共轭像点位于轴上无线远的轴上物点，如下图F。

物方焦平面: 通过物方焦点垂直于光轴的平面

性质：

①过物方焦点入射的光线，通过光学系统后平行于光轴出射，如下图左侧图

②由物方焦平面上轴外任意一点发出的所有光线，通过光学系统后，对应一束与光轴成一定夹角的平行光线，如下图右侧图。

（4）焦距---主平面和焦点之间的距离

像方焦距：由像方主点 $H'$ 到像方焦点 $F'$ 的距离，用 $f'$ 表示。

物方焦距：由物方主点 $H$ 到物方焦点 $F$ 的距离，用 $f$ 表示。

$f',f$ 符号规则：以主点为起点，计算到焦点，由左向右为正。

可用一对主平面和两个焦点位置来代表一个光学系统，如下图

主平面和焦点是特殊的理想物像面/点，其位置可以采用近轴物像关系式求出

（5）共轴球面系统的主平面和焦点

单个折射球面的主平面和焦点

主平面 $\beta=\frac{nl'}{n'l}=1\rightarrow \Rightarrow nl'=n'l$ ，将其代入近轴物像位置关系式 $\frac{n'}{l'}-\frac{n}{l}=\frac{n'-n}{r}$ 得

$l=0,l'=0$ 。

球面得两个主点与球面顶点重合。物方主平面和像方主平面为过球面顶点得切平面

像方焦点对应 $l=\infty ,l'=f'$ ，物方焦点对应 $l'=\infty ,l=f$

应用近轴物像位置关系式 $\frac{n'}{l'}-\frac{n}{l}=\frac{n'-n}{r}$ 得

球面焦距公式 $f'=\frac{n'r}{n'-n}$ ， $f'=-\frac{nr}{n'-n}$

球面反射看作 $n'=-n$ 的折射，则 $f'=f=\frac{r}{2}$

共轴球面系统的焦点：平行于光轴入射的光线，通过光学系统后，出射光线与光轴的焦点就是像方焦点 $F'$ 。如果知道入射光束和光学系统参数 $(n_1,n_2,...n_k,r_1,r_2,...r_k,d_1,d_2,...d_k)$ ，，可由近轴光路计算公式逐面计算，求出最终出射光线坐标，进而求出焦点坐标。

如图所示，追迹一根平行光轴入射的光线，通过k个表面折射后，出射光线与光轴交点就是系统像方焦点 $F'$ 。

近轴光路计算公式，当 $l=\infty ,u=0$ 时，第一式无法使用，采用 $h,u$ 表示入射光线坐标 $i_1=\frac{h_1}{r_1}$ ，如下图所示

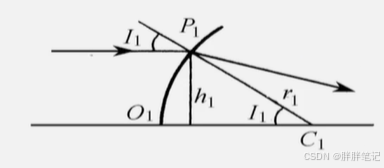
近轴光路计算公式变为 $\begin{matrix}i=\frac{h}{r} \\ i'=\frac{n}{n'}i \\ u'=u+i-i' \\ l'=r+\frac{i'}{u}r \end{matrix}$ ，转面公式变为 $\begin{matrix} u_2=u_1\\ h_2=h_1-d_1u_1 \end{matrix}$

逐面计算最后求得出射光线坐标 $u_k',l_k'$ ，如图所示

像方焦点 $F'$ 离最后一面顶点 $O_k$ 的距离 $l_k'$ ，称为像方顶焦距，由此像方焦点位置找出，求出像方焦距即可找出像方主平面。

由主平面性质(之前内容)可知，延长入射光线和出射光线，其焦点必定在像方主平面上。

由此可得焦距公式 $f'=\frac{h_1}{u_k'}$

将光学系统翻转，按计算像方焦点和像方主平面同样的方法，计算出结果就是物方焦点和物方主平面，如下图

第一面顶点O到物方焦点F的距离 $l_F$ 称为物方顶焦距

2）共轴理想光学系统的物像关系式

（1）牛顿公式

物点和像点位置坐标：

$x$ -----以物方焦点F为原点到物点A的距离

$x'$ ----以像方焦点 $F'$ 为原点到像点 $A'$ 的距离

由 $\Delta ABF\sim \Delta HIF$ 和 $\Delta H'K'F'\sim \Delta A'B'F'$ 得

牛顿物像大小关系式---垂直放大率 $\beta=\frac{y'}{y}=-\frac{f}{x}=-\frac{x'}{f'}$

交叉相乘后得到牛顿物像位置关系式--- $xx'=ff'$

上面两个式子就为牛顿公式

（2）高斯公式

物点和像点位置坐标：

$l$ -----以物方主点H为原点到物点A的距离

$l'$ ----以像方主点 $H'$ 为原点到像点 $A'$ 的距离

将关系 $x=l-f,x'=l'-f'$ 代入牛顿公式可以得出高斯公式

高斯物像位置关系式--- $\frac{f'}{l'}+\frac{f}{l}=1$

高斯物像大小关系式--- $\beta=\frac{y'}{y}=-\frac{x'}{f'}=-\frac{l'-f'}{f'}=1-\frac{l'}{f'}=-\frac{fl'}{f'l}$

3）光学系统的放大率

（1）垂轴放大率 $\beta=\frac{y'}{y}=-\frac{f}{x}=-\frac{x'}{f'}=-\frac{fl'}{f'l}$

垂轴放大率是共轭面像高与物高之比

牛顿公式表达形式： $\beta=-\frac{f}{x}=-\frac{x'}{f'}$

高斯公式表达形式 $\beta=-\frac{fl'}{f'l}$ ，

可以看出垂轴放大率与物距和相距有关

（2）轴向放大率 $\alpha=\frac{dx'}{dx}=-\frac{x'}{x}=-\frac{fl'^2}{f'l^2}$

当物平面沿光轴移动微小距离 $dx$ ，像平面相应移动 $dx'$ ，比例 $\frac{dx'}{dx}$ 称为光学系统的轴向放大率

对牛顿公式中 $xx'=ff'$ 取微分得到 $x'dx+xdx'=0$ ，由此得到

$\alpha=\frac{dx'}{dx}=-\frac{x'}{x}$

对高斯公式中 $\frac{f'}{l'}+\frac{f}{l}=1$ 取微分得到 $-\frac{f'}{l'^2}dl'-\frac{f}{l^2}dl=0$ ，由此得到

$\alpha=\frac{dx'}{dx}=\frac{dl'}{dl}=-\frac{fl'^2}{f'l^2}$

可以看出轴向放大率与物距和相距有关

（3）角放大率 $\gamma=\frac{tgU'}{tgU}=\frac{l}{l'}$

角放大率是轴上点A发出的光线通过光学系统后，出射光线与光轴夹角 $U'$ 的正切和对应的入射光线与光轴所形成的夹角U的正切之比。

对于近轴光学， $U,U'$ 趋近于0，角放大率公式 $\gamma=\frac{u'}{u}$

由图可知 $tgU=\frac{h}{l}$ ， $tgU'=\frac{h}{l'}$ 代入角放大率定义式得 $\gamma=\frac{tgU'}{tgU}=\frac{l}{l'}$

角放大率只和 $l,l'$ 有关，其大小仅取决于共轭面位置，与光线的会聚角无关，所以它与近轴光线角放大率相同。

牛顿公式： $\gamma=-\frac{f}{f'}\frac{1}{\beta}=\frac{x}{f'}=\frac{f}{x'}$

三个放大率的关系：对比 $\beta=-\frac{fl'}{f'l}$ ， $\alpha=-\frac{fl'^2}{f'l^2}$ ， $\gamma=\frac{l}{l'}$ 可以发现 $\beta=\alpha\gamma$

4）物像空间不变式---拉格朗日-亥姆霍兹不变式

代表实际光学系统在近轴范围内成像的一种普偏特性

对于单个折射球面，

由图可知 $u=\frac{h}{l},u'=\frac{h}{l'}$ ，两式相比可以得到 $\frac{u}{u'}=\frac{l'}{l}$ ，将其代入物像大小位置关系式 $\beta=\frac{y'}{y}=\frac{nl'}{n'l}$ ，可以得到

$nuy=n'u'y'$

对于多个折射球面构成的共轴系统

$n_i'=n_{i+1}',y_i'=y_{i+1},u_i'=u_{i+1}$

由此得到

$n_1u_1y_1=n_1'u_1'y_1'=n_2u_2y_2=...=n_k'u_k'y_k'$

结论：对于任意空间来说，乘积nuy总是一个常数，用J表示， $J=nuy=n'u'y'$ ---物像空间不变式

对于理想光学系统，

由角放大率 $\gamma=\frac{tgU'}{tgU}=\frac{u}{u'}$ 得 $n \cdot tgU \cdot y=n' \cdot tgU' \cdot y'$ ---理想光学系统物像空间不变式

5）物方焦距和像方焦距得关系式---化简物像关系式

对于单个折射球面，球面焦距公式 $f'=\frac{n'r}{n'-n}$ ， $f'=-\frac{nr}{n'-n}$ 。

由此可得 $\frac{f'}{f}=-\frac{n'}{n}$

对于理想光学系统，

由物像空间不变式 $\beta=\frac{y'}{y}=\frac{nu}{n'u'}$ 和垂轴放大率公式 $\beta=-\frac{fl'}{f'l}$ 得 $-\frac{fl'}{f'l}=\frac{nu}{n'u'}$

由图可知 $\gamma=\frac{tgU'}{tgU}=\frac{u}{u'}=\frac{l}{l'}$ ，将 $\frac{u}{u'}=\frac{l}{l'}$ 代入上式化简得到 $\frac{f'}{f}=-\frac{n'}{n}$

结论：一个光学系统得像方焦距和物方焦距之比等于像空间和物空间介质折射率之比，但符号相反。 $\frac{f'}{f}=-\frac{n'}{n}$

空气中， $f'=-f$ ，相应得物像关系式可以简化为：

物像位置公式

牛顿公式： $xx'=-f'^2$

高斯公式： $\frac{1}{l'}-\frac{1}{l}=\frac{1}{f'}$

放大率公式

垂轴放大率： $\beta=\frac{l'}{l}$

轴向放大率： $\alpha=\frac{l'^2}{l^2}$

角放大率公式不变 $\gamma=\frac{l}{l'}$

三种放大率之间的关系 $\beta=\frac{1}{\gamma},\alpha=\frac{\beta}{\gamma}=\beta^2$

6）节平面和节点

根据 $\gamma=\frac{tgU'}{tgU}=\frac{l}{l'}$ 和 $\gamma=\frac{x}{f'}=\frac{f}{x'}$ ，角放大率等于1的一对共轭面称为节平面。这对共轭面的物平面称为物方节平面，这对共轭面的像平面称为像方节平面。两主平面与光轴的交点分别成为物方节点和像方节点，用 $J,J'$ 表示。

性质：凡过物方节点J的光线，其出射光线必经过像方节点 $J'$ ，并且和入射光线相平行。如图所示

节点位置：

根据 $\gamma=\frac{x}{f'}=\frac{f}{x'}=1$ 可得 $x_J=f',x_J'=f$ 。如果物像空间介质相等，有 $f'=-f$ , $x_J=-f,x_J'=-f'$ ，在图中标出位置，可以发现之平面和节平面重合。如下图所示

$J'F'$

应用：

作图法求理想像时，可用来作第三条特殊光线。

测基点位置：光学系统绕像方节点 $J'$ 轴线摆动时，出射光线 $J'F'$ 的方向和位置不会因光学系统的摆动而发生改变；像点是所有出射光线的交点，必然在 $J'F'$ 上，所以像点不会随被测系统的摆动而摆动。如图

如果不饶 $J'$ 摆动，如下图绕J摆动，像跟随摆动。

因此，制作了周视照相机，如下图

7）物高和像高计算公式

（1）有限远物体对应像高计算公式

已知主面，焦点和焦距，利用高斯公式或者牛顿公式：

$\beta=\frac{y'}{y}=-\frac{f}{x}=-\frac{x'}{f'}$ 和 $\beta=\frac{y'}{y}=-\frac{fl'}{f'l}$

已知具体结构参数，半径，厚度，折射率，则追迹轴上的近轴光线

$\beta=\beta1 \cdot\ \beta2 \cdot \cdot \cdot \beta_k=\frac{n_1u_1}{n_1'u_1'} \cdot \frac{n_2u_2}{n_2'u_2'} \cdot \cdot \cdot \frac{n_ku_k}{n_k'u_k'}=\frac{n_1u_1}{n_k'u_k}$

（2）无限远物体对应像高计算公式

无限远物体：用一束与光轴成一定夹角 $\omega$ 的平行光线表示。

$\omega$ ：从光轴转向光线，顺时针为正，逆时针为负

运用作图法，作过物方焦点，物方节点的两条特殊光线可以得到

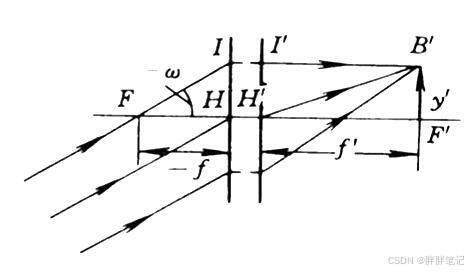
与像方焦面的交点是无限远轴外物点B的像点，由图知

$y'=HI=-f \cdot tg(-\omega)=f\cdot tg\omega$ ---无限远物体理想像高公式

如果位于空气中， $y'=f\cdot tg\omega$

（3）无限远的像对应的物高计算公式

无限远的轴外像点对应一束与光轴成一定夹角 $\omega'$ 的平行光线表示

运用作图法，作过像方焦点，像方节点的两条特殊光线可以得到

由图知 $y=H'I'=f' \cdot tg\omega'$ --无限远像对应理想物高公式

3、理想光学系统的组合

由两个已知的光学系统，求它们组合系统的成像性质

假定：两分系统的焦距分别为 $f_1,f_1'$ 和 $f_2,f_2'$ 。两分系统的相对位置用第一系统像方焦点 $F_1'$ 到第二系统的物方焦点 $F_2'$ 的距离 $\Delta$ 表示（以 $F_1'$ 为起点，计算到 $F_2'$ ，由左向右为正）。

1）焦距公式

（1）像方焦点 $F'$

根据作图法，先找出像方焦点 $F'$ 。对于第二光学系统 $F_1'$ 和 $F'$ 是一对共轭点。根据牛顿公式

$xx'=f_2f_2'$ ，其中 $x$ 是以 $F_2$ 为起点计算到 $F_1'$ 的距离， $x=-\Delta$ ， $x$ 是以 $F_2'$ 为起点计算到 $F'$ 的距离，用 $x_F'$ 表示。代入牛顿公式得 $x_F'=-\frac{f_2f_2'}{\Delta}$

（2）物方焦点 $F$

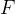
作图法找到物方焦点 $F$ 的位置。对于第一个光学系统， $F$ 和 $F_2$ 是一对共轭点。根据牛顿公式 $xx'=f_1f_1'$ ，其中 $x$ 是以 $F_1$ 为起点计算到 $F$ 的距离，用 $-x_F$ 表示， $x$ 是以 $F_1'$ 为起点计算到 $F_2$ 的距离，表示为 $x'=\Delta$ 。代入牛顿公式得 $x_F=-\frac{f_1f_1'}{\Delta}$

（3）焦距计算

焦点位置确定，求出焦距，主平面位置随之确定

平行光轴入射的光线与出射光线的延长线的交点为 $M'$ ，一定位于像方主平面上，过 $M'$ 作垂直于光轴的直线交光轴于 $H'$ 即为像方主点

由 $\Delta M'F'H' \sim \Delta I_2'H_2'F'$ ， $\Delta I_1'H_1'F_1' \sim \Delta I_2H_2F_1'$ 有

$\frac{M'H'}{I_2'H_2'}=\frac{H'F'}{H_2'F'}=\frac{-f'}{f_2'+x_F'}$ 和 $\frac{I_2H_2}{I_1'H_1'}=\frac{H_2F_1'}{H_1'F_1'}=\frac{-f_2+\Delta}{f_1'}$ ；由于 $I_2'H_2'=I_2H_2$ ，可得 $\frac{-f'}{f_2'+x_F'}=\frac{f_1'}{\Delta-f_2}$

由此可得像方焦距公式 $f'=\frac{-f_1'}{\Delta-f_2}(f_2'-\frac{f_2f_2'}{\Delta})=\frac{-f_1'}{\Delta-f_2} \cdot \frac{f_2'(\Delta-f_2)}{\Delta}=-\frac{f_1'f_2'}{\Delta}$ 。

设组合系统空间折射率为 $n_1$ ，子系统1、2之间为 $n_2$ ，像空间为 $n_3$ 。应用物方焦距和像方焦距的关系 $\frac{f'}{f}=-\frac{n'}{n}$ 得 $f=f'\frac{n_1}{n_3}=-\frac{f_1'f_2'}{\Delta}\frac{n_1}{n_3},f_1'=-f_1\frac{n_2}{n_1},f_2'=-f_2\frac{n_3}{n_2}$ ，

因此得出物方焦距公式 $f=\frac{f_1f_2}{\Delta}$ 。

有时也用另一种形式表示公式： $d$ 为两个系统主平面间的相对位置，以第一个系统像方主点 $H_1'$ 为起点，计算到第二个系统物方主点 $H_2$ ，由左向右为正。

$d=\Delta+f_1'-f_2$ 或者 $\Delta=d-f_1'+f_2$ 。

将其代入像方焦距公式得到 $\frac{1}{f'}=-\frac{\Delta}{f_1'f_2'}=\frac{1}{f_2'}-\frac{f_2}{f_1'f_2'}-\frac{d}{f_1'f_2'}$

再将 $\frac{f_2}{f_2'}=-\frac{n_2}{n_3}$ 代入上式并且同时乘以 $n_3$ 得焦距公式 $\frac{n_3}{f'}=\frac{n_2}{f_1'}+\frac{n_3}{f_2'}-\frac{n_3d}{f_1'f_2'}=-\frac{n_1}{f}$

如果两个系统位于同一种介质中， $n_1=n_2=n_3$ 得到 $\frac{1}{f'}=\frac{1}{f_1'}+\frac{1}{f_2'}-\frac{d}{f_1'f_2'}$

定义 $\varphi=\frac{1}{f'}$ 为光焦度，像方焦距得倒数 $\varphi=\varphi_1+\varphi_2-d\varphi_1\varphi_2$

当两个光学系统主平面间的距离d为零，即密接薄透镜组情况下 $\varphi=\varphi_1+\varphi_2$

2）光路计算公式

描一条理想的光路，找组合系统的焦点和主点，从而找出理想系统种任意物点的像点

（1）单个理想光学系统的光路计算公式

确定表示光线坐标 $\Rightarrow$ 画图并按照符号规则标注图形 $\Rightarrow$ 推导公式

光线位置用 $h,tgU,tgU'$ 表示， $h$ 是光线和主平面的交点到光轴的距离。

$A,A'$ 是一对共轭点，满足高斯公式 $\frac{f'}{l'}+\frac{f}{l}=1$ ，两边同时乘以h得到 $\frac{hf'}{l'}+\frac{hf}{l}=h$

同时有 $tgU=\frac{h}{l}$ ， $tgU'=\frac{h}{l'}$ ， $f=-\frac{n}{n'}f'$ ， $\varphi=\frac{1}{f'}$ 代入化简可得单个光学系统的光路计算公式 $n'tgU'-ntgU=n'h\varphi$

当 $n'=n=1$ 时， $tgU'-tgU=h\varphi$

（2）多个理想光学系统的光路计算公式

前一个光学系统的出射光线是后一个系统的入射光线，过度公式

$\begin{matrix}U_{i+1}=U_i' \\ h_{i+1}=h_i-d_itgU_i' \end{matrix}$

由此得到理想光学系统的光路计算公式

$\begin{matrix}n'tgU'-ntgU=n'h\varphi \\ U_{i+1}=U_i' \\ h_{i+1}=h_i-d_itgU_i' \end{matrix}$

理想光学系统的光路计算公式的应用

求组合系统的主平面，焦点位置

对于焦点和焦距，计算一条平行于光轴的光线，即 $U_1=0,h_1$ ，再利用理想光学系统光路计算公式计算出 $tgU_k'$ ，从而求出焦点位置 $l_F'=\frac{h_k}{tgU_k'}$ ，焦距 $f'=\frac{h_1}{tgU_k'}$ 。入射光线延延长线和出射光线反向延长线的交点一定在主平面上，由此可以确定主平面位置。

求像平面的位置和放大率

已知： $l_1,y_1$ ，如果给定 $h_1$ ，则 $tgU_1$ 就确定；给定 $U_1$ 确定，则 $h_1$ 确定。 $h_1$ 和 $tgU_1$ 为入射光线坐标，代入理想光学系统光路计算公式计算出 $tgU_k'$ ，进而求出焦点位置 $l_F'=\frac{h_k}{tgU_k'}$ ，利用垂轴放大率和角向放大率的关系可求出 $\beta=\frac{1}{\gamma}=\frac{tgu_1}{tgu_k'}$

计算光学零件的通光口径

在计算光学系统中各零件的口径大小时，经常用光路计算的方法，找出各零件上光线的投射高，从而确定口径

例：一个照明聚光灯使用直径为200mm的一个聚光镜，焦距 $f'=400mm$ ，要求照明距离5m远的一个3m直径的圆，问灯泡应安置在什么位置？

解：欲运用理想光学系统光路计算公式 $n'tgU'-ntgU=n'h\varphi$ ，先求出

$tg(-u')=\frac{1500-100}{5000}=\frac{7}{25}$

$h=100$ ， $\varphi=\frac{1}{400}$

所以 $tgu=-tgu'-h\varphi=-\frac{53}{100}$

$l=-\frac{100}{tg(-u)}=-188.68$

（3）单透镜的主平面和交点位置计算公式

单透镜是由两个折射球面构成，

已知： $r_1,r_2,d,n$ ，求：主平面位置和焦点位置

物方主平面： $l_H$ 以第一个折射球面顶点 $O_1$ 为起点到 $H$ ；像方主平面： $l_H'$ 以第二个折射球面顶点 $O_2$ 为起点到 $H'$

对于单透镜每个面运用单个球面的焦距公式 $f'=\frac{n'r}{n'-n}$ ， $f'=-\frac{nr}{n'-n}$ 有

$f_1'=\frac{nr_1}{n-1}$ ， $f_1=\frac{-r_1}{n-1}$ ， $f_2'=\frac{r_2}{1-n}$ ， $f_2=\frac{-nr_2}{1-n}$ ，

将其有理想光学系统组合的焦距公式 $\frac{n_3}{f'}=\frac{n_2}{f_1'}+\frac{n_3}{f_2'}-\frac{n_3d}{f_1'f_2'}=-\frac{n_1}{f}$ 化简得到单透镜的焦距公式

$\frac{1}{f'}=(n-1)(\frac{1}{r_1}-\frac{1}{r_2})-\frac{(n-1)d}{nr_1r_2}=-\frac{1}{f}$

由图知单透镜的物方焦距 $-f=-x_F-f_1+l_H$ ，像方焦距 $f'=x_F' + f_2' - l_H'$ ，因此

$l_H=x_F+f_1-f$ ， $l_H'=x_F' + f_2' -f'$ ，将 $x_F=-\frac{f_1f_1'}{\Delta}$ ， $x_F'=-\frac{f_2f_2'}{\Delta}$ 和焦距公式代入得

$l_H=\frac{-r_1d}{n(r_2-r_1)+(n-1)d}$ ， $l_H=\frac{-r_2d}{n(r_2-r_1)+(n-1)d}$

用a表示两个主平面之间的距离，从 $H$ 到 $H'$ ，有 $a=d-l_H+l_H'$ ，化简后有

$a=\frac{d(n-1)(r_2-r_1+d)}{n(r_2-r_1)+(n-1)d}$

绝大多数实际应用的透镜厚度和两半径只差相对较小，可简化为薄透镜公式

$\begin{matrix} \frac{1}{f'}=(n-1)(\frac{1}{r_1}-\frac{1}{r_2})=-\frac{1}{f} \\l_H=\frac{-r_1d}{n(r_2-r_1)} \\l_H=\frac{-r_2d}{n(r_2-r_1)} \\a=\frac{(n-1)d}{n} \end{matrix}$

各种透镜的形状及主平面位置

2048 AI社区

有“AI”的1024 = 2048，欢迎大家加入2048 AI社区

更多推荐

【信创-k8s】海光/兆芯+银河麒麟V10离线部署k8s1.31.8+kubesphere4.1.3

介于V4优秀的LuBan架构，核心组件非常少，资源占用也显著降低，同时带来众多功能和便利性。：使用海光3350/兆芯开先KX-5000芯片，麒麟V10 SP3操作系统，以及Containerd 1.7.13、Kubernetes v1.31.8、KubeSphere v4.1.3等软件版本。原创编写，详细记录了从环境准备到平台验证的完整流程，为信创环境下的Kubernetes与KubeSphere

2048 AI社区

从狂热到深耕：一个AI从业者的智能体创业心路历程

2048 AI社区

MCP：从被动响应到自主执行的自动化协议

AI正突破传统代码生成边界，向全流程智能调度演进。MCP（Model Context Protocol）作为开放协议，为AI与工具建立统一接口，实现跨模型、跨工具的复杂流程编排。其核心价值在于生态复用、安全可控和上下文感知，通过客户端-服务器架构让AI自主调用API完成从代码检查到性能优化的全流程。相比Function Call的单次调用，MCP支持多工具串联和本地数据处理，将重塑前端开发模式——

2048 AI社区

所有评论(0)

查看更多评论

胖胖笔记

@weixin_47567773

已为社区贡献3条内容

应用光学笔记02---共轴球面系统的物像关系

胖胖笔记

一、光学系统与成像的概念

1、光学系统

2、成像的概念

（1）透镜类型

（2）透镜作用---成像

二、共轴球面光学系统的物像关系式

1、单个折射球面光路计算公式

(1)符号规则

（2）光路计算公式

2、多个球面共轴系统---转面公式

3、近轴光学的物像基本式

1）近轴的定义

2）物像位置关系式

3）物像大小关系式

4）近轴光学公式的作用

三、共轴理想光学系统

1、理想像和理想光学系统

1）基本概念

2）理想成像

3）共轴理想光学系统成像性质：

2、共轴理想光学系统

1）主平面和基点

（1）放大率的一对共轭面称为主平面。

(2)无限远轴上物点和它所对应的像点----像方焦点

(3)无限远轴上像点和它所对应的物点----物方焦点

（4）焦距---主平面和焦点之间的距离

（5）共轴球面系统的主平面和焦点

2）共轴理想光学系统的物像关系式

（1）牛顿公式

（2）高斯公式

3） 光学系统的放大率

（1）垂轴放大率

（2）轴向放大率

（3）角放大率

4）物像空间不变式---拉格朗日-亥姆霍兹不变式

5）物方焦距和像方焦距得关系式---化简物像关系式

6）节平面和节点

7）物高和像高计算公式

3、理想光学系统的组合

1）焦距公式

（1）像方焦点

（2）物方焦点

（3）焦距计算

2）光路计算公式

（1）单个理想光学系统的光路计算公式

（2）多个理想光学系统的光路计算公式

（3）单透镜的主平面和交点位置计算公式

所有评论(0)

胖胖笔记

（1）放大率 $\beta=1$ 的一对共轭面称为主平面。

(2)无限远轴上物点和它所对应的像点 $F'$ ----像方焦点

(3)无限远轴上像点和它所对应的物点 $F$ ----物方焦点

3）光学系统的放大率

（1）垂轴放大率 $\beta=\frac{y'}{y}=-\frac{f}{x}=-\frac{x'}{f'}=-\frac{fl'}{f'l}$

（2）轴向放大率 $\alpha=\frac{dx'}{dx}=-\frac{x'}{x}=-\frac{fl'^2}{f'l^2}$

（3）角放大率 $\gamma=\frac{tgU'}{tgU}=\frac{l}{l'}$

（1）像方焦点 $F'$

（2）物方焦点 $F$