α算法是比较古老、原始和简单的流程发现算法，能够处理发现并发（concurrency）的能力，但在实践中不适用，因为存在一些问题（处理噪声、不频繁/不完整行为、复杂路由结构等）。这节介绍α算法，可以理解流程发现的内涵，并引出流程发现的挑战

一、α算法

1、基于日志的顺序关系

先引入基于日志的活动顺序关系。

定义1（基于日志的顺序关系，Log-based ordering relations）令是定义在活动集上的一个事件日志，即，令，那么

• 当且仅当存在一个行迹，有。
• 当且仅当且。
• 当且仅当且。
• 当且仅当且。

举个例子：，这个日志的顺序关系如下：

 可以用矩阵的形式来表示日志的活动顺序关系，称为足迹（footprint）。如上面日志的足迹为：

 通过活动的足迹我们可以确定它们的流程模式，如下表一些典型流程模式：

活动足迹	流程模式	对应Petri网
a→b	顺序（sequence）
a→b，a→c，b#c	XOR-split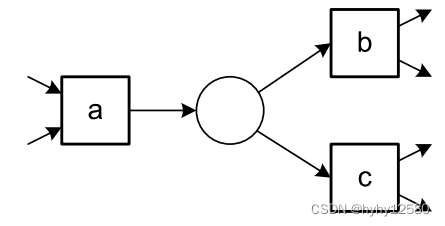
a→c，b→c，a#b	XOR-join
a→b，a→c，b||c	AND-split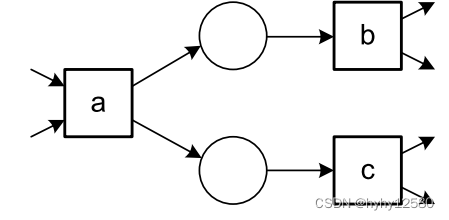
a→c，b→c，a||b	AND-join

2、α算法

基于日志的足迹，可以 通过α算法发现流程。

定义2（α算法）令是定义在活动集上的一个事件日志，定义为：

1. 确定变迁，对应事件日志的活动：
2. 起始变迁：
3. 终止变迁：
4. 确定库所的前集和后集：
5. 精简满足4的最大集合对(A，B)：
6. 确定库所，起始库所和终止库所：
7. 确定流关系：
8. 得到发现的Petri网：

举个例子：有日志如下：

根据算法 的八步求得各个集合：

 

 对应的Petri网的图为：

 

3、α算法的局限性

（1）冗余库所：日志在α算法下生成的Petri网如下图，p1和p2称为隐含库所（implicit places），移除它们并不会影响该Petri网的行为（行迹等价性）。这种问题不大，只是增加了发现图的复杂性，不过在模型很大时是很严重的。

 

 （2）无法处理短循环（short-loop，循环体为一个活动或两个活动）

日志发现的模型为：

 发现的模型为：

 

 主要原因是α算法会错误地将短循环中的活动判断为平行关系而不是循环，并且算法没有考虑平行关系。α+算法解决了这个问题。

（3）非自由选择流程结构（non-free choice process constructs）导致的非局部依赖（non-local dependencies）

 日志发现模型没有下图的p1和p2库所，α算法无法得到这种非局部依赖，这导致发现的模型会运行不在日志中的更多行为。

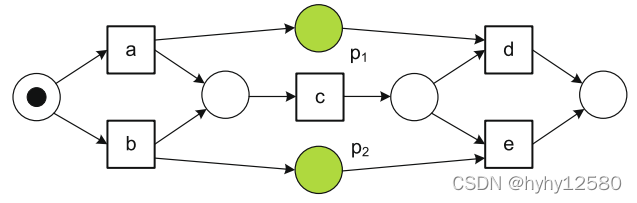
（4）没有把（依赖）频数/频率考虑进去。

二、挑战