工具系列:时间序列预测工具Dart介绍_静态协变量
将静态协变量定义为一个,其中列代表静态变量,行代表它们将被添加到的单变量/多变量TimeSeries的组件。行数必须为1或等于series的组件数。对于具有多个组件的多元时间序列,使用单行静态协变量数据框,静态协变量将被全局映射到所有组件。# 创建一个包含连续和分类静态协变量的数据框,其中包含一行数据# 创建一个包含多个组件的多元静态协变量数据框,注意行数与`series`的组件数相匹配cont
文章目录
# 导入fix_pythonpath_if_working_locally函数
from utils import fix_pythonpath_if_working_locally
# 调用fix_pythonpath_if_working_locally函数,用于修复本地工作时的Python路径问题
fix_pythonpath_if_working_locally()
# 加载autoreload扩展,可以在代码修改后自动重新加载模块
%load_ext autoreload
# 设置autoreload的模式为2,即在代码修改后自动重新加载模块
%autoreload 2
# 设置matplotlib的显示模式为inline,即将绘制的图像直接显示在notebook中
%matplotlib inline
# 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 导入时间序列库
from darts import TimeSeries
# 忽略警告信息
import warnings
warnings.filterwarnings("ignore")
# 禁用日志记录
import logging
logging.disable(logging.CRITICAL)
静态协变量是时间序列的特征/常量,它们不随时间变化而改变。在处理多个时间序列时,静态协变量可以帮助特定的模型改善预测。Darts的模型只会考虑嵌入在目标序列(我们想要预测未来值的序列)中的静态协变量,而不考虑过去和/或未来的协变量(外部数据)。
在本教程中,我们将讨论:
- 如何定义静态协变量(数值和/或分类)
- 如何将静态协变量添加到现有的目标序列中
- 如何在TimeSeries创建时添加静态协变量
- 如何使用TimeSeries.from_group_dataframe()自动提取嵌入静态协变量的TimeSeries
- 如何缩放/转换/编码嵌入在您的序列中的静态协变量
- 如何在Darts的模型中使用静态协变量
我们从生成一个具有三个组件["comp1", "comp2", "comp3"]的多变量时间序列开始。
# 导入必要的库已经省略
# 设置随机数种子,保证每次运行结果一致
np.random.seed(0)
# 生成一个时间序列,包含10个时间点,每个时间点包含3个随机数,列名分别为"comp1", "comp2", "comp3"
series = TimeSeries.from_times_and_values(
times=pd.date_range(start="2020-01-01", periods=10, freq="h"),
values=np.random.random((10, 3)),
columns=["comp1", "comp2", "comp3"],
)
# 绘制时间序列的图形
series.plot()

1. 定义静态协变量
将静态协变量定义为一个pd.DataFrame,其中列代表静态变量,行代表它们将被添加到的单变量/多变量TimeSeries的组件。
- 行数必须为1或等于
series的组件数。 - 对于具有多个组件的多元时间序列,使用单行静态协变量数据框,静态协变量将被全局映射到所有组件。
# 创建一个包含连续和分类静态协变量的数据框,其中包含一行数据
static_covs_single = pd.DataFrame(data={"cont": [0], "cat": ["a"]})
print(static_covs_single)
# 创建一个包含多个组件的多元静态协变量数据框,注意行数与`series`的组件数相匹配
static_covs_multi = pd.DataFrame(data={"cont": [0, 2, 1], "cat": ["a", "c", "b"]})
print(static_covs_multi)
cont cat
0 0 a
cont cat
0 0 a
1 2 c
2 1 b
2. 给现有的TimeSeries添加静态协变量
使用方法with_static_covariates()从现有的TimeSeries创建一个新的系列,并添加静态协变量(请参见此处的文档)
- 具有多元
series的单行静态协变量将创建“global_components”,这些组件将映射到所有组件 - 具有多元
series的多行静态协变量将映射到series的组件名称(请参见静态协变量索引/行名称)
# 确保series的static_covariates属性为None
assert series.static_covariates is None
# 将static_covs_single作为静态协变量添加到series中,并将结果赋值给series_single
series_single = series.with_static_covariates(static_covs_single)
print("Single row static covarites with multivariate `series`")
print(series_single.static_covariates)
# 将static_covs_multi作为静态协变量添加到series中,并将结果赋值给series_multi
print("\nMulti row static covarites with multivariate `series`")
print(series_multi.static_covariates)
Single row static covarites with multivariate `series`
static_covariates cont cat
global_components 0.0 a
Multi row static covarites with multivariate `series`
static_covariates cont cat
component
comp1 0.0 a
comp2 2.0 c
comp3 1.0 b
3. 在TimeSeries构建时添加静态协变量
在大多数TimeSeries.from_*()方法中,也可以直接使用参数static_covariates添加静态协变量。
# 创建一个时间序列对象
series = TimeSeries.from_values(
values=np.random.random((10, 3)), # 生成一个10行3列的随机数矩阵,作为时间序列的值
columns=["comp1", "comp2", "comp3"], # 设置时间序列的列名为comp1, comp2, comp3
static_covariates=static_covs_multi, # 添加连续和分类的静态协变量
)
# 打印时间序列对象的静态协变量
print(series.static_covariates)
static_covariates cont cat
component
comp1 0.0 a
comp2 2.0 c
comp3 1.0 b
使用静态协变量与多个时间序列
只有在跨多个时间序列使用时,静态协变量才真正有用。按照惯例,静态协变量的布局(pd.DataFrame列,索引)必须对所有系列相同。
# 定义了一个名为series的时间序列对象
# 时间序列对象是由pandas库中的TimeSeries类创建的
# 这个时间序列对象包含了一些时间序列数据和一些时间序列数据的元数据
series = TimeSeries(data, time_col="time", value_cols=["value"], freq="D")
# 给第一个时间序列对象添加了一个静态协变量
# 静态协变量是指在时间序列的整个时间范围内不变的协变量
# 这个静态协变量是一个名为var1的变量,值为0.5,对应的ID为SERIES1
first_series = series.with_static_covariates(pd.DataFrame(data={"ID": ["SERIES1"], "var1": [0.5]}))
# 给第二个时间序列对象添加了一个静态协变量
# 这个静态协变量是一个名为var1的变量,值为0.75,对应的ID为SERIES2
second_series = series.with_static_covariates(pd.DataFrame(data={"ID": ["SERIES2"], "var1": [0.75]}))
# 打印出多个时间序列对象的静态协变量
print("Valid static covariates for multiple series")
print(first_series.static_covariates)
print(second_series.static_covariates)
# 将第一个和第二个时间序列对象组成一个列表
series_multi = [first_series, second_series]
Valid static covariates for multiple series
static_covariates ID var1
global_components SERIES1 0.5
static_covariates ID var1
global_components SERIES2 0.75
4. 使用 from_group_dataframe() 从 DataFrame 中按组提取时间序列列表
如果您的 DataFrame 包含多个垂直堆叠的时间序列,您可以使用 TimeSeries.from_group_dataframe()(请参见文档此处)将它们提取为 TimeSeries 实例列表。这需要一个列或列列表,用于按其分组 DataFrame(参数 group_cols)。group_cols 将自动添加为静态协变量到各个系列。其他列可以使用参数 static_cols 作为静态协变量。
在下面的示例中,我们生成一个包含两个不同时间序列(重叠/重复日期)“SERIES1”和“SERIES2”的数据的 DataFrame,并使用 from_group_dataframe() 提取 TimeSeries。
# 生成一个DataFrame示例
df = pd.DataFrame(
data={
"dates": [
"2020-01-01",
"2020-01-02",
"2020-01-03",
"2020-01-01",
"2020-01-02",
"2020-01-03",
],
"comp1": np.random.random((6,)),
"comp2": np.random.random((6,)),
"comp3": np.random.random((6,)),
"ID": ["SERIES1", "SERIES1", "SERIES1", "SERIES2", "SERIES2", "SERIES2"],
"var1": [0.5, 0.5, 0.5, 0.75, 0.75, 0.75],
}
)
# 打印输入的DataFrame
print("输入的DataFrame")
print(df)
# 使用TimeSeries.from_group_dataframe从DataFrame中提取时间序列
series_multi = TimeSeries.from_group_dataframe(
df,
time_col="dates",
group_cols="ID", # 通过将`df`按`group_cols`分组来提取各个时间序列
static_cols=[
"var1"
], # 作为静态协变量提取这些额外的列(不进行分组)
value_cols=[
"comp1",
"comp2",
"comp3",
], # 可选地,指定时间变化的列
)
# 打印从输入DataFrame中提取的时间序列的数量
print(f"\n从输入的DataFrame中提取了{len(series_multi)}个时间序列")
for i, ts in enumerate(series_multi):
# 打印第i个时间序列的静态协变量
print(f"第{i}个时间序列的静态协变量")
print(ts.static_covariates)
# 绘制"comp1"列的时间序列
ts["comp1"].plot(label=f"comp1_series_{i}")
Input DataFrame
dates comp1 comp2 comp3 ID var1
0 2020-01-01 0.158970 0.820993 0.976761 SERIES1 0.50
1 2020-01-02 0.110375 0.097101 0.604846 SERIES1 0.50
2 2020-01-03 0.656330 0.837945 0.739264 SERIES1 0.50
3 2020-01-01 0.138183 0.096098 0.039188 SERIES2 0.75
4 2020-01-02 0.196582 0.976459 0.282807 SERIES2 0.75
5 2020-01-03 0.368725 0.468651 0.120197 SERIES2 0.75
2 series were extracted from the input DataFrame
Static covariates of series 0
static_covariates ID var1
global_components SERIES1 0.5
Static covariates of series 1
static_covariates ID var1
global_components SERIES2 0.75

5. 缩放/编码/转换静态协变量数据
可能需要缩放数字静态协变量或编码分类静态协变量,因为并非所有模型都能处理非数字静态协变量。
使用StaticCovariatesTransformer(请参见此处的文档[https://unit8co.github.io/darts/generated_api/darts.dataprocessing.transformers.static_covariates_transformer.html#staticcovariatestransformer])来缩放/转换静态协变量。默认情况下,它使用MinMaxScaler来缩放数字数据,使用OrdinalEncoder来编码分类数据。
数字和分类转换器都将在传递给StaticCovariatesTransformer.fit()的所有时间序列的静态协变量数据上进行全局拟合。
# 导入StaticCovariatesTransformer类
from darts.dataprocessing.transformers import StaticCovariatesTransformer
# 创建StaticCovariatesTransformer对象
transformer = StaticCovariatesTransformer()
# 对series_multi进行拟合和转换
series_transformed = transformer.fit_transform(series_multi)
# 遍历series_multi和series_transformed,输出原始序列和转换后的序列的静态协变量
for i, (ts, ts_scaled) in enumerate(zip(series_multi, series_transformed)):
print(f"Original series {i}") # 输出原始序列的编号
print(ts.static_covariates) # 输出原始序列的静态协变量
print(f"Transformed series {i}") # 输出转换后的序列的编号
print(ts_scaled.static_covariates) # 输出转换后的序列的静态协变量
print("") # 输出空行,方便阅读
Original series 0
static_covariates ID var1
global_components SERIES1 0.5
Transformed series 0
static_covariates ID var1
global_components 0.0 0.0
Original series 1
static_covariates ID var1
global_components SERIES2 0.75
Transformed series 1
static_covariates ID var1
global_components 1.0 1.0
6. 使用TFTModel和静态协变量的预测示例
现在让我们看看在预测问题中添加静态协变量是否可以提高预测准确性。
我们将使用支持数值和分类静态协变量的TFTModel。
# 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pytorch_lightning.callbacks import TQDMProgressBar
# 导入darts库中的相关模块
from darts import TimeSeries
from darts.models import TFTModel
from darts.utils import timeseries_generation as tg
from darts.dataprocessing.transformers import StaticCovariatesTransformer
from darts.metrics import rmse
6.1 实验设置
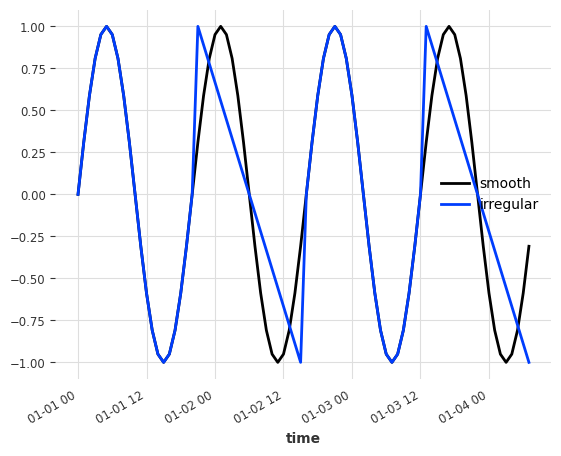
对于我们的实验,我们生成了两个时间序列:一个完全的正弦波序列(标签=平滑)和一个带有每隔一个周期的一些不规则性的正弦波序列(标签=不规则,参见第2和第4个周期的斜坡)。
# 设置周期为20
period = 20
# 生成正弦函数时间序列,长度为4倍周期,频率为1/周期,列名为"smooth",时间单位为小时
sine_series = tg.sine_timeseries(
length=4 * period, value_frequency=1 / period, column_name="smooth", freq="h"
)
# 获取正弦函数时间序列的值
sine_vals = sine_series.values()
# 生成线性序列,从1到-1,共19个数,然后将其转换为列向量
linear_vals = np.expand_dims(np.linspace(1, -1, num=19), -1)
# 将线性序列的值插入到正弦函数时间序列的第21到40个值和第61到80个值之间
sine_vals[21:40] = linear_vals
sine_vals[61:80] = linear_vals
# 生成新的时间序列,值为插入线性序列后的正弦函数时间序列的值,时间索引与原正弦函数时间序列相同,列名为"irregular"
irregular_series = TimeSeries.from_times_and_values(
values=sine_vals, times=sine_series.time_index, columns=["irregular"]
)
# 绘制原正弦函数时间序列和插入线性序列后的时间序列
sine_series.plot()
irregular_series.plot()
我们将使用三种不同的设置进行训练和评估:
- 没有静态协变量的拟合/预测
- 具有二进制(数值)静态协变量的拟合/预测
- 具有分类静态协变量的拟合/预测
对于每个设置,我们将在两个序列上训练模型,然后仅使用第三个周期(对于两个序列都是正弦波)来预测第四个周期(对于“平滑”是正弦波,对于“不规则”是斜坡)。
我们希望的是,没有静态协变量的模型表现比其他模型差。非静态模型不应该能够识别predict()中使用的基础序列是“平滑”序列还是“不规则”序列,因为它只得到正弦波曲线作为输入(第三个周期)。这应该会导致预测结果在平滑和不规则序列之间(通过训练期间最小化全局损失学习)。
现在静态协变量可以真正帮助我们了。例如,我们可以通过静态协变量将曲线类型的数据嵌入到目标序列中。有了这些信息,我们期望模型能够生成更好的预测。
首先,我们创建一些辅助函数,将相同的实验条件应用于所有模型。
# 定义函数test_case,用于模型训练、预测和绘图
# 参数:
# - model: 模型对象,用于训练和预测
# - train_series: 训练数据序列,用于模型训练
# - predict_series: 预测数据序列,用于模型预测
# 返回值:
# - preds: 预测结果序列
def test_case(model, train_series, predict_series):
# 模型训练
model.fit(train_series)
# 模型预测
preds = model.predict(n=int(period / 2), num_samples=250, series=predict_series)
# 遍历训练数据序列和预测结果序列
for ts, ps in zip(train_series, preds):
# 绘制训练数据序列
ts.plot()
# 绘制预测结果序列
ps.plot()
# 显示绘图
plt.show()
# 返回预测结果序列
return preds
# 定义函数get_model_params,用于生成模型参数
# 返回值:
# - 模型参数字典
def get_model_params():
# 生成模型参数字典,并使用新的Progress Bar对象
return {
"input_chunk_length": int(period / 2),
"output_chunk_length": int(period / 2),
"add_encoders": {
"datetime_attribute": {"future": ["hour"]}
}, # TFTModel需要未来输入,使用此参数可以不提供任何未来协变量
"random_state": 42,
"n_epochs": 150,
"pl_trainer_kwargs": {
"callbacks": [TQDMProgressBar(refresh_rate=4)],
},
}
6.2 不使用静态协变量进行预测
让我们首先训练一个没有任何静态协变量的模型。
# 定义训练数据集
train_series = [sine_series, irregular_series]
# 遍历训练数据集,检查是否有静态协变量
for series in train_series:
assert not series.has_static_covariates
# 获取模型参数并创建TFT模型
model = TFTModel(**get_model_params())
# 对模型进行测试,传入训练数据集和预测数据集
preds = test_case(
model,
train_series,
predict_series=[series[:60] for series in train_series],
)
Training: 0it [00:00, ?it/s]
Predicting: 0it [00:00, ?it/s]


从图中可以看出,预测开始于第3个周期之后(~2022年01月03日-12:00)。预测的输入是最后的input_chunk_length=10个值,这两个序列(正弦波)是相同的。
正如预期的那样,模型无法确定基础预测序列的类型(平滑或不规则),并为两者生成了类似正弦波的预测。
6.3 使用0/1二进制静态协变量(数值)进行预测
现在让我们重复实验,但这次我们将曲线类型的信息作为一个名为"curve_type"的二进制(数值)静态协变量添加进去。
# 创建一个包含静态协变量的正弦序列
sine_series_st_bin = sine_series.with_static_covariates(
pd.DataFrame(data={"curve_type": [1]})
)
# 创建一个包含静态协变量的不规则序列
irregular_series_st_bin = irregular_series.with_static_covariates(
pd.DataFrame(data={"curve_type": [0]})
)
# 创建一个训练序列列表,包含了上述两个序列
train_series = [sine_series_st_bin, irregular_series_st_bin]
# 遍历训练序列列表
for series in train_series:
# 打印序列的静态协变量
print(series.static_covariates)
# 使用给定的模型参数创建一个TFT模型
model = TFTModel(**get_model_params())
# 对训练序列进行测试,并预测未来的序列
preds_st_bin = test_case(
model,
train_series,
predict_series=[series[:60] for series in train_series],
)
static_covariates curve_type
component
smooth 1.0
static_covariates curve_type
component
irregular 0.0
Training: 0it [00:00, ?it/s]
Predicting: 0it [00:00, ?it/s]

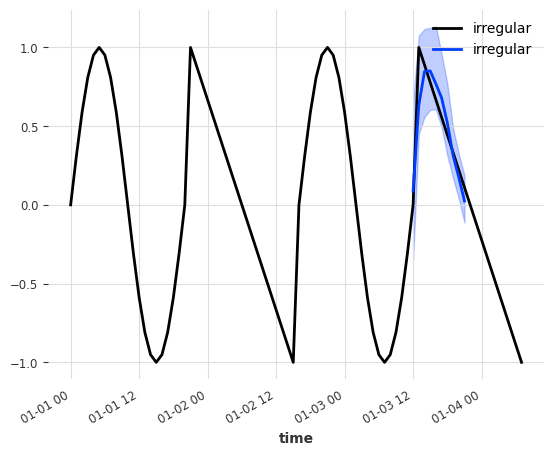
那看起来已经好多了!模型能够从二进制静态协变量特征中识别曲线类型/类别。
6.4 使用分类静态协变量进行预测
上一个实验已经展示了很有前途的结果。那么为什么不仅使用二进制特征来处理分类数据呢?
虽然对于我们的两个时间序列来说可能效果不错,但如果我们有更多的曲线类型,我们需要将特征进行独热编码,将每个类别转换为二进制变量。对于大量类别,这会导致特征/预测器数量增加,多重共线性可能会降低模型的预测准确性。
作为最后一个实验,让我们将曲线类型作为分类特征。TFTModel 为分类特征学习了一个嵌入。Darts 的 TorchForecastingModels(如 TFTModel)仅支持数值数据。在训练之前,我们需要使用 StaticCovariatesTransformer(参见第 5 节)将 "curve_type" 转换为整数值特征。
# 导入必要的库
import pandas as pd
# 创建带有静态协变量的正弦序列
sine_series_st_cat = sine_series.with_static_covariates(
pd.DataFrame(data={"curve_type": ["smooth"]})
)
# 创建带有静态协变量的非平滑序列
irregular_series_st_cat = irregular_series.with_static_covariates(
pd.DataFrame(data={"curve_type": ["non_smooth"]})
)
# 将两个序列放入训练序列列表中
train_series = [sine_series_st_cat, irregular_series_st_cat]
# 打印编码前的静态协变量
print("编码前的静态协变量:")
print(train_series[0].static_covariates)
# 使用StaticCovariatesTransformer将分类静态协变量编码为数值数据
scaler = StaticCovariatesTransformer()
train_series = scaler.fit_transform(train_series)
# 打印编码后的静态协变量
print("\n编码后的静态协变量:")
print(train_series[0].static_covariates)
Static covariates before encoding:
static_covariates curve_type
component
smooth smooth
Static covariates after encoding:
static_covariates curve_type
component
smooth 1.0
现在我们需要做的就是告诉TFTModel,"curve_type"是一个需要进行嵌入的分类变量。
我们可以通过模型参数categorical_embedding_sizes来实现,它是一个字典,格式为:{特征名称: (类别数量, 嵌入大小)}。
# 定义分类变量的类别数和嵌入向量的大小
n_categories = 2 # "smooth" 和 "non_smooth" 两种类别
embedding_size = 2 # 将分类变量嵌入到大小为2的数值向量中
categorical_embedding_sizes = {"curve_type": (n_categories, embedding_size)}
# 使用TFTModel类创建模型,传入分类变量的嵌入向量大小和其他参数
model = TFTModel(
categorical_embedding_sizes=categorical_embedding_sizes, **get_model_params()
)
# 对训练数据进行测试,预测序列为每个训练序列的前60个数据点
preds_st_cat = test_case(
model,
train_series,
predict_series=[series[:60] for series in train_series],
)
Training: 0it [00:00, ?it/s]
Predicting: 0it [00:00, ?it/s]


不错,这似乎也起作用了!作为最后一步,让我们看看模型相互之间的表现如何。
# 使用zip函数将四个列表进行循环迭代,分别为train_series, preds, preds_st_bin, preds_st_cat
for series, ps_no_st, ps_st_bin, ps_st_cat in zip(train_series, preds, preds_st_bin, preds_st_cat):
# 绘制series列表中最后40个元素的折线图,作为目标值的图像
series[-40:].plot(label="target")
# 计算ps_no_st的0.5分位数,并绘制折线图
ps_no_st.quantile(0.5).plot(label="no static covs")
# 计算ps_st_bin的0.5分位数,并绘制折线图
ps_st_bin.quantile(0.5).plot(label="binary static covs")
# 计算ps_st_cat的0.5分位数,并绘制折线图
ps_st_cat.quantile(0.5).plot(label="categorical static covs")
# 显示图像
plt.show()
# 输出"Metric"
print("Metric")
# 创建一个DataFrame,包含三个列名为"no st", "bin st", "cat st"的列,以及对应的RMSE值
print(
pd.DataFrame(
{
name: [rmse(series, ps)]
for name, ps in zip(
["no st", "bin st", "cat st"], [ps_no_st, ps_st_bin, ps_st_cat]
)
},
index=["RMSE"],
)
)

Metric
no st bin st cat st
RMSE 0.16352 0.042527 0.050242

Metric
no st bin st cat st
RMSE 0.289051 0.138122 0.138631
这些是很棒的结果!使用静态协变量的两种方法,相对于基准线,两个系列的RMSE都减少了一半以上!
请注意,我们只使用了一个静态协变量特征,但您可以使用尽可能多的特征,包括数据类型的混合(数字和分类)。
更多推荐
 已为社区贡献95条内容
已为社区贡献95条内容







所有评论(0)